6.Редуцирование масс.

Редуцирование масс – это приведение масс с уровня подкрановых балок на уровень покрытия в бескрановых рамах.

Для этого необходимо составить матрицу жесткости и матрицу масс для поперечной рамы.

Составление матрицы жесткости промежуточной и торцевой рамы

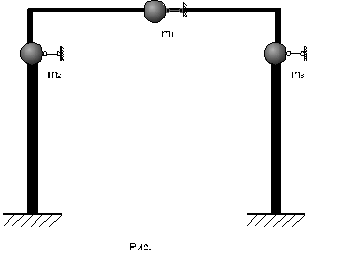
Матрица масс промежуточной рамы.

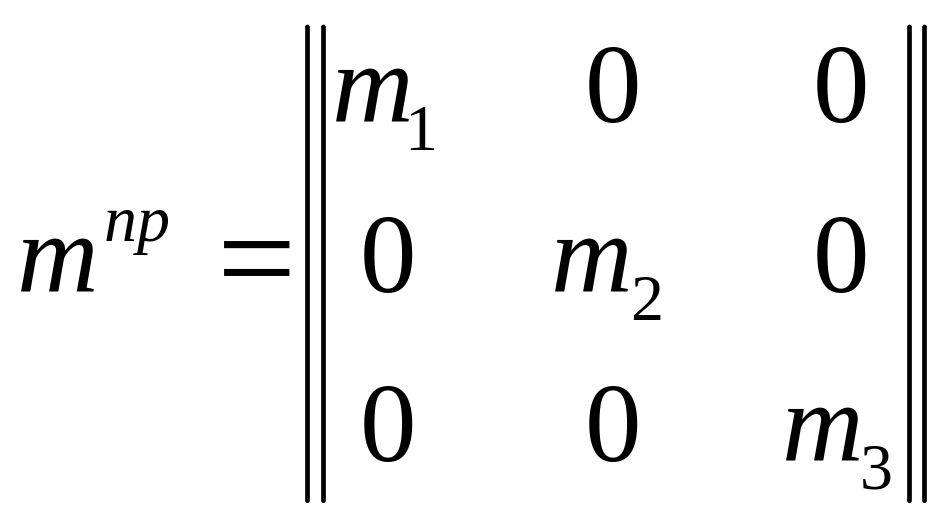
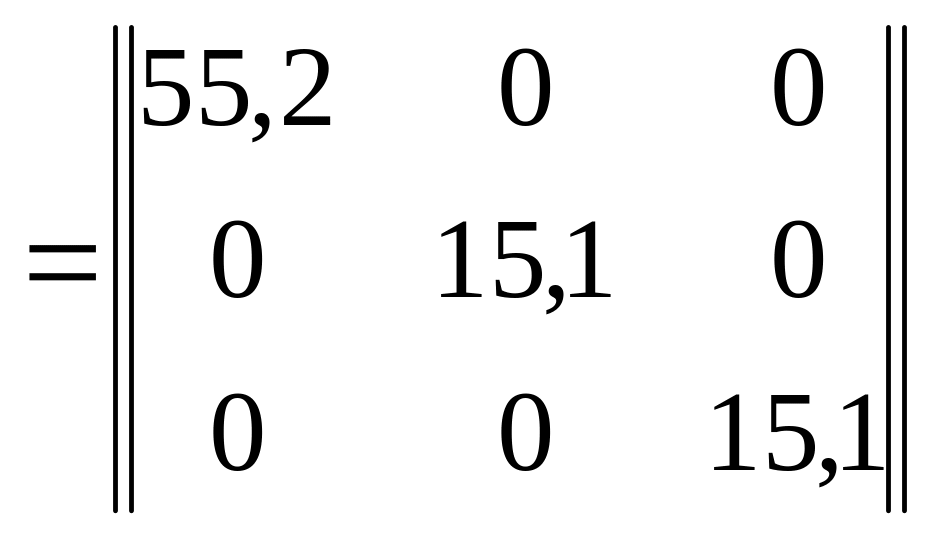
Матрица масс торцевой рамы имеет вид

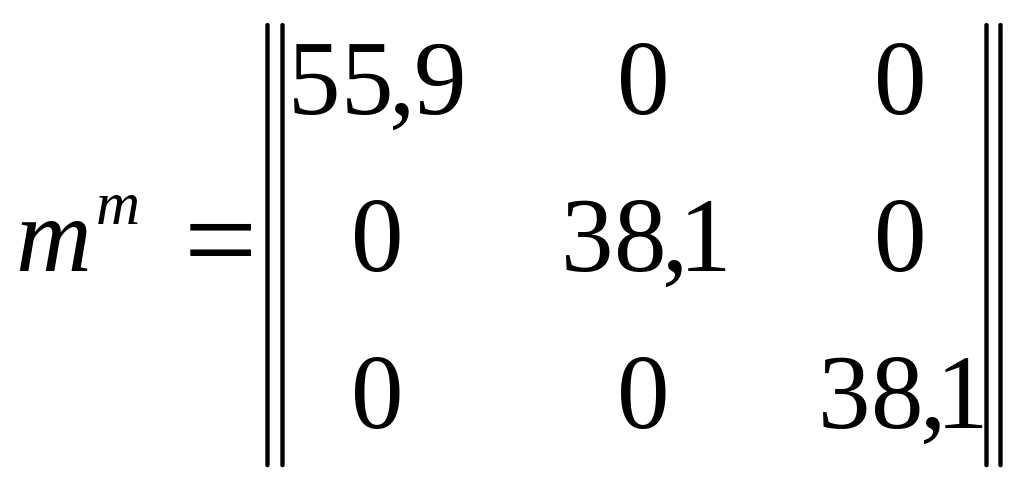
Редуцирование матрицы масс

7.Составление матрицы масс

Общий вид матрицы масс:

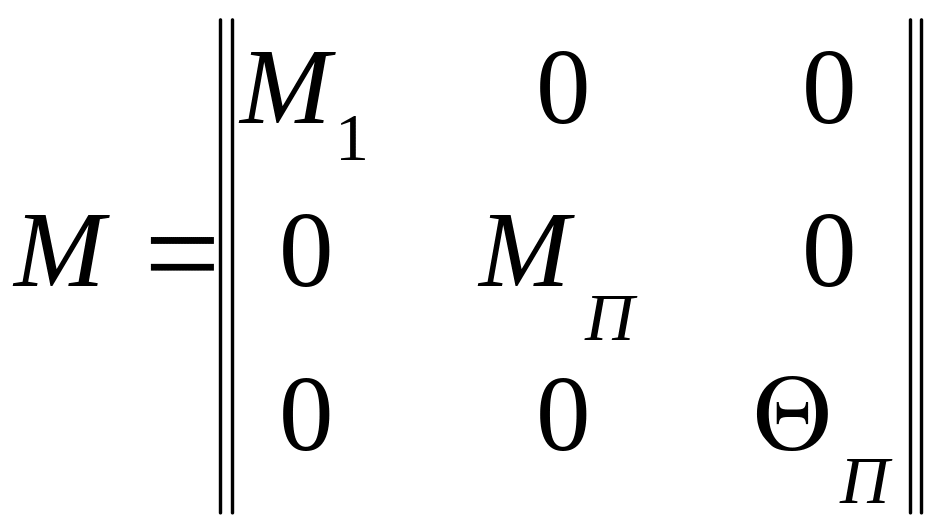, где

М₁ = 2·М₂ + m_кр + m_тел + m_гр, где

m_кр + m_тел = 1250кН=125 т – вес крана с тележкой;

m_гр = 100 т – масса груза (грузоподъёмность)

М₁= 255,9+ 100+ 125 = 337 (т)

Масса, сосредоточенная в центре масс покрытия:

М_П = 2 m_1r^т + М₄ + m_1r^пр (n – 3), где

n = 25 – кол-во рам

М_П = 271,1+ 38,1+(25- 3)61,2 = 1527(т)

Момент инерции диска покрытия:

_П = (М_П/12)(L² + К²) = (1527/12)(24² + 144²) = 2711419 (тм²)

Матрица масс имеет вид:

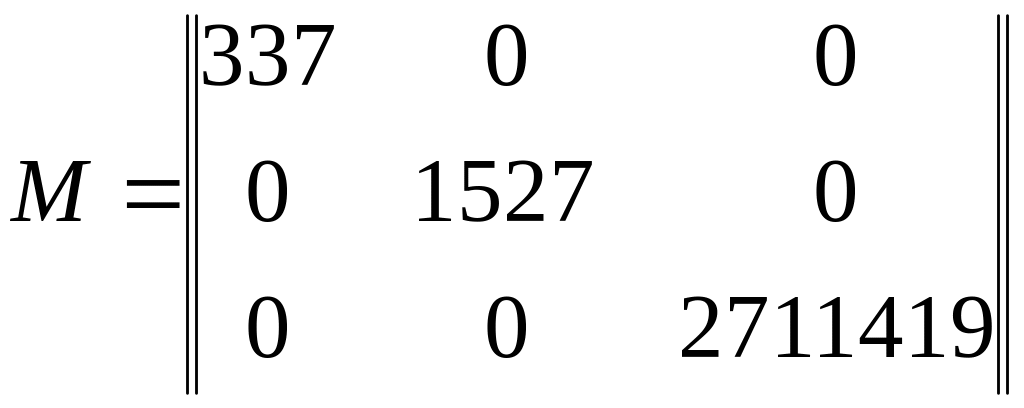
8.Определение величины крановой нагрузки

При пространственной расчетной схеме расчетная крановая нагрузка определяется следующим образом:

• нормативная нагрузка, возникающая от торможения крановой тележки на 1-ом колесе

Тⁿ = f  (G_т + Qg) / n₀, где

f – коэффициент трения, зависящий от типа подвеса груза;

G_т – вес тележки, кН;

Q – грузоподъемность крана, т;

g = 9,81– ускорение свободного падения;

n₀ – число колес с одной стороны мостового крана.

крановая нагрузка от торможения тележки, действующая на колонну

Т = Тⁿ  n  _н  n_s  у, где

n=1,1 – коэффициент перегрузки;

_н=0,95 – коэффициент надежности по назначению;

n_с=1 – коэффициент сочетания;

у – сумма ординат линий влияния тормозной нагрузки.

При грузоподъемности крана 100т и пролете 24 м принимаем крановое оборудование с параметрами:

Нормативное усилие от колеса F_к=450 кН.

Сумма ординат линии влияния y=2,62

Вес тележки G_т=410 кН.

T_к^н=0,05(9,81Q+G_т)/n₀=0,05 (9,81100+410)/4=17,4 кН.

Сила Т : T=_нnn_cT_к^н y=0,951,1117,42,62=48 кН

9.Определение смещения расчетных точек

При динамическом расчете одноэтажного промышленного здания с жестким в своей плоскости покрытием используется преобразованная расчетная схема, в которой ОПЗ путем приема редуцирования представляется в виде двухмассовой системы. Дискретные массы путем редуцирования приводятся в точку, расположенную в уровне покрытия и точку, расположенную в уровне тормозных конструкций.

К рановую нагрузку при торможении тележки рассматривают по графику

Нагрузка носит почти ударный ха-

рактер. При торможении возникают

колебания.

0,02 1,99 2,0 t ,c

Дифференциальное уравнение, описывающее колебания ОПЗ под действием динамической нагрузки:

||M||{q`(t)} + ||X||{q``(t)} + ||C||{q(t)} = {P(t)} (1), где

||M|| - матрица инерционных параметров здания;

||X|| = 2||M|| - матрица коэффициентов сопротивления, где

 - коэффициент демпфирования, определяемый по формуле:

 = w_ / 21+(/2)

( - логарифмический декремент затухания, равный для стальных конструкций 0,3, w_ - собственная частота колебаний по -той форме)

||C|| - матрица жесткости здания;

{q(t)} – вектор смещения расчетных точек;

{P(t)} – вектор динамической крановой нагрузки.

Для решения уравнения (1) используется метод разложения по главным формам колебаний, согласно которому смещение расчетных точек представляется в виде суммарных амплитудных значений смещений по главным формам колебания.

Смещение представлено интегралом Дюамеля:

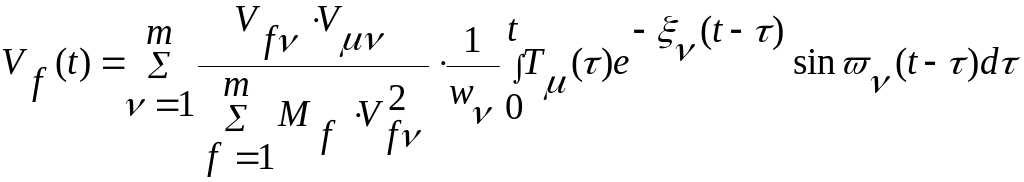, где

f – номер расчетной точки;

  номер формы колебания;

V_f, V_  амплитудные значения смещений расчетных точек f и  при -то форме колебания;

  расчетная точка, где приложена динамическая крановая нагрузка

_f  масса расчетной точки f;

_  собственная частота колебания с учетом затухания

_ = _² + n_²

  текущая функция t;

_(  значение нагрузки от торможения крановой тележки в расчетной точке  в момент времени ;

_  крановая нагрузка, приложенная в расчетной точке .