11.Эластичность функции спроса и предложения.

Э ластичность ф-ции предл-я. Рассмотрим график ф-ции предл-я p=p(x) и эластичность E_p в точке x=x₀.

Эластичность E_p в точке x=x₁:

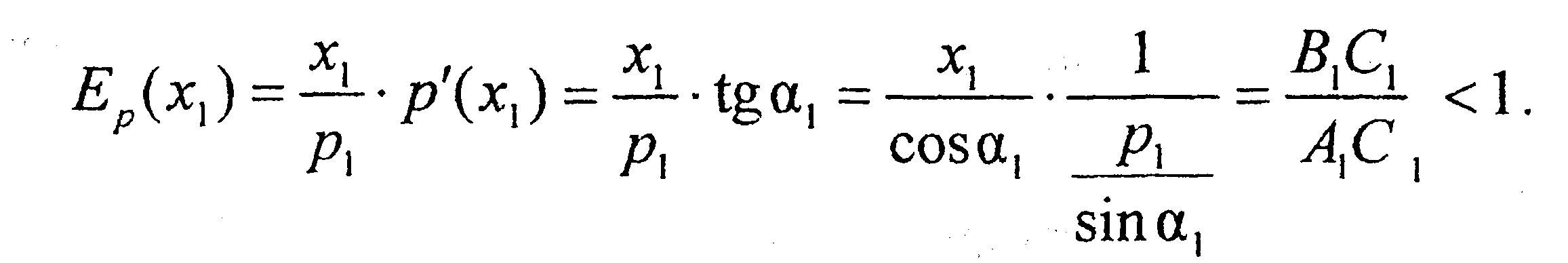
Т.о. с учетом геом. смысла производной геом. смысл эл-ти – отн-е длины касательной от точки касания до точки пересечения касательной с осью ординат к длине касательной от точки пересечения с осью абсцисс.Из привед. примеров геом. смысла, эластичн-ти ф-ции предл-я след-ет, что С эк. точки зрения предл-е счит. эластичным (Е_р>I), если изм. рын. цены товара на опред. вел. в % влечет за собой более значит. в % изм-е объема пр-ва и предложения данного товара.Е_p=1 соотв. случаю, когда изм-е рын. цены товара на опред. величи­ну в % влечет за собой такое же в % изм-е объема пр-ва и предл-я товара. Неэластичным считается предл-е, если изм-е рын. цены на 1% вызывает изм-е объема пр-ва менее чем на 1% (0 <Е_р<1).

Эл-ть ф-ции спроса. Рассмотрим грфик ф-ции спроса x= x(p). где x(p)- спрос, ap- цена. Из гр-ка след., что чем выше цена p, тем меньше спрос x=x(p).Согласно геом. смыслу пр-ной:

Аналогично, как для ф-ции предл-я, можно показать, что эл-ть ф-ции спроса находится в пределах , поскольку перед отн-ем длин стоит знак минус. Различ. след. виды эл-ти спроса по цене: эл-ть единичная, эластичный спрос, неэластичный спрос, совершенно эла­стичный спрос, совершенно неэластичный спрос.Под единичной эл-тью понимают случай, когда Е_х=-1то есть когда на каждый % изм-я цены спрос количественно изм-ся на 1 %. При эл. спросе (Е_x<-1) величина спроса изм-ся в большей мере, чем цена, и, наоборот, при неэластичном спро­се (-1 <Е_х<0). Совершенно эластичный спрос определяет сит-ю, при кот. величина спроса бесконечно изм-ся - при малом измене­нии цены (Е_х=--00). Совершенно неэластичный спрос (Е_х= 0) обуслов­ливается ситуацией, когда величина спроса не изменяется при любом изменении цены.Необходимо заметить, что величина выручки будет определяться ви­дом эл-ти и характером изм-я цены. В табл. представлены изменения выручки в зав-ти oт знака изм-я цены и вида эл-ти спроса.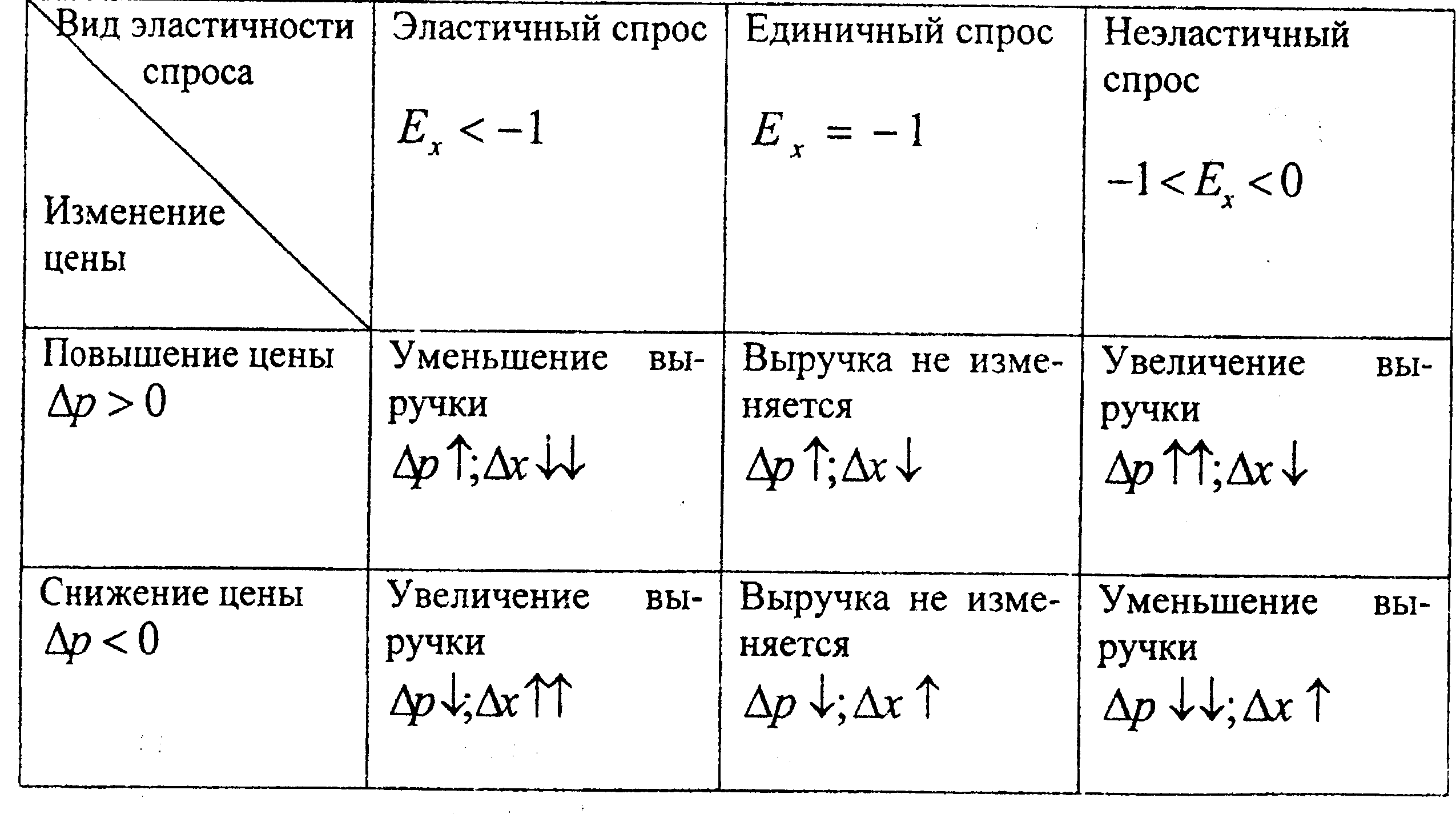

12. Функция непрерывных процентов.

Рассмотрим алгоритм формир-я ф-ции непрер. %. Для этого обозначим через Q сумму вклада по истеч-ии n периодов времени, а через Q₀ – первонач. 𝛴(депозит), помещ. в банк под 100% годовых.Через год 𝛴 депозита составит Q₁ =2Q₀, а через полгода- Пусть последняя 𝛴 вновь будет помещена в кач-ве депозита в том же банке. В этом случае в конце года депозит составит

Если депозит помещать ежеквартально, то , а при ежемесячном размещ-ии в конце года депозит составит Аналогично при ежеднев.: Если операцию открытия-закрытия счета производить непрерывно, то к концу года депозит составит Т. о., при номинальной ставке 100 % и непрерывном на­числении % доход за год может составить не более 172 %. В общем, но реальном, а не идеализированном случае, если % начисления р, а год разбит на п частей, то через tлет 𝛴 депозита достигнет величины Если обозначить через r= p/100, то последнее выр-е можно привести к виду:

Если далее устремить п к бесконечности, то сумма Q₀, вложенная в банк под р %годовых, за tлет достигнет теоретически предель­ной суммы

С оотн-е предст-ет собой ф-wb. непрерыв. %, где в кач-ве аргумента выступает t= 1,2,…n