44.Множественная регрессия. Отбор факторов.
Общее назначение множественной регрессии состоит в анализе связи между несколькими независимыми переменными и зависимой переменной. y = ∑bixi + a
48. Построение балансовой модели
Одним из классов широко используемых экономических моделей, является класс балансовых моделей. Действительно, эффективное ведение корпоративного или государственного, частного или общественного хозяйства предполагает наличие баланса между отдельными отраслями или видами деятельности.
Для описания модели рассмотрим экономическую систему, состоящую из n-отраслей. Каждая из отраслей производит только один вид продукта. Этот продукт частично используется как самой отраслью, так и другими отраслями, но в основном идёт на внепроизводственное потребление.
Обозначим:
– общий объём продукции -й отрасли за определенный отрезок времени, например, за год. Это так называемый валовый продукт -й отрасли;
– объём
продукции
-й
отрасли, расходуемой
-й
отраслью в процессе производства
-го
продукта за тот же отрезок времени;
– объём
продукции
-ой
отрасли, предназначенной для
непроизводственной среды (около 75 %). К
непроизводственной среде относится
личное потребление членов общества,
различного рода запасы, поставки на
экспорт и т. п.
Тогда будет справедливым равенство:
, 
(1.1)
Это
равенство, называемое балансовым,
означает, что продукция, произведенная
-ой
отраслью, расходуется на производственное
потребление
и
непроизводственное
.
Преобразуем равенство (1.1), для чего умножим сумму и разделим на
,
то есть
,
или
.
(1.2)
Обозначим
через
.
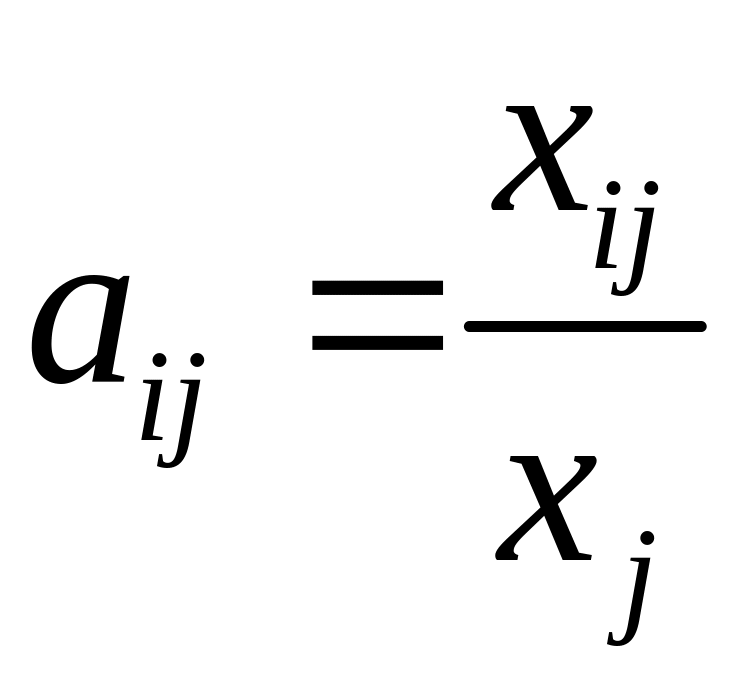Тогда соотношение (1.2) примет вид
,
(1.3)
Здесь
коэффициенты
называются коэффициентами предельных
затрат (коэффициентами материалоемкости).
Другими словами,
есть объем продукции
-й
отрасли, приходящейся на единицу объема
j-й
отрасли, или стоимость продукции
-й
отрасли, вложенной в 1 рубль продукции
j-й
отрасли.
Если ввести вектор-столбцы х, y и матрицу A, то равенство (1.3) можно записать в виде векторно-матричного равенства:
x = Ax + y, (1.4)
где
x
,
y
,
A
,
.
Вектор x в соотношении (1.4) называется вектором валового выпуска (планом), вектор y – вектором конечного потребления, а матрица A – матрицей прямых затрат. Соотношение (1.4) называется уравнением линейного межотраслевого баланса. Вместе с приведённой трактовкой x,y и A соотношение (1.4) называется моделью Леонтьева, или моделью “затраты – выпуск ”.
Из приведённых соотношений следует, что как компоненты векторов x и y, так и элементы матрицы A имеют одну и ту же размерность (кубометры, штуки, тонны, киловатт-часы и т. д.). Такой баланс называют натуральным. В случае когда они выражены в денежных единицах, модель называется стоимостной.
Если
y
,
то есть
(
),
то модель называется замкнутой, в
противном случае – открытой. Для
замкнутой модели характерно, что вся
продукция расходуется внутри экономической
системы.
Уравнение межотраслевого баланса (модель Леонтьева) применяется при планировании вектора валового выпуска. Значения его компонент следуют из решения системы линейных уравнений (1.4) при заданных элементах матрицы A и значении компонент вектора y.