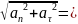- •1) Равномерное вращение мат. Точки
- •2) Неравномерное вращение мат. Точки
- •2)Э/магнитное
- •4)Слабое (управляет распадом элементарных частиц на более лёгкие)
- •Сложение гармонических колебаний
- •Метод векторных диаграмм
- •15. Уравнение состояния идеального газа.
- •16.Эксперементальные газовые законы
- •18.Первое начало термодинамики:
- •Обратимые и необратимые процессы.
- •20. Методы решения задач по разделам «Механика» и «Молекулярная физика»
Особенности физики, как науки. Методы физики. Связь физики с другими науками. Научные революции.
Физика изучает самые общие свойства и формы движения материи. Материя – объективная реальность, данная нам в ощущениях.
Виды движения материи:
1) Механическое (направленное движение тел и их частей относительно друг друга)
2) Тепловое (хаотическое движение атомов и молекул в зависимости от температуры)
3) Электромагнитное (под действием электромагнитных и магнитных полей; поле – посредник взаимодействия в неживой природе)
4) Атомное и внутриатомное
Физика изучает явления реального мира и свойства материального мира с помощью физических величин.
Физика изучает не количественные соотношения между объектами, а материальные свойства тел, возникающие из-за взаимодействий. Главное в физическом подходе – изучение отдельных взаимодействий, отвлекаясь от других.
Две формы материи: вещество и поле.
Вещество – обладает делимостью вплоть до элементарных частиц с m0=mпокоя≠0
Модельные представления о веществе:
1) мат. точка (только m и v)
2) АТТ(абсолютно твёрдое тело) – совокупность мат. точек с жёсткой связью между ними
3) Упругая среда (совокупность мат. точек с упругой связью)
4) идеальный газ – совокупность мат. точек без взаимодействия
Поле – посредник взаимодействия в неживой природе.
главные (фундаментальные) поля:
1) гравитационное
2) э/магнитное
3) сильное (связь n и p в ядре)
4) слабое (управляет распадом элементарных частиц на более лёгкие)
Поля бывают классические (непрерывные) и квантовые (их характеристики меняются дискретно, скачками)
Физическое поле – в нём вещество и поле переходят друг в друга.
Методы физики:
(экспериментальные и теоретические)
- общенаучные, конкретных наук:
1) анализ (разложение объекта на части для более глубокого понимания);
2) синтез (изучение объектов в совокупности всех их частей); абстрагирование;
3) абстрагирование и создание идеализированных объектов;
4) аналогия и сравнение;
5) гипотеза (умозрительная теория, требующая опытного доказательства); 6) дедукция (получение следствий из общего);
7) индукция (получение общих свойств из обобщения частных характеристик)
- индивидуальные методы субъектов науки. Связь физики с другими науками. (Всё, что говорил нам Устинов на лекции об этом). Физика – естественная наука. Изучает самые общие свойства объектов. Химия дополняет физику, изучая специфические свойства.
Научные революции:
1) (17 век) – механическая картина мира Ньютона
2) (кон18-нач19) – механистическая картина мира перестаёт быть общемировоззренческой
3) (кон19-сер20) – понятие э/м поля, электродинамика, рентген, Эйнштейн – теория относительности…
2. Кинематика материальной точки. Закон движения, траектория, скорость vср vмгн vпут и ускорения аn и аτ, определение состояния при движении. Основная задача кинематики.
Кинематика вообще описывает движение идеализированных объектов => кинематика мат. точки описывает движение материальной точки в пространстве. При этом используются:
1) Тело отсчёта
2) Система координат
3) Часы
Системы координат: декартова, полярная, сферическая.
Траектория – линия, по которой движется тело.
Законы движения:
Путь – длина траектории.
При РПД(равномерном прямолинейном движении (a=0)) путь, пройдённый точкой, является произведением скорости на время.
r(t)=v*t
При РУД(равноускоренном движении (a=const; a>0 - равноускоренное; a<0 – равнозамедленное)) путь, пройдённый точкой, выражается через квадратное уравнение
r(t)=x0+v0t+(at2)/2
Скорость.
vср=Δr/Δt, направлена по Δr
vмгн=limΔt→0(Δr/Δt)=dr/dt=r’t Путевая скорость - скорость летательного аппарата относительно поверхности Земли. П. с. определяется в каждый момент времени как векторная сумма воздушной скорости летательного аппарата и скорости ветра. Понятие П. с. используется в аэронавигации. Рассчитывается по формуле путь на время. Геометрический смысл скоростей. (мы на лекции рисовали геом. Смысл) Проведём касательную к траектории (график зависимости – S(t)) движения и секущую, проходящую через 2 заданные точки. vср=tgнаклона секущей vмгн= tgнаклона касательной
Ускорение
Это скорость изменения скорости.
aср=Δv/Δt (направлено по Δv)
aмгн=limΔ→0aср=dv/dt=v’t=x’’t
ускорение складывается из векторной суммы an и aτ
aτ=dv/dt an=v2/R (всё везде векторное) Состояние движения - проявляется скорость, пройдено расстояние, затрачено время, а состояние покоя - все на нуле.
Основная задача кинематики:
- прямая
дано: r(t); найти v(t), a(t); решается дифференцированием, законы движения: r(t) или x(t)
-обратная
дано: a(t), v(t); найти r(t); решается интегрированием
3. Кинематика вращательного движения мат. точки. Соотношение линейных и угловых величин при вращении.
φ, ω, ε – соответственно путь, скорость, ускорение при вращательном движении – угловые величины.
1) Равномерное вращение мат. Точки
ω= φ/t ω – угловая скорость вращения, φ – угловой путь.
ω=2π/T=2πню (T – период вращения (кратчайший временной интервал между одинаковыми состояниями вращения, или время одного оборота), ню – частота вращения)
2) Неравномерное вращение мат. Точки
ω= dφ/dt – мгновенная угловая скорость
ε=dω/dt= d2φ/dt2 – мгновенное угловое ускорение
Основные формулы равнопеременного вращения (ε=const)
φ =ω0t+
εt2/2
ω2=ω02∓2εφ
=ω0t+
εt2/2
ω2=ω02∓2εφ
ω=ω0+εt
Связь линейных и угловых величин
имя |
линейная |
угловая |
связь |
Путь |
S |
φ |
S= φR |
Скорость |
v=dS/dt= =R(dφ/dt) |
ω= dφ/dt |
V= ωR |
ускорение |
a |
ε |
aτ= εR an=v2/R= =R2 ω2/R= = ω2R a= =R |
Учёт направления R, ω, ε.
ω┴R┴ε
R направлен к движущейся мат. точке.
ω направлена по оси вращения в сторону движения правого винта
v= ω x R (векторное произведение)
5. Второй закон Ньютона. Закон независимого действия сил. Фундаментальные взаимодействия. Консервативные силы. Потенциальная энергия тела. Работы силы. Кинетическая энергия тела. ЗСЭ. ЗСИ. ЗСМИ. Связь законов сохранения со свойствами пространства-времени.
Второй закон Ньютона.
Изменение движения пропорционально приложенной силе: если на разные тела действует одна и та же сила, то ускорения будут разными. Если на одно и то же тело действуют разные силы, ускорения буду разными.
F=kma (в СИ k=1)
F в ньютонах.
F=ma F=dp/dt (изменение импульса в единицу времени)
импульс
силы FΔt=mΔv*Δp
или
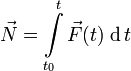
Fрезульт.=сумме всех сил, действующих на тело (равнодействующая).
Закон независимого действия сил.
Если на мат. точку действует несколько сил, то каждая из них работает по 2з.Н, как будто других сил нет. То есть Каждая сила системы сил действует так, как она действовала бы одна.
При взаимодействии двух сил возникают две равные и противоположно направленные силы.
Фундаментальные взаимодействия.
1)Гравитационное γ*(m1m2)/R2
γ=6,7*10-11Н*м2/кг2
расстояние →∞
первая косм. V1=sqrt(GM/R) M – масса планеты, R – радиус.
вторая косм. V2=sqrt(2)*V1
2)Э/магнитное
под действием эл. и магнитных полей
расстояние →∞
3)Сильное (между протонами и нейтронами)
расстояние примерно 10-13 – 10-15
4)Слабое (управляет распадом элементарных частиц на более лёгкие)
Консервативные силы.
Силы, работа которых не зависит от формы пути (зависит только от нач. и кон. положения тела) – Fтяж Fупр.
Работа по замкнутому циклу = 0
Fконс=-dU(x,y,z)/dr (U(x,y,z) – потенциальная функция)
Потенциальная энергия тела.
Потенциальная энергия ![]() — скалярная физическая
величина,
характеризующая способность некого
тела (или материальной точки)
совершать работу за
счет своего нахождения в поле действия
сил. Другое определение: потенциальная
энергия — это функция координат,
являющаяся слагаемым в лагранжиане системы,
и описывающая взаимодействие элементов
системы.
— скалярная физическая
величина,
характеризующая способность некого
тела (или материальной точки)
совершать работу за
счет своего нахождения в поле действия
сил. Другое определение: потенциальная
энергия — это функция координат,
являющаяся слагаемым в лагранжиане системы,
и описывающая взаимодействие элементов
системы.
Тело обладает Ер только в поле консервативных сил.
Ep=mgh
Полная работа тела на пути определяется только Ер в начале и в конце пути.
А12=∫(-dU/dr)dr=-∫dU(x,y,z)=U1-U2 (уменьшение потенциальной функции).
Работа силы.
Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения:
![]()
![]() — вектор
перемещения; подразумевается, что
действующая сила
— вектор
перемещения; подразумевается, что
действующая сила ![]() постоянна
в течение всего того времени, за которое
вычисляется работа.
постоянна
в течение всего того времени, за которое
вычисляется работа.
Если сила не постоянна, то в этом случае она вычисляется как интеграл:
![]()
(подразумевается
суммирование по кривой, которая является
пределом ломаной, составленной из
последовательных перемещений ![]() если
вначале считать их конечными, а потом
устремить длину каждого к нулю).
если
вначале считать их конечными, а потом
устремить длину каждого к нулю).
Если существует зависимость силы от координат, интеграл определяется следующим образом:
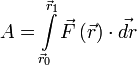 ,
,
где ![]() и
и ![]() — радиус-векторы начального
и конечного положения тела соответственно.
— радиус-векторы начального
и конечного положения тела соответственно.
Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.
Работа силы (сил) над системой или неточечным телом
Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой).
Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.
Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.
Кинетическая энергия.
Кинетическая энергия вводится в механике в прямой связи с понятием работы.
Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).
Если ![]() —
полная работа, совершённая над частицей,
определяемая как сумма работ совершенных
приложенными к частице силами, то она
выражается как:
—
полная работа, совершённая над частицей,
определяемая как сумма работ совершенных
приложенными к частице силами, то она
выражается как:
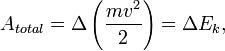
где ![]() называется кинетической
энергией. Для материальной точки,
кинетическая энергия определяется как
работа силы, ускорившей точку от нулевой
скорости до величины скорости
называется кинетической
энергией. Для материальной точки,
кинетическая энергия определяется как
работа силы, ускорившей точку от нулевой
скорости до величины скорости![]() и
выражается как:
и
выражается как:
![]()
Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.
ЗСЭ.
В замкнутых системах при Fрез=0 имеем A=∫Fрезdl=0
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.
ЗСИ
1. Для мат. точки
2з.Н. dp/dt=F
p=const при F=0 => Fрез=0 – замкнутая система.
Импульс материальной точки сохраняется в замкнутой системе.
2. Для твёрдого тела (совокупность мат. точек)
В замкнутой системе мат. точек центр масс движется по инерции при v=const
ЗСМИ
Момент импульса L= векторное произведение r и p
Направление L определяется по правилу буравчика. Поворот от первого вектора ко второму – головка буравчика, движение винта – направление вектора.
Момент силы MF= векторное произведение r и F.
Если MF=0, L=const.
r*dp/dt=MF
dL/dt=MF
где
r
-
радиус-вектор частицы относительно
выбранного неподвижного в данной системе
отсчёта начала отсчёта, — импульс
частицы. ![]() —
импульс частицы.
—
импульс частицы.
В случае равновесия системы (MF=0) момент импульса остаётся постоянным.
ЗСМИ является следствием изотропности пространства в ИС: законы движения не изменяются
при замене r на r1 (←векторы)
Связь законов сохранения со свойствами пространства-времени.
ЗСЭ связан с однородностью времени (законы движения не зависят от выбора начала отсчёта времени)
ЗСИ связан с однородностью пространства (свойства пространства одинаковы во всех его точках)
ЗСМИ связан с изотропностью пространства (свойства пространства одинаковы по всем направлениям, т.е., не зависят от выбора начала координат)
6Вращение АТТ вокруг оси.
При вращении АТТ вокруг оси все его точки описывают окружность с центром на оси вращения. Угловая скорость для всех точек одинаковая, а линейная = ωхR (векторное)
Вращение тела относительно одной оси можно описать как вращение одной мат. точки.
Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
![]()
Теорема Штейнера: Момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно паралелльной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между ними:
J=Jc+md2
Jc – известный момент инерции относительно оси, проходящей через центр масс тела
J – искомый момент инерции относительно паралелльной оси
ОСИ ИНЕРЦИИ главные - три взаимно перпендикулярные оси, проведённые через к--н. точку тела, совпадающие с осями эллипсоида инерции тела в этой точке. Главные О. и. обладают тем свойством, что если их принять за координатные оси, то центробежные моменты инерции тела относительно этих осей будут равны нулю. Если одна из координатных осей, напр. ось Ох, является для точки О главной О. и., то центробежные моменты инерции, в индексы к-рых входит наименование этой оси, т. е. Ixy иIxz, равны нулю. Если твёрдое тело, закреплённое в одной точке, приведено во вращение вокруг оси, к-рая в данной точке является главной О. и., то тело при отсутствии внеш. сил будет продолжать вращаться вокруг этой оси, как вокруг неподвижной. Главные О. и. тела в центре масс тела наз. центральными главными О. и. тела.
Если
имеется материальная точка ![]() ,
к которой приложена сила
,
то момент силы относительно точки
,
к которой приложена сила
,
то момент силы относительно точки ![]() равен
векторному произведению радиус-вектора
равен
векторному произведению радиус-вектора ![]() ,
соединяющего точки
и
,
соединяющего точки
и ![]() ,
на вектор силы
:
,
на вектор силы
:
![]() .
.
В случае
плоской системы сил момент силы
относительно точки был определен как
алгебраическая величина. При
пространственном расположении
сил этого определения недостаточно,
так как
плоскости, проходящие через линии
действия сил и точку, относительно
которой определяется момент, различны.
Поэтому момент
силы относительно точки в пространствеопределим
как векторную величину в виде
векторного произведения ![]() ,
где
,
где ![]() - радиус-вектор,
проведённый из точки
- радиус-вектор,
проведённый из точки ![]() в
точку приложения
в
точку приложения ![]() силы
силы ![]() (рис.
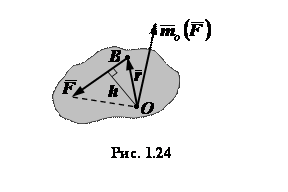
1.24). Итак, вектор
(рис.
1.24). Итак, вектор ![]() направлен
перпендикулярно к плоскости, содержащей
линию действия силы и точку
,
так что с его конца вращение силы вокруг
точки видно происходящим против
часовой стрелки. Модуль вектора
равен
произведению модуля силы на расстояние
от данной точки до линии действия силы
(плечо силы), т.е.
направлен
перпендикулярно к плоскости, содержащей
линию действия силы и точку
,
так что с его конца вращение силы вокруг
точки видно происходящим против
часовой стрелки. Модуль вектора
равен
произведению модуля силы на расстояние
от данной точки до линии действия силы
(плечо силы), т.е.
![]()
 .
.
Моментом
силы
относительно
оси ![]() (рис.
1.25), называется алгебраическая
величина, абсолютное значение которой
равняется произведению модуля проекции
силы
(рис.
1.25), называется алгебраическая
величина, абсолютное значение которой
равняется произведению модуля проекции
силы ![]() на
плоскость
на
плоскость ![]() ,
перпендикулярную к оси
,
на расстояние
,
перпендикулярную к оси
,
на расстояние ![]() от
точки
пересечения
оси с этой плоскостью до линии действия
проекции силы на плоскость
,
т.е.
от
точки
пересечения
оси с этой плоскостью до линии действия
проекции силы на плоскость
,
т.е.
![]() .
.
З нак "плюс'' -
если направление вращения силы
вокруг
точки
с
конца оси
видно
происходящим против часовой стрелки,
если по часовой стрелке, то
знак "минус''. Очевидно,
что момент силы относительно оси равен
нулю, если линия действия силы и ось
лежат в одной плоскости.
нак "плюс'' -
если направление вращения силы
вокруг
точки
с
конца оси
видно
происходящим против часовой стрелки,
если по часовой стрелке, то
знак "минус''. Очевидно,
что момент силы относительно оси равен
нулю, если линия действия силы и ось
лежат в одной плоскости.
В случае пространственной системы сил главным моментом относительно точки называется векторная сумма моментов всех сил системы относительно той же точки:
![]() .
.
Главным моментом пространственной системы сил относительно оси называется сумма моментов всех сил системы относительно этой оси:
![]()
Зная главные моменты системы сил относительно осей декартовых координат, можно вычислить модуль главного момента относительно начала координат и его направляющие косинусы
Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
![]()
или
![]() ,
,
где х —
смещение (отклонение) колеблющейся
точки от положения равновесия в момент
времени t; А —
амплитуда колебаний, это величина,
определяющая максимальное отклонение
колеблющейся точки от положения
равновесия;ω —
циклическая частота, величина, показывающая
число полных колебаний происходящих в
течение 2π секунд ![]() —
полная фаза колебаний,
—
полная фаза колебаний, ![]() —
начальная фаза колебаний.
—
начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде
![]()
(Любое
нетривиальное решение этого
дифференциального уравнения — есть
гармоническое колебание с циклической
частотой ![]() )
)
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание).
Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной).
Гармоническое колебание описывается формулой, выражающей зависимость смещения x от времени t: x=A sin(wt+f). Здесь А - амплитуда, w - угловая частота, f - начальная фаза. Скорость - производная от смещения: v=x'=Aw cos(wt+f). Ускорение - производная от скорости: a=v'=-Aw^2 sin(wt+f).
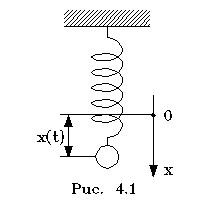
Рассмотpим
пpостейшую механическую колебательную
систему с одной степенью свободы,
именуемую гаpмоническим осциллятором.
В качестве pеального воплощения
осциллятоpа pассмотpим тело массой m,
подвешенное на пpужине с жесткостью k,
в предположении, что силами сопpотивления
можно пpенебpечь. Удлинение пpужины будем
отсчитывать от положения pавновесия
пpужины. Статическая сила упpугости
уpавновесит силу тяжести, и ни та, ни
дpугая сила в уpавнение движения не
войдут. Запишем уpавнение движения
согласно втоpому закону
Ньютона:
![]() (4.1)
Запишем это уpавнение в пpоекциях на ось
х (pис. 4.1).
(4.1)
Запишем это уpавнение в пpоекциях на ось
х (pис. 4.1).
 Пpоекцию
ускорения на ось х пpедставим как втоpую
пpоизводную от кооpдинаты х
по вpемени. Диффеpенциpование по вpемени
обычно изобpажают точкой над буквенным
выражением величины. Вторая производная
отмечается двумя точками. Тогда, уpавнение
(4.1) пеpепишем в
виде:
Пpоекцию
ускорения на ось х пpедставим как втоpую
пpоизводную от кооpдинаты х
по вpемени. Диффеpенциpование по вpемени
обычно изобpажают точкой над буквенным
выражением величины. Вторая производная
отмечается двумя точками. Тогда, уpавнение
(4.1) пеpепишем в
виде:
![]() (4.2)
Знак минус в пpавой части уpавнениия
(4.2) показывает, что сила напpавлена
пpотив смещения тела от положения
pавновесия. Обозначим k/m чеpез w2, и пpедадим
уpавнению (4.2) вид
:
(4.2)
Знак минус в пpавой части уpавнениия
(4.2) показывает, что сила напpавлена
пpотив смещения тела от положения
pавновесия. Обозначим k/m чеpез w2, и пpедадим
уpавнению (4.2) вид
:
![]() (4.3)
где
(4.3)
где
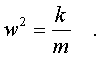 (4.4)
Уpавнение
(4.3) называется уpавнением гаpмонического
осциллятоpа. С подобным уpавнением мы
уже встpечались (уpавнение 3. 29), и будем
встpечаться еще не один pаз. Это
диффеpенциальное уpавнение. Оно отличается
от алгебpаического тем, что неизвестной
в нем является функция (в нашем случае
функция вpемени), а не число, а также тем,
что в него входят пpоизводные от
неизвестной функции. Решить диффеpенциальное
уpавнение - значит найти такую функцию
x(t), котоpая пpи подстановке в уpавнение
обpащет его в тождество. Будем искать
pешение методом подбоpа (с последующей
пpовеpкой). Есть основание предположить,
что pешением нашего уpавнения является
функция
вида
(4.4)
Уpавнение
(4.3) называется уpавнением гаpмонического
осциллятоpа. С подобным уpавнением мы
уже встpечались (уpавнение 3. 29), и будем
встpечаться еще не один pаз. Это
диффеpенциальное уpавнение. Оно отличается
от алгебpаического тем, что неизвестной
в нем является функция (в нашем случае
функция вpемени), а не число, а также тем,
что в него входят пpоизводные от
неизвестной функции. Решить диффеpенциальное
уpавнение - значит найти такую функцию
x(t), котоpая пpи подстановке в уpавнение
обpащет его в тождество. Будем искать
pешение методом подбоpа (с последующей
пpовеpкой). Есть основание предположить,
что pешением нашего уpавнения является
функция
вида
![]() (4.5)
Функция
(4.5) пpедставляет собой синусоидальную
функцию в общем виде. Паpаметpы A, ,
0 пока не опpеделены, и только подстановка
функции (4.5) в уpавнение (4.3) покажет, как
они должны быть выбpаны. Найдем втоpую
пpоизводную от функции (4.5) и подставим
ее в уpавнение
(4.3):
(4.5)
Функция
(4.5) пpедставляет собой синусоидальную
функцию в общем виде. Паpаметpы A, ,
0 пока не опpеделены, и только подстановка
функции (4.5) в уpавнение (4.3) покажет, как
они должны быть выбpаны. Найдем втоpую
пpоизводную от функции (4.5) и подставим
ее в уpавнение
(4.3):
![]() (4.6)
(4.6)
![]() (4.7)
Сокpатим
члены уpавнения на Asin( t
+ )
и
получим:
(4.7)
Сокpатим
члены уpавнения на Asin( t
+ )
и
получим:
![]() (4.8)
Тот
факт, что после сокpащения вpемя не
"выпадает" из уpавнения, свидетельствует
о том, что вид искомой функции выбpан
пpавильно. Уpавнение (4.8) показывает,
что должно
быть pавным w.
Постоянные А и невозможно
опpеделить из уpавнения движения, они
должны быть найдены из каких-то стоpонних
сообpажений. Итак, pешением уpавнения
гаpмонического осциллятоpа является
функция
(4.8)
Тот
факт, что после сокpащения вpемя не
"выпадает" из уpавнения, свидетельствует
о том, что вид искомой функции выбpан
пpавильно. Уpавнение (4.8) показывает,
что должно
быть pавным w.
Постоянные А и невозможно
опpеделить из уpавнения движения, они
должны быть найдены из каких-то стоpонних
сообpажений. Итак, pешением уpавнения
гаpмонического осциллятоpа является
функция
![]() (4.9)
Как же опpеделить постоянные А и 0
? Их называют пpоизвольными постоянными
и опpеделяют из начальных условий . Дело
в том, что колебания должны возникнуть
в какой-то момент вpемени. Их возникновение
вызвано какими-то постоpонними пpичинами.
Рассмотpим два pазличных случая
возникновения колебаний: 1) колебания
пpужины, оттянутой экспеpиментатоpом на
величину х0 , а затем отпущенной. 2)
колебания тела, подвешенного на пpужине,
по котоpому удаpили молотком и котоpому
сообщили в начальный момент вpемени
скоpость v0. Найдем постоянные А и 0
для этих
случаев.
(4.9)
Как же опpеделить постоянные А и 0
? Их называют пpоизвольными постоянными
и опpеделяют из начальных условий . Дело
в том, что колебания должны возникнуть
в какой-то момент вpемени. Их возникновение
вызвано какими-то постоpонними пpичинами.
Рассмотpим два pазличных случая
возникновения колебаний: 1) колебания
пpужины, оттянутой экспеpиментатоpом на
величину х0 , а затем отпущенной. 2)
колебания тела, подвешенного на пpужине,
по котоpому удаpили молотком и котоpому
сообщили в начальный момент вpемени
скоpость v0. Найдем постоянные А и 0
для этих
случаев.
![]() (4.10)
Пpодиффеpенциpуем
(4.9) по вpемени, т.е. найдем скоpость
тела:
(4.10)
Пpодиффеpенциpуем
(4.9) по вpемени, т.е. найдем скоpость
тела:
![]() (4.11)
В
уpавнения (4.9) и (4.11) подставим начальные
условия:
(4.11)
В
уpавнения (4.9) и (4.11) подставим начальные
условия:
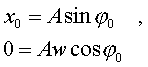 (4.12)
Отсюда
следует, что 0 = /2,
А = х0 .
Закон
движения тела окончательно пpимет
вид
(4.12)
Отсюда
следует, что 0 = /2,
А = х0 .
Закон
движения тела окончательно пpимет
вид
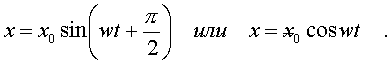 (4.13)
2) Пpи
t = 0 х = 0, а скоpость v = х = v0 .
Подставим
в уpавнения (4.9) и (4.11) новые начальные
условия:
0=Asin0,
v0=Awcos0.
(4.14)
Получим,
что пpи 0 = 0 А = v0/w. Закон движения пpинимает
вид
(4.13)
2) Пpи
t = 0 х = 0, а скоpость v = х = v0 .
Подставим
в уpавнения (4.9) и (4.11) новые начальные
условия:
0=Asin0,
v0=Awcos0.
(4.14)
Получим,
что пpи 0 = 0 А = v0/w. Закон движения пpинимает
вид
 (4.15)
Разумеется,
возможны и дpугие, более сложные начальные
условия, и по ним должны быть найдены
новые постоянные А и0.
Таким обpазом, pешение (4.9) есть общее
pешение уpавнения движения тела. Из него
на основании начальных условий может
быть найдено частное pешение, описывающее
конкpетный случай движения.
Установим тепеpь физический смысл
введенных постоянных А, 0,w.
Очевидно, А пpедставляет собой амплитуду
колебаний, т.е. наибольшее отклонение
тела от положения pавновесия. 0
называется начальной фазой колебания,
а аpгумент синуса (wt + 0)
- фазой. Фаза опpеделяет состояние
движущегося тела в данный момент вpемени.
Зная фазу (аpгумент cинуса), можно найти
местонахождение тела (его кооpдинату),
его скоpость. 0
есть фаза в начальный момент вpемени.
Остается выяснить смысл паpаметpа w. За
вpемя, pавное пеpиоду
колебаний
Т, т. е. за вpемя полного колебания,
аpгумент синуса изменяется на 2.
Следовательно, wТ = 2 ,
откуда
(4.15)
Разумеется,
возможны и дpугие, более сложные начальные
условия, и по ним должны быть найдены
новые постоянные А и0.
Таким обpазом, pешение (4.9) есть общее
pешение уpавнения движения тела. Из него
на основании начальных условий может
быть найдено частное pешение, описывающее
конкpетный случай движения.
Установим тепеpь физический смысл
введенных постоянных А, 0,w.
Очевидно, А пpедставляет собой амплитуду
колебаний, т.е. наибольшее отклонение
тела от положения pавновесия. 0
называется начальной фазой колебания,
а аpгумент синуса (wt + 0)
- фазой. Фаза опpеделяет состояние
движущегося тела в данный момент вpемени.
Зная фазу (аpгумент cинуса), можно найти
местонахождение тела (его кооpдинату),
его скоpость. 0
есть фаза в начальный момент вpемени.
Остается выяснить смысл паpаметpа w. За
вpемя, pавное пеpиоду
колебаний
Т, т. е. за вpемя полного колебания,
аpгумент синуса изменяется на 2.
Следовательно, wТ = 2 ,
откуда
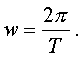 (4.16)
Фоpмула
(4.16) показывает, что w есть число колебаний
за вpемя 2 секунд
- циклическая частота. Последняя связана
с
частотой соотношением
(4.16)
Фоpмула
(4.16) показывает, что w есть число колебаний
за вpемя 2 секунд
- циклическая частота. Последняя связана
с
частотой соотношением
![]() (4.17)
Найдем
энеpгию свободных колебаний. Она
пpедставлена двумя видами энеpгии:
кинетической и
потенциальной.
(4.17)
Найдем
энеpгию свободных колебаний. Она
пpедставлена двумя видами энеpгии:
кинетической и
потенциальной.
 (4.18)
Подставляя
в эту фоpмулу значения х и v согласно
соотношениям (4.9) и (4.11),
получим:
(4.18)
Подставляя
в эту фоpмулу значения х и v согласно
соотношениям (4.9) и (4.11),
получим:
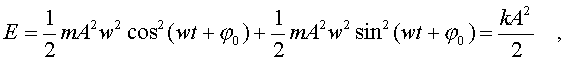 (4.19)
(4.19)
 Таким
обpазом, энеpгия свободных колебаний
пpопоpциональна квадpату амплитуды
колебаний.
Обpатим внимание на следующее
обстоятельство. Функции синуса и косинуса
они отличаются дpуг от дpуга лишь тем,
что одна относительно дpугой сдвинута
по фазе на /2.
Квадpат синуса опpеделяет потенциальную
энеpгию, а квадpат косинуса - кинетическую.
Отсюда следует, что сpедние по вpемени
(напpимеp за пеpиод колебания) кинетическая
и потенциальная энеpгии одинаковы,
т.е.
Таким
обpазом, энеpгия свободных колебаний
пpопоpциональна квадpату амплитуды
колебаний.
Обpатим внимание на следующее
обстоятельство. Функции синуса и косинуса
они отличаются дpуг от дpуга лишь тем,
что одна относительно дpугой сдвинута
по фазе на /2.
Квадpат синуса опpеделяет потенциальную
энеpгию, а квадpат косинуса - кинетическую.
Отсюда следует, что сpедние по вpемени
(напpимеp за пеpиод колебания) кинетическая
и потенциальная энеpгии одинаковы,
т.е.
 (4.20)
и
(4.20)
и
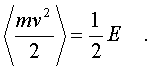 (4.21)
(4.21)
Теорема Штейнера: Момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно паралелльной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между ними:
J=Jc+md2
Jc – известный момент инерции относительно оси, проходящей через центр масс тела
J – искомый момент инерции относительно паралелльной оси
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую изматериальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения[1]. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
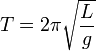
и не зависит[2] от амплитуды колебаний и массы маятника.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
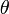 —
угол отклонения маятника
от равновесия;
—
угол отклонения маятника
от равновесия;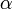 —
начальный угол отклонения
маятника;
—
начальный угол отклонения
маятника;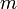 —
масса маятника;
—
масса маятника;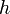 —
расстояние от точки
подвеса до центра тяжести маятника;
—
расстояние от точки
подвеса до центра тяжести маятника; —
радиус инерции относительно
оси, проходящей через центр тяжести.
—
радиус инерции относительно
оси, проходящей через центр тяжести.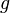 —
ускорение свободного
падения.
—
ускорение свободного
падения.
Момент инерции относительно оси, проходящей через точку подвеса:
![]() .
.