3.2. Алгоритм криптографической системы на основе вычисления дискретных логарифмов в конечном поле – алгоритм Эль Гамаля.

Указанная схема алгоритма криптографических преобразований была предложена Тахиром Эль Гамалем в 1985 году (США), она обусловлена сложностью вычисления дискретных логарифмов в конечном поле. Последовательность действий аналогична алгоритму факторизации больших чисел RSA.

Действия абонента В – абонента получателя закриптгорафированного (зашифрованного) сообщения.

1. На первом шаге алгоритма абонент В формирует (генерирует) пару ключей шифрования-дешифрования передаваемых сообщений: К_ОВ - открытый ключ, предназначенный для шифрования открытых сообщений; К_ЗВ – закрытый (секретный) ключ, предназначенный для дешифрования принимаемых криптограмм.

Изначально, со стороны абонента В (абонента – получателя зашифрованных сообщений) случайным образом задается большое простое число Р (модуль производимых вычислений). На практике это число составляет более 100 десятичных знаков, для упрощения процесса изучения алгоритма Эль Гамаля принимается число Р = 977, затем выбирается целое число G < Р, примем G = 378.

2. На втором шаге алгоритмизации случайным образом задается целое число К_ЗВ –закрытый (секретный) ключ для дешифрования принимаемых закриптографированных сообщений, для примера принимается К_ЗВ = 529; условием ограничения является К_ЗВ < Р.

3. Вычисляется значение открытого ключа абонента В, предназначенного для шифрования открытых сообщений для абонента В:

К_ОВ = mod P = 378⁵²⁹ mod 977 = 402 mod 977 → 402.

4. Числовые значения P, G, К_ОВ являются открытыми параметрами криптографической системы и передаются по незащищенному каналу всем абонентам связи, в частности и абоненту А для обеспечения возможности абоненту-отправителю использовать эти параметры для шифрования открытых сообщений для абонента В. Параметры P и G многопользовательской корпоративной системы защиты и аутентификации электронных сообщений распространяются между всеми абонентами передачи-приема зашифрованных сообщений и являются постоянными для определенного временного интервала, задаваемого администратором безопасности.

Параметры К_ОВ –открытый ключ и К_ЗВ-закрытый (секретный) ключ формируются индивидуально на каждом рабочем месте абонента защищенной связи. К_ЗВ-закрытый (секретный) ключ хранится у каждого абонента в защищенном варианте (на съемных носителях) и никогда никому не передается. Открытыми ключами К_О все абоненты телекоммуникационной системы обмениваются между собой по открытым каналам.

В рассматриваемом примере параметры P, G, K_OB от абонента В передаются открыто абоненту А.

Действия абонента А для формирования криптограмм открытых сообщений для абонента В.

1. Абонент А свое открытое сообщение, предназначенное для шифрования и передачи сформированной криптограммы абоненту-получателю В, отображает в виде целых чисел в соответствии с принятой таблицей (например, таблица Windows-кодировки). Рассмотрим пример составления криптограммы слова «Криптон». К → 171; р → 209; и → 201; п → 208; т→211; о → 207; н → 206.

2. Для того, чтобы зашифровать сообщение М→ «Криптон» абонент А выбирает случайным образом целое число «К» с учетом следующих условий 1 < К < Р-1; НОД (К; (Р-1)) = 1. Условие, что наибольший общий делитель (НОД) чисел К и (Р-1) равен единице, означает их взаимную простоту. Т.е. число К должно быть взаимопростым с числом (Р-1) = 976 и лежать в пределах от 1 до 976. Например принимается К=473. Необходимо отметить, что для каждого сеанса обмена зашифрованными сообщениями число К индивидуально.

3. Абонент А производит вычисление чисел для формирования криптограммы для абонента В. Изначально вычисляется общее для данной криптограммы число a = G^K mod P. Для рассматриваемого примера К=473; G=378; Р=977 следовательно число a = 378⁴⁷³ mod 977 = 950 mod 977 → U. Затем вычисляются криптографические значения каждого символа открытого текста в соответствии со следующей зависимостью:

C_i = (K_OB)^K * M_i mod P.

Для рассматриваемого примера: C_i = 402⁴⁷³ * M_i mod 977.

С₁ = 402⁴⁷³ * M₁ mod P = 402⁴⁷³ * 171 mod 977 = 497 mod 977 → 497 → P;

С₂ = 402⁴⁷³ * M₂ mod P = 402⁴⁷³ * 209 mod 977 = 716 mod 977 → 716 → K;

С₃ = 402⁴⁷³ * M₃ mod P = 402⁴⁷³ * 201 mod 977 = 927 mod 977 → 927 → >;

С₄ = 402⁴⁷³ * M₄ mod P = 402⁴⁷³ * 208 mod 977 = 376 mod 977 → 376 → . ;

С₅ = 402⁴⁷³ * M₅ mod P = 402⁴⁷³ * 211 mod 977 = 419 mod 977 → 419 → B ;

С₆ = 402⁴⁷³ * M₆ mod P = 402⁴⁷³ * 207 mod 977 = 36 mod 977 → 36 → C;

С₇ = 402⁴⁷³ * M₇ mod P = 402⁴⁷³ * 206 mod 977 = 673 mod 977 → 673 → L;

Два числа (a; C_i) для каждого семантического символа открытого сообщения являются его криптограммой. Общий вид криптограммы всего открытого сообщения «Криптон» имеет следующее отображение:

С = {950 497; 950 716; 950 927; 950 376; 950 419; 950 36; 950 673} →

→ {U P; U K; U >; U .; U b; U C; U L}.

Как видно из отображения криптограммы «С» в случае ее формирования по алгоритму Эль Гамаля (алгоритм дискретного логарифмирования в конечном поле) длина шифртекста становится вдвое больше длины исходного открытого сообщения «М». Таким образом, со стороны абонента А формируется криптограмма С для абонента В с помощью открытого ключа абонента В – К_ОВ. Эта криптограмма по каналам теледоступа передается от абонента А к абоненту В. Получив криптограмму С, абонент В производит ее дешифрование с помощью своего секретного ключа К_ЗВ, который хранится только у абонента В под секретом.

Действие абонента В по приему и расшифровки криптограммы С, полученной от абонента А.

4. Абонент В по сетевым каналам телекоммуникаций принимает криптограмму С от абонента-отправителя А, которая зашифрована открытым ключом абонента В – К_ОВ. В этом случае абонент В является санкционированным абонентом, имеющим специальный закрытый (секретный) ключ – К_ЗВ непосредственно функционально связанный с открытым ключом К_ОВ, с помощью которого и была сформирована криптограмма С.

С помощью своего закрытого (секретного) ключа К_ЗВ абонент В производит дешифрование криптограммы, полученной от абонента А, используя следующие функциональные преобразования:

M_i = mod P

Каждый элемент криптограммы дешифруется самостоятельно, в рассматриваемом примере а = 950; К_ЗВ = 529; Р = 977.

M_i = mod 977

Выполнив операцию возведения числа в степень по модулю знаменателя представленной зависимости, получают:

950⁵²⁹ mod 977 = 340 mod 977 → 340.

Методика такого вычисления приведена в разделе 2.3, а сам алгоритм представлен на рис. 3.

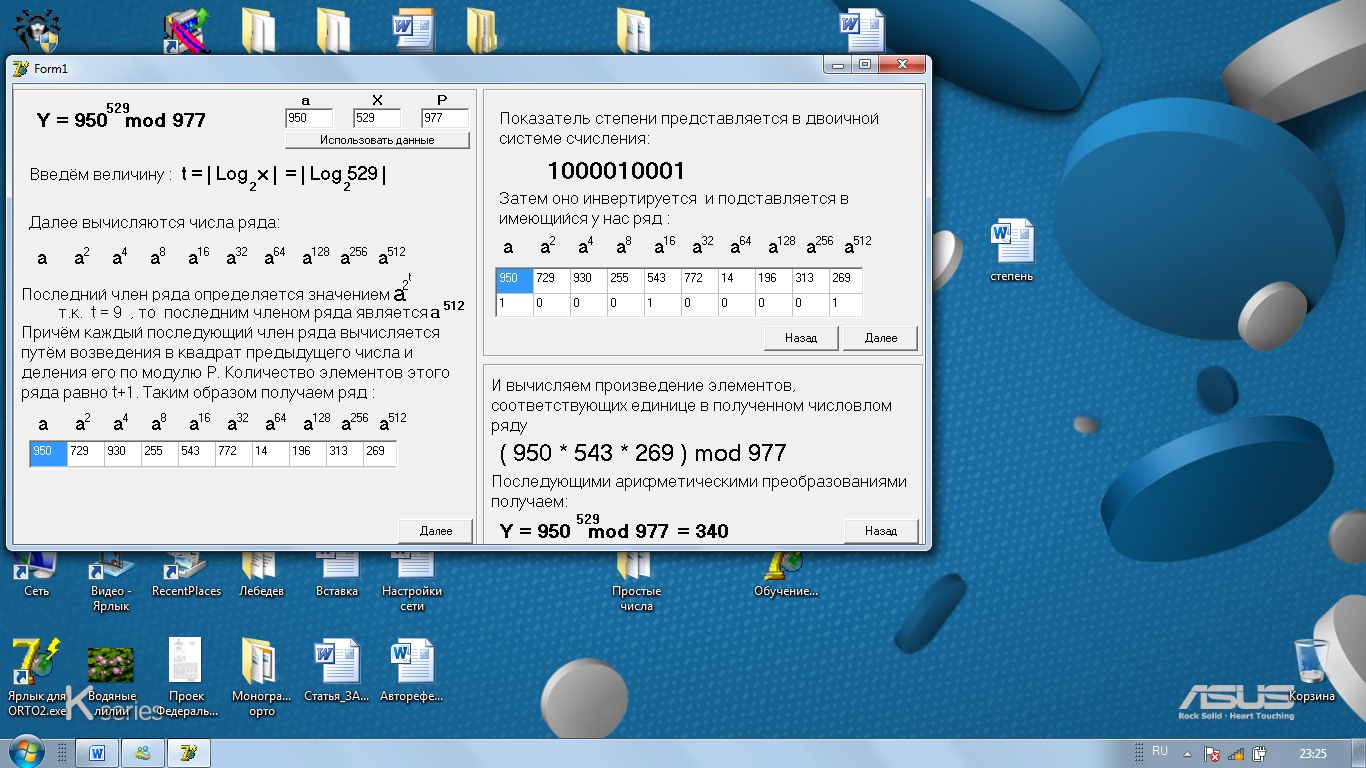
Рис.3. Алгоритм возведения числа а = 950 в степень 529 по модулю 977.

После выполнения операции возведения числа «а = 950» в степень 529 по модулю 977 получают соответствие функционального преобразования криптограммы в открытый текст сообщения, принятого от абонента А.

M_i = mod 977

Для вычисления значений открытого текста необходимо воспользоваться методом вычисления обратных величин по модулю. Для чего значение M_i представляется как: M_i = C_i * 340^-1 mod 977.

Изначально вычисляется значение инверсии числа 340 по модулю 977, т.к. число 977 является простым числом, то это преобразование может быть отображено как: 340^-1 mod 977 = 340^φ(P)-1 mod P, т.к. Р – простое число, то φ(Р) = Р-1 = 977 – 1 = 976.

Следовательно, 340^-1 mod 977 = 340⁹⁷⁵ mod 977 = 250 mod 977

Для вычисления значений M_i получаем следующую зависимость:

M_i = C_i * 250 mod 977

Откуда получаем:

M₁ = C₁ * 250 mod 977 = 497 * 250 mod 977 = 124250 mod977 = 171 mod977

→ К;

M₂ = C₂ * 250 mod 977 = 716 * 250 mod 977 = 179000 mod977 = 209 mod977

→ р;

M₃ = C₃ * 250 mod 977 = 927 * 250 mod 977 = 231750 mod977 = 201 mod977

→ и;

M₄ = C₄ * 250 mod 977 = 376 * 250 mod 977 = 94000 mod977 = 208 mod977

→ п;

M₅ = C₅ * 250 mod 977 = 419 * 250 mod 977 = 104750 mod977 = 211 mod977

→ т;

M₆ = C₆ * 250 mod 977 = 36 * 250 mod 977 = 9000 mod977 = 207 mod977

→ о;

M₇ = C₇ * 250 mod 977 = 673 * 250 mod 977 = 168250 mod977 = 206 mod977

→ н.

Таким образом, при дешифровании с помощью закрытого (секретного) ключа абонента В произведено восстановление принятого закриптографированного сообщения.