2.3. Алгоритм операции возведения числа в степень по модулю.

Этот алгоритм является одной из важнейших операций в криптографических преобразованиях с открытым ключом. Для простоты рассуждений рассмотрим этот алгоритм на численном примере.

Например, требуется вычислить y = a^x mod P при числовом отображении y = 6¹⁸¹ mod 77.

Во всех вычислениях степенной функции по модулю на первом шаге вводится параметр t =  log ₂ X  – целая часть log ₂ X. Символы … означают, выбор целой части включенного выражения.

Если y = a^x mod P, где: а = 6; х = 181; Р = 77, то y = 6¹⁸¹ mod 77.

1. На первом шаге алгоритма определяется значение целой части логарифма по модулю 2 показателя степени х ( в примере х = 181) t =  log ₂ 181;

2^t ≤ х = 2^t ≤ 181, откуда t = 7, следовательно, 2⁷ ≤ 181; 128 ≤ 181.

2. На втором шаге алгоритма вычисляются числа ряда S_i = aⁿ, где n = 2^t . В рассматриваемом числовом примере t = 7, следовательно, последний член ряда определится как S₇ = a¹²⁸. Таким образом, искомый числовой ряд может быть представлен следующим образом:

S_i → а а² а⁴ а⁸ а¹⁶ а³² а⁶⁴ а¹²⁸, т.к. а = 6; Р = 77, то степенные значения ряда вычисляются по модулю Р = 77

а а² а⁴ а⁸ а¹⁶ а³² а⁶⁴ а¹²⁸

6 36 64 15 71 36 64 15 при а =6 по mod Р (Р = 77)

1. После вычисления значений степенного ряда необходимо показатель степени выражения y = a^x mod P отобразить в двоичной форме

Х = 181 → (1 0 1 1 0 1 0 1)₂ ; 1 0 1 1 0 1 0 1 → 2⁷+2⁵+2⁴+2²+2⁰ = 128+32+16+4+1 = 181.

4. Составляется следующая таблица

а128	а64	а32	а16	а8	а4	а2	а0	Искомый ряд
1	0	1	1	0	1	0	1	Двоичное представление показателя степени «Х»
15	64	36	71	15	64	36	6	Численные значения ряда Si

В соответствии со значением отображения показателя степени «х» в двоичной форме вычисляется произведение:

П = (а¹²⁸ * а³² * а¹⁶ * а⁴ * а⁰) mod P = (15 * 36 * 71 * 64 * 6) mod 77 =

= (14722560) mod 77 = 6 mod 77 ≡ 6.

Следовательно, 6¹⁸¹mod 77 = 6 mod 77 ≡ 6.

На рис.2 представлен фрагмент вычисления степенной функции по модули в рамках разработанной автором автоматизированной обучающей системы.

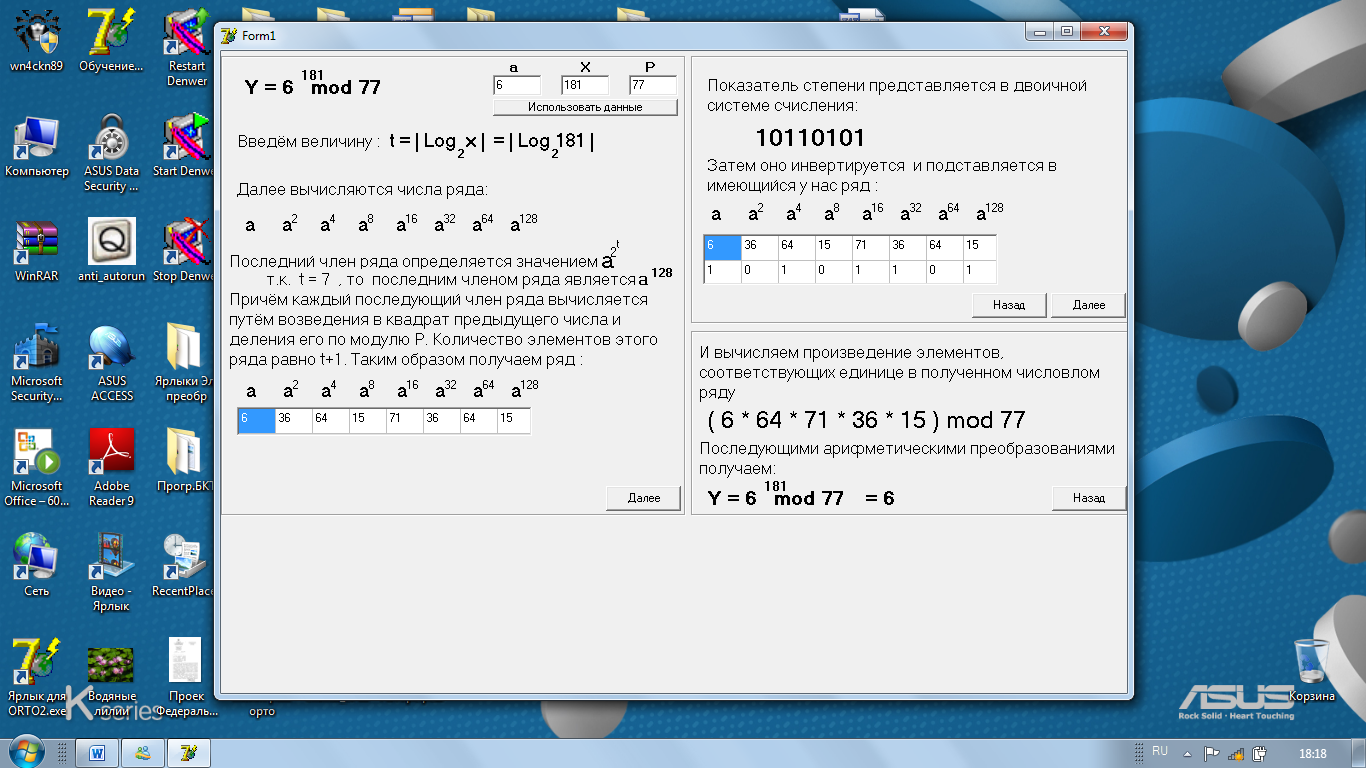
Рис.2. Пример решения задачи возведения числа по модулю.

2.4. Определение односторонней функции.

Важным элементом в системах криптографической защиты и аутентификации электронных сообщений является применение односторонних функций как при вычислении парных ключей шифрования-дешифрования (открытого ключа К_О и закрытого (секретного) ключа К_З) , так и при формировании электронной цифровой подписи.

В криптографических алгоритмах основными однонаправленными функциями являются:

- функция целочисленного умножения или как ее определяют функция факторизации (разложения на простые множители) больших чисел;

- модульная экспонента с фиксированным основанием и модулем или как ее обратное отображение - функция задачи дискретного логарифмирования.

Однако, в любом представлении однонаправленная функция определяется как:

- для любых произвольных множеств X и Y определено, что f : X → Y, т.е. существует функция однозначного преобразования элементов множества X во множество Y, устанавливается однозначное соответствие между элементами множества X и Y. Запись f : X → Y читается как «каждому элементу множества X ставится в однозначное соответствие элемент множества Y» или «функциональное преобразование (f) множества X (:) влечет за собой (→) множество Y.

Функция f : X → Y является однонаправленной, если для всех элементов x_i множества X (x_i є X) функция y_i = f(x_i) является легко вычисляемой для любого элемента y_i, принадлежащего множеству Y, т.е. y_iєY. Решение же обратной задачи при x_i є X и y_i є Y для однонаправленных функций должно быть вычислительно неразрешимой задачей, т.е. если y_i = f (x_i), то x_i ≠ f (y_i). В практической криптографии однонаправленным функциональным преобразованием для криптографической системы защиты и аутентификации электронных сообщений, построенным по алгоритму RSA (Райвест-Шамир-Адлеман) является вычисление произведения двух больших простых чисел (порядка 100 десятичных знаков). Прямое решение задачи, т.е. нахождение значения их произведения для современных вычислительных комплексов является достаточно простой задачей, т. е.

N = P * Q . Однако решение обратной задачи нахождения чисел P и Q заданного большого числа N является неразрешимой задачей (если разрядность чисел P и Q одинакова и каждое число содержит не менее 100 десятичных знаков).

Для криптографических систем с алгоритмом функционирования Эль Гамаля – модульная экспонента с фиксированным основанием и модулем – Y = a^X mod P, где: Р – большое простое число; а – целое число, причем а < Р; х – случайное целое число, причем х < Р.

Нахождение значения y_i = a^X mod P является достаточно простой задачей. Нахождение же обратного значения x_i = log_a y_i mod P, при значениях «а» и «Р» порядка 150 десятичных знаков является относительно неразрешимой задачей. Эту задачу называют задача дискретного логарифмирования, решение которой за приемлемое время невозможно, в соответствии с чем модульная экспонента относится к классу однонаправленных функций, что и определило ее широкое применение в криптографических системах защиты и аутентификации электронных сообщений в компьютерных технологиях.