7. Windows-кодирование.
На сегодняшний день наиболее распространенной исходной системой кодирования является Windows-кодирование, элементы кодовых комбинаций которой представлены в таблице 4.12.
Таблица 4.12
Windows-кодирование
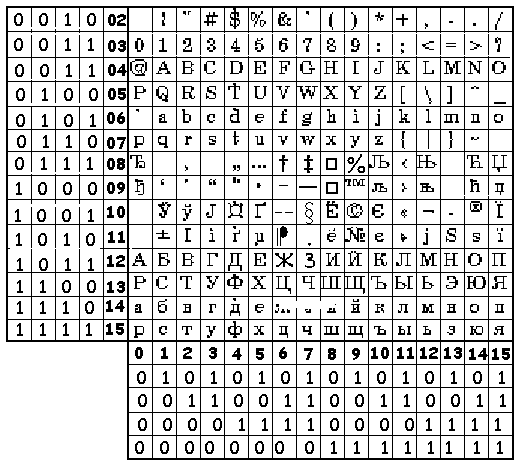
В приведенной таблице a0 ... a7 элементы кодовых комбинаций (a0-младший разряд, a7-старший разряд).
Для закрепления рассмотренного выше материала изучим процесс повышения достоверности и защиты информации от несанкционированного доступа с использованием преобразований исходных кодовых комбинаций Windows-кодирования (CP-1251) на множествах кодирования с обнаружением и исправлением искажений (коды Грея, систематические коды, коды Хэмминга, циклические коды, коды БЧХ).
7.1. Преобразование Windows-кодирования - коды Грея.
Исходный символ Исходная кодовая комбинация Код Грея
Т = 11001011 11001011
11001011
10101110
7.2. Преобразование Windows-кодирования в систематические коды.
Пример: построить систематический код с исправлением одиночных искажений S=1, с числом информационных элементов k=8.
1.Определение минимального кодового расстояния систематического dmin=2s+1=21+1=3.
2.Определение общего количества элементов систематического кода
Np
256
, откуда
n=13.
3.Определение числа проверочных элементов систематического кода r=n-k=13-8=5.
4.Из полного множества кодовых комбинаций, состоящих из 5 элементных кодов, выбираются 8 кодовых комбинаций, вес каждой из которых pdmin-1.
3 - 1 = 2 (00011, 00101, 00110, 01001, 01010, 01100, 11000).
5.Построение
производящей матрицы систематического
кода G
.
-
100000000 00011
010000000 00101
001000000 00110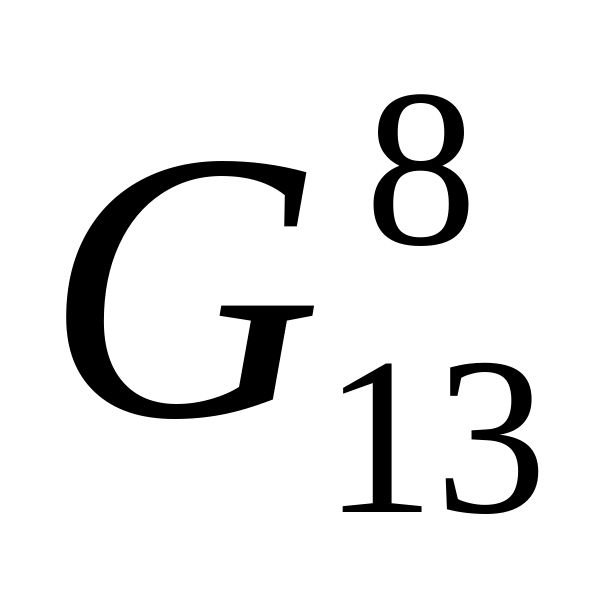
=000100000 01001
000010000 01010
00000100 011000
00000010 100100
00000001 110000
6.Определение r проверочных элементов по известным информационным элементам.
6.1.Построение проверочной матрицы H
Для построения проверочной матрицы H необходимо построить подматрицу D
-
00000011
D =
0001110101100100
10101010
11010000
-
a1a2a3 a4 a5 a6 a7 a8 b1 b2 b3 b4 b5
H =
0 0 0 0 0 0 1 1 1 0 0 0 00 0 0 1 1 1 0 1 0 1 0 0 0
0 1 1 0 0 1 0 1 0 0 1 0 0
1 0 1 0 1 0 1 0 0 0 0 1 0
1 1 0 1 0 0 0 0 0 0 0 0 1
По
полученной проверочной матрице H
определяются
проверочные элементы b
,
b
,
b
, b
,
b
b
=a
a
b
=a
a
a
a
b =a a a a (33)
b =a a a a
b =a a a
По полученным формулам из исходной кодовой комбинации Windows-кодирования образуется любая комбинация систематического кода, исправляющего одиночные искажения.
Например: букваТ русского алфавита в системе Windows-кодирования имеет вид
a a a a a a a a a1a2a3a4a5a6a7a8b1b2b3b4b5
Т 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 1 0 1
b1=1 0=1
b2=1 0 0 0=1
b3=1 0 0 0=1
b4=1 0 0 1=0
b5=1 1 1=1
В этом случае общий вид систематического кода при преобразовании семантического элемента Windows-кодирования имеет вид
Ni=a1a2a3a4a5a6a7a8b1b2b3b4b5 (34)
Преобразуя по полученным формулам (33, 34) исходные в системе Windows-кодирования двоичные кодовые комбинации семантического алфавита, получим полное множество его отображений в систематических кодах, обнаруживающих и исправляющих возникающие при их передаче по каналам связи искажения.
При декодировании принятых кодовых комбинаций систематического кода Windows-кодирования алгоритм распознавания искажений кодовых комбинаций определяется следующими уравнениями:
b
=b1
a7
a8
b
=b2
a4
a5
a6
a8
b
=b3
a2
a3
a6
a8
(35)
b
=b4
a1
a3
a5
a7
b
=b5
a1
a2
a4
Например при передаче Windows-кода буквы Т =110100101110 произошло искажение, и принята комбинация Т=1101011011101 (искажение в 6-ом разряде, передан 0 принята 1).
Определяем проверочные символы b ... b (в рассматриваемом примере a1=1,a2=1, a3=0, a4=1, a5=0, a6=1, a7=1, a8=0, b1=1, b2=1, b3=1, b4=0, b5=1).
b =1 1 0=0
b =1 1 0 1 0=1
b =1 1 0 1 0=1
b =0 1 0 0 1=0
b =1 1 1 1=0
Равенство уравнений b и b единице указывает, что при приеме произошло искажение. Искаженным может быть один из элементов b2, b3, a2, a3, a4, a5, a6, a8, но элементы a2, a3, a4, a5, a8 входят в уравнения b , b , b и искаженными быть не могут. Остается распознать элементы b2, b3, a6.
Элемент a6 входит в оба уравнения, содержащих искаженный элемент (b и b ), следовательно, он и искажен. Заменяя в элементе a6 значение 1 на 0, получим исправленную кодовую комбинацию Т = 1101001011101.