6.1.1. Систематические коды.

К систематическим кодам относят блочные разделимые n, k -коды, в которых проверочные элементы кодовых комбинаций представляют собой линейные комбинации информационных элементов. К систематическим кодам в частности относят коды Хэмминга, Циклические коды, которые нашли широкое практическое внедрение в цифровых системах кодирования и передачи информации.

Характерной особенностью непрерывных кодов является кодирование исходных сообщений таким образом, что проверочные элементы кодовых комбинаций размещаются среди информационных элементов и в этом случае происходит непрерывное кодирование и декодирование исходных сообщений.

Прежде чем приступить к рассмотрению методики формирования корректирующих кодовых комбинаций необходимо рассмотреть две основные характеристики корректирующих кодов - это избыточность корректирующего кода и кодовое расстояние. Характерной особенностью корректирующих кодов является их обязательная информационная избыточность за счет использования не всего множества состояний кодовых комбинаций, а только лишь выборочных комбинаций или так называемых разрешенных комбинаций. Очевидно, что количество разрешенных комбинаций меньше полного множества кодовых комбинаций N_p  N. Запрещенные комбинации N_з=N-N_р используются для обнаружения и исправления ошибок в разрешенных (информационных) кодовых комбинациях, которые могут возникнуть за счет возмущающего воздействия помех, действующих в линиях связи или преднамеренного созданного разрушающего воздействия.

В общем виде избыточность корректирующих кодов определится в соответствии со следующей формулой:

R = 1 - (11)

где: N - общее число комбинаций двоичного кода N= 2ⁿ;

N_р- число разрешенных кодовых комбинаций, предназначенных для кодирования передаваемых сообщений.

Из формулы (11) следует, что при отсутствии корректирующей способности кодовой комбинации, т.е. когда используется полное множество двоичных комбинаций для кодирования передаваемых сообщений, избыточность формируемой кодовой комбинации равна нулю, R=0.

Для того чтобы кодовые комбинации были распознаваемы, обладали способностью выявлять и исправлять возможные искажения, они по своему составу должны отличаться друг от друга на определенное кодовое расстояние. Под кодовым расстоянием между двумя кодовыми комбинациями понимают число равное количеству несовпадающих элементов этих комбинаций. Например, кодовое расстояние между кодами 01011011 и 10011110 равно 4. Наименьшее кодовое расстояние между двумя кодовыми комбинациями из всего рассматриваемого множества называют минимальным кодовым расстоянием и обозначают как d_min. Чем больше кодовое расстояние, тем большее количество искажений в кодовой комбинации можно обнаружить и исправить. Однако, при больших кодовых расстояниях резко уменьшается количество разрешенных кодовых комбинаций, т.е. увеличивается избыточность кодового множества.

6.1.2. Корректирующие коды с обнаружением искажений, применяемые в системах передачи и обработки информации.

Как было указано выше, корректирующие коды обладают способностью выявлять и исправлять ошибки, возникающие в их комбинациях. Воспринимающим и распознающим ошибки, возникающие в их комбинациях, устройством является синдром, который входит в состав приемника системы передачи данных.

Для обнаружения искажений кодовых комбинаций минимальное кодовое расстояние между отдельными кодовыми комбинациями определяется по следующей зависимости

d_min = t + 1 (12)

где: t - число обнаруживаемых искажений.

Согласно приведенной зависимости в случае искажения разрешенной кодовой комбинации эта модифицированная комбинация не будет совпадать ни с одной из комбинаций разрешенного множества. Следовательно, модифицированная комбинация будет принадлежать к запрещенному множеству и по ее структуре будет определяться характер и место искажения в разрешенной кодовой комбинации.

Например: для кодов 0000, 0011, 1010, 1101 минимальное кодовое расстояние d_min = 2. Если произошло искажение во второй комбинации 0011  0111, то условие минимального кодового расстояния d_min=2 для первой и второй кодовых комбинаций выполняться не будет d₁₂=3; d₃₂=3 и, следовательно, такая кодовая комбинация будет передана в синдром приемника для анализа и исправления.

Для исправления искажений, возникающих в принимаемых кодовых комбинациях, минимальное кодовое расстояние определяется из условия d_min=2S + 1 (13),

где S - число исправляемых искажений.

Как видно из зависимостей (12) и (13) для того, чтобы исправить кодовую комбинацию минимальное кодовое расстояние должно быть больше, чем в случае обнаружения искажения, а, следовательно, количество разрешенных кодовых комбинаций для кодирования сообщений уменьшится.

Процесс исправления искаженных кодовых комбинаций осуществляется следующим образом: принятая кодовая комбинация, подвергшаяся искажению, идентифицируется как запрещенная кодовая комбинация (по минимальному кодовому расстоянию для обнаружения искажений) сравнивается с частным множеством разрешенных кодовых комбинаций (неискаженных) и вычисляется та, которая отличается от принятой (искаженной) наименьшим кодовым расстоянием. Эта комбинация и считается достоверной. При работе синдрома только на обнаружение возможных искажений исправление принятых кодовых комбинаций не происходит и "он принимает решение о запрете" обработки такой кодовой комбинации.

При использовании корректирующих кодов для обнаружения и одновременного исправления возникших искажений необходимо выполнение следующего условия:

d_min = t + S +1 (14)

где: t - количество обнаруживаемых искажений;

S - количество исправляемых искажений;

t  S , т.е. число обнаруживаемых искажений больше чем исправляемых.

Примером распространенного множества кодовых комбинаций, способных выявить возникающие искажения, является множество кодов на одно сочетание. В кодах на одно сочетание каждая кодовая комбинация имеет постоянное число элементов с характерным признаком k. Например таким характерным признаком может быть наличие в каждой кодовой комбинации разрешенного множества строго детерминированного количества единиц (k=2, k=3).

В таблице 4.6 приведено разрешенное множество таких комбинаций из полного множества кодовых комбинаций, состоящих из 5 элементов.

Таблица 4.6

Коды на одно сочетание

N п/п	k = 2	k = 3
0	00011	00111
1	00101	01011
2	00110	01101
3	01001	01110
4	01010	10011
5	01100	10101
6	10001	10110
7	10010	11001
8	10100	11010
9	11000	11100

В таком множестве кодовых комбинаций, каждая из которых состоит из n элементов, количество элементов с характерным признаком k для всех кодовых комбинаций разрешенного множества одно и то же (количество единиц в кодовой комбинации). В этом случае объем разрешенного множества определяется сочетанием из n элементов по k.

N_p = C = (15)

Максимальное количество кодовых комбинаций разрешенное множество N_p будет иметь при следующих условиях, если n четно, то k необходимо принять k= ; если n нечетно, то k= или k= .

Например , определить максимальное количество кодовых комбинаций разрешенного множества при числе элементов кодовых комбинаций равное 5, т.е. при n=5 определить k и N_p.

k= = =2; k= =3;

N_p=C = =10; N_p=C = =10.

Как видно, при вычислении k по первому и второму способу объем разрешенной выборки кодового множества не меняется.

Разрешенное множество кодовых комбинаций с обнаружением ошибок с применением кодов на одно сочетание строится следующим образом:

строится множество двоичных кодов на все сочетания N=2ⁿ, из всего множества выбираются только те кодовые комбинации, для которых характерный признак k один и тот же.

В рассмотренном выше примере таким характерным признаком является наличие постоянного числа единиц в разрешенных кодовых комбинациях (k=2; k=3). Это множество приведено в таблице 5. Анализ кодовых комбинаций на одно сочетание показал, что для них минимальное кодовое расстояние d_min=2. В этих кодах возможно обнаружение одной и более ошибок, т.к. искажения в кодовых комбинациях приводят к изменению характерного признака конкретного кодового множества. Так для случаев k=2 и k=3 появление в кодовых комбинациях соответствующих искажений (10, 01) приводит к изменению числа единиц в разрешенных кодовых комбинациях, что и будет говорить о наличии искажений.

Избыточность кодов на одно сочетание определится из соотношения

R = 1 - = 1 - (16)

Из таблицы 4.6 следует:

R = 1 -  0,35, d = 2, t = 1.

Другой разновидностью корректирующих кодов с обнаружением искажений являются коды с четным или нечетным числом единиц. При формировании двоичных кодовых множеств с четным (нечетным) числом единиц из всего 2ⁿ множества выбирают соответствующие кодовые комбинации, полученное разрешенное множество будет содержать N_p= =2^n-1 кодовых комбинаций, т.к. минимальное кодовое расстояние равно d=2, то такие коды способны обнаруживать одиночные искажения т.к. t = d_min - 1 = 1. Последнее равенство справедливо при условии, если в неискаженных разрешенных комбинациях число единиц четное (нечетное), и изменение одного из элементов кодовой комбинации приводит к нарушению четности (нечетности), что и позволяет судить о возникшем искажении.

Избыточность таких кодов определится как R=1- =1 - =

= при n = 4 избыточность составляет R = 0,25, т.е. коды с четным или нечетным числом единиц обладают меньшей избыточностью по сравнению с кодами на одно сочетание, а, следовательно, при одном и том же числе кодовых элементов можно получить большее количество кодовых комбинаций для кодирования исходного сообщения.

Коды с повторением также являются разновидностью корректирующих кодов с обнаружением ошибок. Эти коды строятся из исходного кода путем его дополнения аналогичной кодовой комбинацией (т.е. происходит повторение передаваемой кодовой комбинации дважды).

Например: исходная комбинация 0101, передаваемая двоичная комбинация имеет вид 01010101. Кодовая комбинация, принимаемая приемным декодирующим устройством, считается достоверной, если в дополненной кодовой комбинации исходня часть совпадает с дополненной. Избыточность таких кодов равна:

R = 1 - = 1 - = 0,5.

Коды с удвоением элементов. Эти коды также принадлежат ко множеству корректирующих кодов с обнаружением искажений, они образуются в результате удвоения каждого элемента исходной кодовой комбинации, причем нуль в исходной комбинации заменяется на два элемента 01, а единица на 10. Например, исходная кодовая комбинация имеет вид 0101, удвоенная (передаваемая по линии связи) 01100110. В передаваемых кодовых комбинациях парные соседние элементы имеют только два вида 01 или 10 и появление парных элементов в принимаемых кодовых комбинациях вида 00 или 11 будет говорить о возникших искажениях. Сформированные таким образом кодовые комбинации имеют в два раза больше элементов чем исходные, следовательно, они обладают большей избыточностью. Избыточность таких кодов определится как

R = 1 - = 1 - = 0,5.

Большой класс корректирующих кодов составляет множество систематических кодов, которые определены как блочные разделимые n, k - коды. В таких кодах, состоящих из n символьных элементов, k элементов являются информационными, а оставшиеся r=n-k элементов кодовых комбинаций проверочными. Проверочные элементы образуются с помощью линейных преобразований информационных кодовых комбинаций [6].

Как правило, систематические коды (n, k - коды) структурно составляются таким образом, что первое подмножество кодовой комбинации состоит из информационных элементов, а следующее за ним подмножество элементов кода состоит из проверочных элементов.

Построение кодовых комбинаций блочных разделимых кодов базируется на двух леммах:

1. Суммирование по модулю 2 любого множества разрешенных комбинаций также дает разрешенную комбинацию.

2. Минимальное кодовое расстояние систематического кода равно минимальному весу его ненулевых кодовых комбинаций (весом кодовой комбинации называется число единиц этой кодовой комбинации).

Кодовые комбинации называются линейно независимыми, если соблюдается следующее условие c₁f₁ c₂f₂ ... с_kf_k 0 для всех возможных значений c_i (c_i=1  0). Исключение составляет случай, когда с₁ = с₂ = ... = с_к = 0.

Для образования полного множества линейно независимых кодовых комбинаций, согласно первому постулату, путем сложения по модулю 2 k линейно независимых комбинаций f₁, f₂, ... , f_k и придания значений 0 или 1 коэффициентам с_i получают N_p = 2^k разрешенных кодовых комбинаций систематического кода. Определенные для построения множества комбинаций систематического кода линейно независимые комбинации f₁, f₂, ... , f_k записываются друг под другом в виде матрицы G_n,k.

Такая матрица, состоящая из k строк и n столбцов, называется производящей матрицей n, k кода [7].

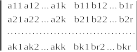
G_n,k = (17)

П роизводящая матрица представлена двумя подматрицами: информационной (a_ik) и проверочной (b_ir). Информационная матрица состоит из k столбцов, проверочная из r столбцов. В качестве информационной подматрицы производящей матрицы можно взять единичную матрицу E_k

1 0 ... 0

01 ... 0

E_,k = ........… (18)

0 0 ... 1

С учетом (17) и (18) производящая матрица для построения систематического кода будет иметь следующий вид:

1 0 ... 0 b₁₁ b₁₂ ... b_1r

0 1 ... 0 b₂₁ b₂₂ ... b_2r

G_n,k = .................................... (19)

0 0 ... 1 b_k1 b_k2 ... b_kr

…………………….

a₁a₂... a_k b₁ b₂ .... b_r

Проверочная подматрица строится на основе информационной подматрицы с учетом следующих положений. Так как каждая строка кодового множества информационной подматрицы (18) содержит только одну 1, то вес каждой строки проверочной подматрицы должен быть не менее p₁ = d_min - 1, сумма двух любых строк по модулю 2 не менее p₁₂ = d_min -2.

Алгоритм построения систематического кода определяется следующим образом:

Цель процесса алгоритмизации построить код исправляющий одиночные искажения (S=1) при числе разрешенных комбинаций (в качестве примера) N_p = 2⁵ = 32 и числе информационных элементов k = 5.

1. Определение минимального кодового расстояния

d_min = 2S + 1 = 21 + 1 = 3.

2. Определение общего количества элементов кодовых комбинаций систематического кода - n.

N_p = =

где: С - количество вариантов состояний кодовых комбинаций, когда искажение отсутствует (C = 1).

С - количество вариантов кодовых комбинаций, когда возникают одиночные искажения ( в рассматриваемом примере C = =n.

3. Из формулы для определения N_p определяют общее количество элементов систематического кода

2^k = ; 2⁵ = ; 32 =

при определении n выбирают минимальный верхний предел, т.е. sup n sup n = 9, т.к. 32 должно быть меньше или равно , то выбирая наименьший верхний предел, получают n=9, т.е. n=9; k=5.

4. Определение числа проверочных элементов систематического кода r = n - k = 9 - 5 = 4. Для случая r=4 строится множество кодовых комбинаций N_r = 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, !001, 1010, 1011, 1100, 1101, 1110, 1111.Из полученного множества для построения проверочной подматрицы производящей матрицы выбирают пять (к=5) комбинаций (любых), вес каждой из которых p d_min-1=3-1=2. Такое подмножество определится как N₅=0011, 0101, 0110, 0111, 1001, общее же количество комбинаций, удовлетворяющих условию p 2 имеет вид N_{p 2} = 0011, 0101, 0110,0111, 1001, 1010, 1011, 1100, 1101, 1110, 1111, т.е. N_{p 2}=12.

5. Построение производящей матрицы систематического кода-G_9,5

10000	0011
(20) G9,5 = 01000	0101
00100	0110
00010	0111
00001	1001

Из общего количества разрешенных комбинаций систематического кода, содержащего 5 информационных символов N_р=2⁵ =32, пять комбинаций уже определено , т.к. они входят в состав производящей матрицы G_9,5, шестая комбинация нулевая (все элементы равны 0), осталось найти 26 производных комбинаций, которые определяются на основе суммирования по модулю 2 строк производящей матрицы, т.е. осуществляется кодирование систематического кода.

Для определения r поверочных элементов по известным информационным элементам необходимо построить проверочную матрицу, состоящую из r строк и n столбцов.

Проверочная матрица строится на основе единичной матрицы путем приписывания к ней слева подматрицы D_k,r, содержащей k столбцов и r строк. Каждая строка подматрицы D_k,r соответствует столбцу поверочной подматрицы производящей матрицы G_n,k

b11 b21 ... bk1

b12 b22 ... bk2

....................

b1r b2r ... bkr

Таким образом, проверочная матрица будет иметь вид

b11 b21 ... bk1 10 ... 0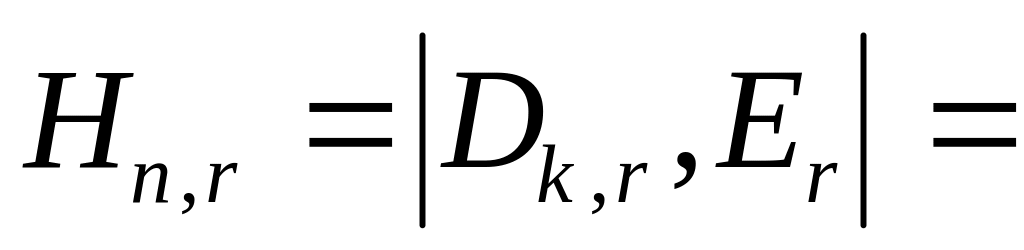

(22) b12 b22 ... bk2 01 ... 0

................................

b1r b2r ... bkr 00 ... 1

На основании проверочной матрицы H_n,r (22) формируется алгоритм кодирования и декодирования систематического кода.

В качестве примера построим на основании производящей матрицы (20) проверочную матрицу H_9,4.

		a1	a2	a3	a4	a5		b1	b2	b3	b4
(23)		0	0	0	0	1		1	0	0	0
H9,4	=	0	1	1	1	0		0	1	0	0
		1	0	1	1	0		0	0	1	0
		1	1	0	1	1		0	0	0	1

По полученной проверочной матрице H_9,4 определяются проверочные элементы b₁, b₂, b₃, b₄ на основании следующих уравнений:

b₁ = a₅

b₂ = a₂  a₃  a₄

b

(24)

₃ = a₁  a₃  a₄

b₄ = a₁  a₂  a₄  a₅

Следовательно, любая кодовая комбинация систематического кода определяется из N_p=2^k исходных комбинаций. Например, если на вход кодирующего устройства поступает исходная информационная кодовая комбинация 11001, то на его выходе образуется разрешенная кодовая комбинация систематического кода

a₁=1; a₂=1; a₃=0; a₄=0; a₅=1.

b₁=1; b₂=1; b₃=1; b₄=1.

11001  11001 1111.

При исходной комбинации 10101 кодовая комбинация систематического кода определится как

a₁=1; a₂=0; a₃=1; a₄=0; a₅=1.

b₁=1; b₂=1; b₃=0; b₄=0.

10101  10101 1100.

При декодировании принятых комбинаций, т.е. обработки систематического кода приемным устройством, алгоритм распознавания искаженной кодовой комбинации определяется в соответствии со следующими уравнениями:

b =b₁  a₅

b

(25)

=b₂  a₂  a₃  a₄

b =b₃  a₁  a₃  a₄

b =b₄  a₁  a₂  a₄  a₅

Например, при передаче разрешенной комбинации 110011111 произошло искажение в пятом разряде и принята комбинация 110001111 (искажение в 5 разряде, передана 1, а принят 0).

Если при проверке приемным устройством разрешенной комбинации систематического кода окажется, что хотя бы одно из уравнений (25) не будет равно 0, то в кодовой комбинации произошли ошибки. В приведенном примере принятая кодовая комбинация 110001111 по уравнениям (25) при a₁=1, a₂=1, a₃=0, a₄=0, a₅=0, b₁=1, b₂=1, b₃=1, b₄=1 оценивается как:

b =1  0 =1

b

(26)

=1  1  0  0=0

b =1  1  0  0=0

b =1  1  1  0  0=0

Равенство 1 первого и четвертого уравнений говорит о возникшем искажении кодовой комбинации и если стоит задача только оценки правильности приема кодовой комбинации, то по рассмотренному примеру формируется команда сигнализации об искажении принятой кодовой комбинации, принимается решение либо о перезапросе кодовой комбинации или об отказе ее обработке приемными устройствами.

Если же предусмотрена операция исправлений искажений, то необходимо провести дальнейший анализ уравнений (25).

Так например, наличие 1 в первом и четвертом уравнениях говорит о том, что искаженным может быть один из элементов разрешенной кодовой комбинации систематического кода b₁, b₄, a₁, a₂, a₄, a₅.

Наличие 0 во втором и третьем уравнениях означает, что элементы b₂, b₃, a₁, a₂, a₃, a₄ приняты без искажений. Исключая правильно принятые элементы из первого и четвертого уравнений определяют потенциально искаженные элементы. Таким искаженным элементом в рассматриваемом примере может быть один из b₁, b₄, a₅, но элемент a₅ входит и в первое и во второе уравнения, следовательно, искажен он.

Заменив в принятой кодовой комбинации в элементе 5 значение 0 на 1, восстанавливается искаженная кодовая комбинация. Результаты проверок правильности принятых кодовых комбинаций по уравнениям (25) называют синдромом (синдром-определитель), так же называется и программно-аппаратный модуль приемного устройства.

6.1.2.1. Код Хэмминга. Особенностью кода Хэмминга является то обстоятельство, что столбцы проверочной матрицы располагаются таким образом, что r-комбинация i-столбца соответствовала бы номеру i кодовой комбинации, записанному в двоичной форме. Такое расположение столбцов позволяет построить синдром таким образом, что его номер в двоичной форме будет указывать на номер искаженного элемента принятой кодовой комбинации. В качестве примера рассматривается проверочная матрица H_9,4 (23). По уравнениям (25) определяются синдромы одиночных искажений, их для наглядности удобно представить в виде таблицы 4.7 (на примере 10 элементной кодовой комбинации).

Таблица 4.7

Синдром одиночных искажений

Комбинация искажения	Номер искаженного элемента	Синдром
1000000000	1	0001
0100000000	2	0010
0010000000	3	0011
0001000000	4	0100
0000100000	5	0101
0000010000	6	0110
0000001000	7	0111
0000000100	8	1000
0000000010	9	1001
0000000001	10	1010

Как видно из приведенной таблицы кодовая комбинация синдрома указывает на искаженное место разрешенной кодовой комбинации. Например, если искажен пятый разряд разрешенной кодовой комбинации, то его синдром определится как 0101.

Преобразование исходных двоичных кодовых комбинаций во множество кодов Хэмминга целесообразно рассмотреть на конкретном примере.

Пример. Цель преобразования - составить Np=2ⁿ=60 разрешенных кодовых комбинаций Хэмминга, обнаруживающих и исправляющих одиночные искажения (t=1, S=1).

Методика решения.

1. Определение минимального кодового расстояния

d_min=t+S+1=1+1+1=3.

2. Определение общего числа элементов кодовых комбинаций Хэмминга - n.

N_p  ; 60 

Из последнего неравенства определяется общее число элементов кодовых комбинаций Хэмминга n=10.

3. Определение числа информационных элементов k

2^k = 60 k  6.

4. Определение числа проверочных элементов r

r = n - k = 10 - 6 = 4.

5. Построение производящей матрицы кода G_10,6 (10 столбцов, 6 строк). Для чего из состава 2^r = 2⁴ =16 проверочных комбинаций для построения производящей матрицы выбирается k=6 любых комбинаций с весом p  d_min- 1 = 3 - 1 = 2, например: 0011, 0101, 0110, 0111, 1001, 1010. Производящая матрица имеет вид:

1	0	0	0	0	0		0	0	1	1
0	1	0	0	0	0		0	1	0	1
G10,6 = 0	0	1	0	0	0		0	1	1	0
0	0	0	1	0	0		0	1	1	1
0	0	0	0	1	0		1	0	0	1
0	0	0	0	0	1		1	0	1	0

6. Построение проверочной матрицы на основании производящей матрицы G_10,6. Для чего в первую строку проверочной матрицы H_10,6 вписывается первый столбец кортежа проверочных элементов производящей матрицы G_10,7 (000011) и к нему справа приписывается первая строка единичной матрицы (1000), во вторую строку проверочной матрицы вписывается кортеж второго столбца производящей матрицы (011100) и справа приписывается вторая строка единичной матрицы (0100) и т. д. Причем необходимо отметить, что число элементов в строках производящей и проверочной матриц (n) одно и тоже, а количество строк проверочной матрицы равно числу проверочных элементов производящей матрицы.

a1	a2	a3	a4	a5	а6		b1	b2	b3	b4
H10,6 = 0	0	0	0	1	1		1	0	0	0
0	1	1	1	0	0		0	1	0	0
1	0	1	1	0	1		0	0	1	0
1	1	0	1	1	0		0	0	0	1

После чего для построения кода Хэмминга необходимо преобразовать проверочную матрицу перераспределением ее столбцов таким образом, чтобы кодовая комбинация кортежа столбцов указывала на номер столбца в проверочной матрице H_10,6.

e1	e2		e3				e4
u1	u2	u3	u4	u5	u6	u7	u8	u9	u10
H = 0	0	0	0	0	0	0	1	1	1
0	0	0	1	1	1	1	0	0	0
0	1	1	0	0	1	1	0	0	1
1	0	1	0	1	0	1	0	1	0

Таким образом, проверочная матрица H систематизирована в порядке возрастания номера столбца, причем столбцы u₁, u₂, u₄, u₈ являются столбцами единичной матрицы элементов исходной проверочной матрицы H_10,6.

7. По построенной проверочной матрицы H_10,6 составляются r=4 проверочных уравнений. Проверочные уравнения составляются в виде суммы по модулю 2 элементов строк матрицы H_10,6, элементы единичной матрицы которых равны 1.

e₁ = u₃  u₅  u₇  u₉

e

(27)

₂ = u₃  u₆  u₇  u₁₀

e₃ = u₅  u₆  u₇

e₄ = u₉  u₁₀

Полученные уравнения (27) являются исходными (кодообразующими) уравнениями для построения множества кодовых комбинаций кода Хэмминга. В рассмотренном примере на вход формирующего устройства (кодирующего) устройства поступает N_p=60 информационных комбинаций, а на его выходе образуется N_p=60 разрешенных комбинаций кода Хэмминга. Например: на вход кодирующего устройства поступает информационная комбинация 011001. В соответствии с уравнениями (27) u₃=0, u₅=1, u₆=1, u₇=0, u₉=0, u₁₀=1, элементы u₁, u₂, u₄, u₈ являются проверочными элементами e₁, e₂, e₃, e₄, значения которых и необходимо определить по формулам (27).

e₁=u₁=u₃  u₅  u₇  u₉ = 0  1  0  0 = 1

e₂=u₂=u₃  u₆  u₇  u₁₀ = 0  1  0  1 = 0

e₃=u₄=u₅  u₆  u₇ = 1  1  0 = 0

e₄=u₈=u₉  u₁₀ = 0  1 = 1

Таким образом, закодированная по коду Хэмминга разрешенная кодовая комбинация 011001, будет иметь вид:

e1	e2		e3				e4
u1	u2	u3	u4	u5	u6	u7	u8	u9	u10
1	0	0	0	1	1	0	1	0	1

Исходный код 011001  1000110101 Код Хэмминга

В таблице 4.8 приведен фрагмент кодирования исходных двоичных комбинаций по коду Хэмминга при N_p=60, обнаруживающего и исправляющего одиночные искажения (t=1, S=1).

Таблица 4.8

Кодирование по коду Хэмминга

Nп/п	Исходные информационные комбинации	Закодированные комбинации по Хэммингу
	u3 u5 u6 u7 u9 u10	e1 e2 e3 e4 u1 u2 u3 u4 u5 u6 u7 u8 u9 u10
1	0 0 0 0 0 1	0 1 0 0 0 0 0 1 0 1
2	0 0 0 0 1 0	1 0 0 0 0 0 0 1 1 0
3	0 0 0 0 1 1	1 1 0 0 0 0 0 0 1 1
4	0 0 0 1 0 0	1 1 0 1 0 0 1 0 0 0
5	0 0 0 1 0 1	1 0 0 1 0 0 1 1 0 1
6	0 0 0 1 1 0	0 1 0 1 0 0 1 1 1 0
7	0 0 0 1 1 1	0 0 0 1 0 0 1 0 1 1
8	0 0 1 0 0 0	0 1 0 1 0 1 0 0 0 0
9	0 0 1 0 0 1	0 0 0 1 0 1 0 1 0 1
.........	...................................	.............................................
58	1 1 1 0 1 0	1 0 1 0 1 1 0 1 1 0
59	1 1 1 0 1 1	1 1 1 0 1 1 0 0 1 1
60	1 1 1 1 0 0	1 1 1 1 1 1 1 0 0 0

Декодирование принятых комбинаций кода Хэмминга и исправление одиночных искажений производится в соответствии со следующими преобразованиями.

1. Определение элементов синдрома e , e , e , e

e = u₁ u₃ u₅ u₇ u₉

e

(28)

= u₂ u₃ u₆ u₇ u₁₀

e = u₄ u₅ u₆ u₇

e = u₈ u₉ u₁₀

2. Восстановление искаженной принятой кодовой комбинации кода Хэмминга. Пример: передается разрешенная комбинация кода Хэмминга 1001001101 в исходной информационной двоичной комбинации произошло искажение в третьем (слева направо) разряде искажение и на приемник поступил код 1011001101. Каждый разряд слева направо обозначается буквами u₁u₂u₃u₄u₅u₆u₇u₈u₉u₁₀. Декодирование осуществляется по системе уравнений (28):

e = 1  1  0  1  0 =1

e = 0  1  0  1  1 =1

e = 1  0  0  1 =0

e = 1  0  1 =0

Синдром в этом случае равен 0011, что при переводе в десятичное число означает цифру 3, т.е. 0011  3, это указывает на искажение третьего элемента в принятой кодовой комбинации, который и подлежит исправлению с 1 на 0, что в свою очередь и приводит к восстановлению искаженной кодовой комбинации.

6.1.2.2. Циклические коды. Другой разновидностью систематических кодов являются циклические коды, которые отличаются высокой корректирующей способностью и сравнительной простотой технической реализации.

Название циклических кодов определилось с учетом того, что множество разрешенных комбинаций образуется в результате циклического сдвига. Отображение циклических кодов и выполнение отдельных операций над ними производят на основе степенных многочленов (полиномов) вида:

F(x) = a_n-1x^n-1 + a_n-2x^n-2 + ... + a₁x + a₀ (29)

где: x- основание системы счисления;

a₀, a₁, ..., a_n-1 - коэффициенты системы счисления в двоичной системе (0, 1).

Например, комбинация 100100110 отображается на многочлене (29) в виде:

100100110  1x⁸ + 0x⁷ + 0x⁶ + 1x⁵ + 0x⁴ + 0x³ + 1x² + 1x +0 =

= x⁸ + x⁵ + x² + x.

Преобразование кодовых комбинаций циклических кодов сводится к действиям сложения, умножения и деления над степенными многочленами.

1. Сложение (x⁵ + x⁴ + x² + 1) + (x⁴ + x³ + x² + x + 1)

x⁵ + x⁴ + 0 + x² + 0 + 1



0 + x⁴ + x³ + x² + x + 0

x⁵ + 0 + x³ + 0 + x + 1 = x⁵ + x³ + x + 1

2. Умножение (x⁴ + x² + x + 1) (x² + 1)

x⁴ + 0 + x² + x + 1



x²+ 1

x⁴ + 0 + x² + x + 1

x⁶+0+x⁴ + x³+ x²

x⁶+0+0 + x³ +0 + x + 1 = x⁶ + x³ + x + 1.

3. Деление (x⁵+x³+x²+1):(x+1)

x⁵+0+x³+x²+0+1 x+1

x⁵+x⁴ x⁴+x³+x+1

x⁴+x³+x²+0+1

x⁴+x³

x²+0+1

x²+x

x+1

x+1

0.

Прежде чем приступить к изложению материала по построению циклических кодов, необходимо привести их основные положения.

Циклическим кодом (n, k) называется систематический код, каждая комбинация которого делится без остатка на образующий многочлен P(x) степени r=n-k. Причем каждая кодовая комбинация циклического кода представляется в виде многочлена степени  n-1.

В качестве образующих многочленов P(x) используются неприводимые многочлены. Неприводимый многочлен это такой многочлен, который делится без остатка только на самого себя или на единицу.

В общем виде алгоритм построения циклических кодов может быть представлен в следующем виде:

1. Выбирается число информационных элементов циклического кода F(x).

2. Выбирается образующий многочлен P(x).

3. Каждая кодовая комбинация простого двоичного множества умножается на x^r (Q(x)x^r).

4. Полученное произведение делится на образующий многочлен P(x) , , находится частное G(x) и остаток R(x).

5. Определяется кодовый многочлен F(x) циклического кода

F(x) = Q(x)x^r + R(x) (30).

Например: построить кодовую комбинацию циклического кода F(x) с числом информационных элементов k=6. В качестве образующего многочлена определен многочлен вида P(x)=x³+x+1. В этом случае число проверочных элементов r=3 (определяется по степени образующего многочлена).

1. Общее число элементов кодовой комбинации циклического кода равно n=k+r=6+3=9.

2. Образующий многочлен P(x)=x³+x+1.

3. Выбирается комбинация простого двоичного числа исходного множества (любая) Q(x)=010111x⁴+x²+x+1 и определяется произведение Q(x)x^r=(x⁴+x²+x+1)x³=x⁷+x⁵+x⁴+x³.

4. Определение частного G(x) и остатка R(x)

G(x) + R(x) =

x⁷+x⁵+x⁴+x³ x³+x+1

x⁷+x⁵+x⁴ x⁴+1

0 + 0 +0 + x³

x³+x+1

x+1

Следовательно, G(x)=x⁴+1; R(x)=x+1.

В соответствии с формулой (30) определяется кодовый многочлен F(x) и кодовая комбинация циклического кода (9,6) в двоичной форме:

F(x)=Q(x)x^r+R(x)=(x⁷+x⁵+x⁴+x³)+(x+1)

F(0,1)=010111 011

где: 010111 - информационные элементы циклического кода k;

011 - проверочные элементы циклического кода r.

В таблице 4.9 приведен пример множества кодовых комбинаций циклического кода F(x)_9,6 при образующем многочлене P(x)=x³+x+1.

Образующий многочлен P(x)=x³+x+1; F(x)=Q(x)x^r+R(x)

Таблица 4.9

Кодовые комбинации циклического кода

Простой двоичный код Q(x)	Кодовый многочлен Q(x)	Q(x)xr	Остаток R(x)	Кодовая комбинация циклического кода
				двоичная форма F(1,0)	Кодовый многочлен F(x)
000001	1	x3	x+1	000001011	x3+x+1
000010	X	x4	x2+x	000010110	x4+x2+x
000011	x+1	x4+x3	x2+1	000011101	x4+x3+x2+1
000100	x2	x5	x2+x+1	000100111	x5+x2+x+1
000101	x2+1	x5+x3	x2	000101100	x5+x3+x2
000110	x2+x	x5+x4	1	000110001	x5+x4+1
000111	x2+x+1	x5+x4+x3	x	000111010	x5+x4+x3+x
001000	x3	x6	x2+1	001000101	x6+x2+1
001001	x3+1	x6+x3	x2+x	001001110	x6+x3+x2+x
001010	x3+x	x6+x4	x+1	001010011	x6+x4+x+1
001011	x3+x+1	x6+x4+x3	0	001011000	x6+x4+x3
001100	x3+x2	x6+x5	x	001100010	x6+x5+x
001101	x3+x2+1	x6+x5+x3	1	001101001	x6+x5+x3+1
001110	x3+x2+x	x6+x5+x4	x2	001110100	x6+x5+x4+x2
001111	x3+x2+x+1	x6+x5+x4+x3	x2+1	001111101	x6+x5+x4+x3+x2+1
010000	x4	x7	1	010000001	x7+1
010001	x4+1	x7+x3	x	010001010	x7+x3+x
010010	x4+x	x7+x4	x2+1	010010101	x7+x4+x2+1
010011	x4+x+1	x7+x4+x3	x2	010011100	x7+x4+x3+x2
010100	x4+x2	x7+x5	x2+x	010100110	x7+x5+x2+x
010101	x4+x2+1	x7+x5+x3	x2+1	010101101	x7+x5+x3+x2+1

Образующими многочленами при построении циклических кодов используются неприводимые многочлены, т.е. такие многочлены, которые делятся без остатка только на самого себя или единицу. Степень выбранного образующего многочлена должна равняться числу проверочных элементов r.

В таблице 4.10 приведены все неприводимые многочлены до шестой степени.

Таблица 4.10

Неприводимые многочлены

№	Вид неприводимого многочлена
1	x+1
2	x2+x+1
3	x3+x+1 x3+x2+1
4	x4+x+1 x4+x3+1 x4+x3+x2+x+1
5	x5+x2+1 x5+x3+1 x5+x3+x2+x+1 x5+x4+x2+x+1 x5+x4+x3+x+1 x5+x4+x3+x2+1
6	x6+x+1 x6+x3+1 x6+x4+x2+x+1 x6+x4+x3+x+1 x6+x5+1 x6+x5+x2+x+1 x6+x5+x3+x2+1 x6+x5+x4+x+1 x6+x5+x4+x2+1

Обнаружение и исправление одиночных искажений в циклических кодах при кодовом расстоянии d_min=3 осуществляется следующим образом:

1. Принятая комбинация циклического кода F^’(1,0) делится на образующий многочлен P(x), она считается достоверной, если остаток от деления равен нулю, в противном случае комбинация принята с искажением.

2. Определяется вес остатка p₀. При p₀  S принятая комбинация суммируется по модулю 2 с полученным остатком, образованная сумма определяет исправленную комбинацию (переданную комбинацию).

3. При p₀S производят циклический сдвиг принятой кодовой комбинации на один разряд влево. Полученная комбинация снова делится на образующий многочлен. Если в результате второго деления вес полученного остатка меньше или равен числу исправляемых искажений p₀ S, то делимое суммируется с остатком.

4. Производится циклический сдвиг полученной суммы на один разряд вправо. Образованная после сдвига кодовая комбинация м является восстановленной (исправленной) комбинацией.

5. Если в результате второго деления условие p₀ S не выполняется, то указанная операция продолжает выполняться до тех пор, пока не будет реализовано неравенство p₀ S.

6. Полученная кодовая комбинация в результате последнего циклического сдвига суммируется с остатком от деления этой комбинации на образующий многочлен.

7. Производится циклический сдвиг вправо на столько разрядов, на сколько была сдвинута суммируемая с последним остатком кодовая комбинация относительно принятой кодовой комбинации. В результате получают исправленную кодовую комбинацию.

Пример.

При передаче кодовой комбинации циклического кода, исправляющего одиночные ошибки, произошло искажение в пятом разряде. Передавалась кодовая комбинация 1100101, принятая кодовая комбинация имеет вид 1110101. В рассматриваемом примере число исправляемых искажений S=1, число информационных символов кодовой комбинации k=4, число проверочных символов r=3. Следовательно, образующий многочлен будет иметь вид P(x)=x³+x²+1.

Степень образующего многочлена определяется числом проверочных символов, а сам образующий многочлен выбирается из таблицы неприводимых многочленов, таблица 9. Причем многочлен может быть взят любым из подмножества многочленов третьей степени. Если степень образующего многочлена будет иной, то и подмножество многочленов выбирается из подкласса рассматриваемой степени.

1. Деление принятой кодовой комбинации на образующий многочлен P(x)=x³+x²+1  1101.

1110101  1101

1101

1110

1101

111  остаток p₀=3.

2. При сравнении веса остатка (p₀=3) с числом исправляемых искажений S=1, имеем p₀  S. Условие p₀  S не выполняется.

3. Производится циклический сдвиг принятой кодовой комбинации на один разряд влево и повторное деление на образующий многочлен P(x).

1101011  1101

1101

011  остаток (вес остатка p₀=2). Условие p₀S не выполняется.

4. Сдвиг поразрядно влево и деление на образующий многочлен осуществляется до тех пор пока не будет выполнено условие p₀S.

1010111  1101

1101

1111

1101

1011

1101

110  остаток p₀=2S

0101111 1101

1101

1101

1101

1  остаток p₀=1=S. Условие p₀S выполнено.

5.При суммировании по модулю 2 последнего делимого 0101111 с остатком, получают комбинацию

0101111



1

0101110

6. Производится циклический сдвиг вправо полученной комбинации на 3 разряда (т.к. трижды при делении на образующий многочлен влево сдвигалась принятая кодовая комбинация).

0101110  0010111  10011  1100101.

Последняя кодовая комбинация полностью совпадает с переданной неискаженной кодовой комбинацией, т.е. произошло исправление принятой с искажением кодовой комбинации.

6.1.2.3. Коды Боуза-Чоудхури-Хоквингема (БЧХ) – относятся к классу циклических кодов и по своей разрешающей способности позволяют обнаруживать и исправлять два и более искажений кодовых комбинаций, возникающих при их передаче по каналам связи. Для таких кодов кодовое расстояние определяется как d_min5. Образующий многочлен построения множества кодовых комбинаций кодов БЧХ формируется на основании заданного количества кодовых комбинаций n, которое в сою очередь определяется полным множеством кодовых комбинаций кодов БЧХ - N и по числу исправляемых искажений S. Число элементов кодовой комбинации БЧХ определяется как n=2^m-1, где m - любое целое число (3, 4, 5, ...), число проверочных элементов кодовой комбинации выбирается из условия r mS = (log₂(n+1))S, а число информационных элементов будет равно k=n-r.

Образующий многочлен P(x) кода БЧХ представляет собой произведение нечетных минимальных многочленов m_i(x) и является их наименьшим общим кратным (НОК), т.е. наименьшим многочленом который без остатка делится на каждый минимальный многочлен m_i(x), где i=(1, 3, 5, ..., (2S-1)). Порядок многочлена P(x) равняется наименьшему общему кратному P(x)=НОКm₁(x) m₃(x) ... m_2S-1(x). Значения минимальных многочленов приведены в таблице 4.11.

Таблица 4.11

Коды минимальных многочленов

Ппорядок многочлена i	Минимальные многочлены при величине степени m
	2	3	4	5	6	7	8	9
1	1111	1011	10011	100101	1000011	10001001	100011101	100001001
3		1101	11111	111101	1010111	10001111	101110111	1001011001
5			111	110111	1100111	10011101	111110011	1100110001
7			11001	101111	1001001	11110111	101101001	1010011001
9				110111	1101	10111111	110111101	1100010011
11				111011	1101101	11010101	111100111	1000101101
13						10000011	100101011	1001110111
15							111010111	1101100001
17							010011	1011011001
19						11001011	101100101	1110000101
21						11100101	110001011	1000010111
23							101100011	1111101001
25							100011011	1111100011
27							100111111	1110001111
29								1101101011

Образующий многочлен с общим числом элементов n=2^m-1 и с числом исправляющий искажений S строится следующим образом. Из таблицы 4.11 выписываются все значения минимальных многочленов, соответствующих выбранному m до порядка 2S-1. Если в таблице такого числа нет, то выбирается минимальный нижний предел.

Например: цель - построить код БЧХ с общим числом элементов кодовой комбинации n=15, и исправляющим двойные искажения S=2.

1. Из формулы n=2^m-1 определяется m

2^m = n+1 по определению логарифма m=log₂(n+1)=log₂(15+1)=4.

Следовательно, общий вид образующего многочлена имеет вид:

P(x)=m₁(x) m₃(x) ... m_2S-1(x)=m₁(x) m₃(x).

2. Из таблицы 9 столбца m=4 выбирают многочлены для i=1 и i=3, т.е. m₁=10011, m₃=11111 откуда: m₁=x⁴+x+1, m₃=x⁴+x³+x²+x+1

3. Определяют вид образующего многочлена

P(x) = m₁(x)  m₃(x) = 100111111 = 111010001 = x⁸+x⁷+x⁶+x⁴+1

4. Определяют число проверочных и информационных элементов кодовых комбинаций кодов БЧХ: число проверочных элементов rmS=42=8; число информационных элементов k=n-r=15-8=7.

5. Строят дополнительную матрицу G_8,7 производящей матрицы G_15,7. Дополнительная матрица G_8,7 образуется делением единицы на кодовую комбинацию образующего многочлена P(x)=111010001

1 00000000 111010001

1 11010001

11010001 = R₁(x)

110100010

111010001

01110011 = R₂(x)

11100110 = R₃ (x)

111001100

111010001

00011101 = R₄(x)

00111010 = R₅(x)

01110100 = R₆(x)

11101000 = R₇(x)

6. Определяют производящую матрицу G_15,7

0000001 11010001

0000010 01110011

0000100 11100110

G_15,7 = 0001000 00011101

0010000 00111010

0100000 01110100

1000000 11101000

7. Строки производящей матрицы составляют подмножество множества кодовых комбинаций кодов БЧХ, остальные кодовые комбинации кодов БЧХ определяют по матрице G_15,7 сложением по модулю 2 всех возможных строк производящей матрицы.

Общее число множества кодовых комбинаций кода БЧХ для рассмотренного случая определится как N=2^k=2⁷=128.

Например из 1-ой и 2-ой кодовых комбинаций производящей матрицы получают следующую кодовую комбинацию кодов БЧХ

0000001 11010001



0000010 01110011

N₃= 0000011 10100010 и т.д.

Для примера целесообразно рассмотреть построение множества кодов БЧХ и для случая обнаружения и исправления тройных искажений в кодовых комбинациях. Ставится задача - построить множество кодовых комбинаций кодов БЧХ с общим числом элементов n=15 и количестве исправляемых искажений равных 3 (S=3).

1. Определяем степень минимальных многочленов m для построения образующего многочлена P(x)

m = log₂(n+1) = log₂16 = 4.

Следовательно образующий многочлен будет иметь вид:

P(x) = m₁(x) m₃(x) ... m_2S-1(x) = m₁(x) m₃(x) m₅(x)

2. Из таблицы 9 (столбец m=4) выбирают три минимальных многочлена с i=1,3,5 m₁(x)=10011=x⁴+x+1, m₃(x)=11111=x⁴+x³+x²+x+1,

m₅(x)=111=x²⁺x+1

3. Образующий многочлен для рассматриваемого примера определится как P(x)=m₁(x) m₃(x) m₅(x)=10011  11111 111=10100110111 x¹⁰+x⁸+x⁵+x⁴+x²+x+1.

4. Число проверочных элементов кодовых комбинаций r определится следующим образом rm S=43=12, но так как степень образующего многочлена P(x) равна 10, то r выбирается равным 10, r=10.

5. Число информационных элементов кода БЧХ определится как k=n-r (k=15-10=5).

6. По образующему многочлену P(x) строится дополнительная матрица G_10,5 производящей матрицы G_15,5. Строки дополнительной матрицы G_10,5 определяются в результате получения остатков от деления 1 с приписанными справа нулями на образующий многочлен P(X)=10100110111, таких остатков должно образоваться 5, т.к. число кодовых комбинаций остатка равно числу проверочных элементов r (r=10).

7. По дополнительной матрице G_10,5 строится производящая матрица G_15,5. Число строк такой матрицы также равно 5 (т.е. количеству информационных элементов k=5).

8. По образующей матрице путем суммирования ее строк определяются остальные кодовые комбинации множества кодов БЧХ, состоящих из 15 элементов и исправляющих тройные искажения.

Процесс построения дополнительной и производящей матриц, как и процесс формирования множества кодов БЧХ описан в предыдущем примере.

Для обнаружения и исправления искажений в кодовых комбинациях БЧХ алгоритм функционирования синдрома приемного устройства аналогичен алгоритму обнаружения и исправления искажений в простейших циклических кодах с минимальным кодовым расстоянием d_min2S+1.

Алгоритм обработки и исправления искажений кодовой комбинации кодов БЧХ целесообразно рассмотреть на конкретном примере.

Пример. Цель - произвести исправление двойного искажения (S=2) в принятой кодовой комбинации кода БЧХ с общим числом элементов n=15 и числом информационных элементов k=7.

Для примера построим кодовую комбинацию множества кодов БЧХ на основании производящей матрицы G_15,7. рассмотренной несколько выше. Сложением по модулю 2 трех строк производящей матрицы G_15,7 образуется следующая кодовая комбинация кода БЧХ

001000000111010

 010000001110100

100000011101000

111000010100110

Предположим, что при передаче кодовой комбинации кодов БЧХ N_i(1,0) = 111000010100110 произошло двойное искажение в двух соседних элементах (3 и 4 элементы младших разрядов). Принятая кодовая комбинация будет иметь вид N_i(1,0)=111000010101010.

Для исправления искажений в принятой кодовой комбинации необходимо принятую комбинацию разделить на образующий многочлен P(x)=P(1,0)=111010001. Образующий многочлен взят из приведенного примера, где и описано его построение.

11100010101010 111010001

111010001

100111010

111010001

111010111

111010001

1100  остаток p = S = 2,

т.е. вес остатка равен числу исправляемых искажений. Напоминаем, что для нахождения искаженных элементов кодовых комбинаций кодов БЧХ и их исправлений необходимо выполнение условия, чтобы вес остатка (количество единиц в остатке) был меньше или равен числу исправляемых искажений, т.е. pS. После чего принятая комбинация суммируется с полученным остатком по модулю 2. Полученная сумма и даст исправленную кодовую комбинацию. Если pS, то производится циклический сдвиг принятой комбинации на один разряд влево, и вновь образованная кодовая комбинация делится на образующий многочлен. Эта операция повторяется до тех пор, пока не будет выполняться условие pS. Затем производится последовательно сдвиг последней кодовой комбинации вправо на столько разрядов, на сколько была сдвинута влево искаженная кодовая комбинация. В результате циклического сдвига образуется исправленная кодовая комбинация.

Итак, в рассмотренном примере вес остатка равен числу исправляемых искажений (p=S=2), что удовлетворяет условию pS. Производя суммирование по модулю 2 принятой искаженной кодовой комбинации с полученным остатком, производится исправление искажений

111000010101010



1100

111000010100110  исправленная комбинация.

Для получения полной картины исправления искажений необходимо рассмотреть несколько вариантов.

Допустим, что искажены не соседние разряды кодовой комбинации кодов БЧХ, а первый и шестой, т.е. принятая кодовая комбинация будет иметь вид 111000010000111.

111000010000111 111010001

111010001

100110001

111010001

111000001

111010001

100001  остаток p=2.

Условие p  S выполняется, производится суммирование остатка с принятой кодовой комбинацией

111000010000111

 100001

111000010100110  исправленная комбинация.

При искажении пятого и тринадцатого элементов принятой комбинации алгоритм исправления определится как принятая искаженная комбинация 110000010110110

110000010110110 111010001

111010001

101001111

111010001

100111100

111010001

111011011

111010001

101010  остаток p=3 S

Производится сдвиг принятой кодовой комбинации (искаженной) 110000010110110 на один разряд влево, получаем 100000101101101. Производим деление вновь образованной кодовой комбинации на образующий многочлен.

100000101101101 111010001

111010001

110101001

111010001

111100001

111010001

110000101

111010001

1010100  остаток p=3S.

Повторяем операцию сдвига еще раз 000001011011011

000001011011011 111010001

111010001

101111001

111010001

10101000  остаток p=3S.

Т.к. pS кодовая комбинация 000001011011011 сдвигается еще на один разряд влево, получают 000010110110110.

000010110110110 111010001

111010001

101111001

111010001

101010000

111010001

10000001  остаток p=2=S.

Условие pS выполняется, т.к. S=2.

Производится сложение по модулю 2 сдвинутой на 3 разряда влево принятой искаженной кодовой комбинации 000010110110110 с последним остатком 10000001.

000010110110110

 10000001

000010100110111

Производим трехкратный сдвиг вправо результата суммирования 000010100110111. В результате такого сдвига получают исправленную кодовую комбинацию, переданную с передающего комплекта системы передачи данных, функционирующей в кодовом множестве БЧХ.

000010100110111  100001010011011  110000101001101  111000010100110 (исправленная кодовая комбинация)

Рассмотренные методы кодирования и декодирования информации являются типичными представителями средств и методов кодирования информации с обнаружением и исправлением ошибок в цифровых системах связи. При передаче информации по каналу с помехами (реальный случай) всегда существует вероятность того, что принятые данные будут содержать ошибки, вследствие чего устанавливается определенный уровень частоты появления ошибок, при превышении которого переданные данные считаются недостоверными и для дальнейшей обработки их использовать нельзя. Если частота ошибок в принимаемых данных превышает допустимый уровень, то в этом случае применяют системы кодирования с обнаружением и исправлением ошибок, которые повышают достоверность принимаемой информации.

Способность корректирующего кодирования была доказана еще в работах Шенона, он показал, что если пропускная способность канала больше скорости создания сообщений источником, то при использовании эффективных систем кодирования и декодирования можно вести передачу по каналам с шумами со сколь угодно малой вероятностью ошибок, т.е. в работах Шеннона показано, что мощность сигнала, помехи и полоса частот ограничивают лишь скорость передачи информации, а не ее точность.

Наряду с построением систем помехоустойчивого кодирования рассмотренные методы нашли свое применение и в системах защиты информации от несанкционированного доступа. Например, ключом кодовой защиты в циклических кодах является выбор образующего многочлена, с помощью которого происходит преобразование исходного двоичного кода систем первичного кодирования. В этом случае мощность множества ключей кодирования возрастает с увеличением степени образующего многочлена, т.е. с увеличением числа информационных и проверочных элементов, что и определяет степень устойчивости кодовых комбинаций к несанкционированному распознаванию.

Однако, прежде чем перейти к вопросам защиты информации от несанкционированного доступа, необходимо рассмотреть методы формирования исходных кодовых комбинаций, применяемых в современных вычислительных системах. Примером такого исходного кодирования является преобразование семантического алфавита в операционных оболочках Windows, определяемые как кодирование по стандарту CP-1251 или Windows-кодирование. Эта система кодирования не содержит символы псевдографики и получила в настоящее время наибольшее распространение как в локальных, так распределенных и глобальных системах типа Internet. При применении указанной системы кодирования семантического алфавита, каждый символ алфавита кодируется 8-битовой двоичной комбинацией. Однако, применение системы 8-битового кодирования имеет существенный недостаток, т.к. не обеспечивает кодирование символов алфавитов азиатских стран.

В настоящее время для обмена информацией на языках всех стран мира создается универсальная система кодирования UNICODE. В ее основе заложено 16-битовое кодирование. Т.е. каждый символ естественного алфавита, на каком бы языке стран мира он не отображался, представляет собой 16-разрядную кодовую комбинацию. В этом случае общее число кодовых комбинаций составит N=2ⁿ=2¹⁶=65536. Такое количество кодовых комбинаций позволяет кодировать даже полные наборы иероглифов всех восточных и арабских языков, а также все математические и химические символы. Такие системы кодирования не требует включения в набор сервисных программ-программ перекодирования естественных символов с одного стандарта на другой.