4.4. Алгоритм электронной цифровой подписи гост р34.10-94. (Отечественный стандарт электронной цифровой подписи).

Федеральный Закон №1 от 10 января 2002 года «Об электронной цифровой подписи» объявил о принятии на эксплуатацию в сетевых компьютерных технологиях государственных и частнопредпринимательских организаций и предприятий системы аутентификации электронных сообщений, реализованной в соответствии с ГОСТ Р34.10-2001. Однако, ряд систем, находящихся на эксплуатации в банковских системах, системах управления производственными технологическими процессами, системах государственного административного управления, построено в соответствии с ГОСТ Р34.10-94.

Системы аутентификации электронных сообщений, реализованные в соответствии с ГОСТ Р34.10-2001, являются модификацией систем, реализованных в соответствии с ГОСТ Р34.10-94 поэтому целесообразно изначально рассмотреть алгоритм функционирования ЭЦП по ГОСТ Р34.10-94, а затем перейти к изучению алгоритма ГОСТ Р34.10-2001.

Необходимо отметить, что алгоритм цифровой подписи, определяемый стандартом ГОСТ Р34.10-94, по построению и функционированию во многом совпадает с алгоритмом аутентификации DSA.

Действия абонента-отправителя электронного сообщения по формированию электронной цифровой подписи.

1. Абонент-отправитель случайным образом выбирает большое простое число «Р» и простое число «q», которое является делителем числа (Р-1).

Размер чисел «Р» и «q» составляет 512 < L < 1024 бит. Для примера выбираются следующие числа: Р = 887; q = 443.

2. На втором шаге алгоритмизации абонент-отправитель задает случайным образом целое число «а» при соблюдении следующих ограничений:

а < (Р-1) и а^q mod P = 1. Для примера число «а» принимается равным а = 16 (16⁴⁴³ mod 887 = 1 mod 887 → 1).

3. После определения чисел P; q; a случайным образом задается значение закрытого (секретного) ключа абонента-отправителя при условии, что его значение должно быть целым числом меньше значения числа q (1<К_ЗА<q). В заданном примере закрытый ключ принимается равным К_ЗА =312.

4. По заданному случайным образом числовому значению закрытого ключа абонент-отправитель производит вычисление значения своего открытого ключа по следующей зависимости: К_ОА = mod P.

По приведенному примеру это значение определится как:

К_ОА = 16³¹² mod 887 = 38404760576 mod 887 = 482 mod 887 → 482.

Следовательно, значение открытого ключа абонента-отправителя (абонента А) определяется как: К_ОА = 482.

5. Открытыми параметрами системы аутентификации электронных сообщений являются параметры P; q; a; К_ОА (в числовом примере эти параметры определены как: P = 887; q = 443; a = 16; К_ОА = 482). Числовые значения этих параметров передаются по открытым каналам телекоммуникаций всем абонентам корпоративной информационной системы для реализации функции проверки ЭЦП – установления достоверности принимаемого сообщения «М», т.е. для выполнения процесса аутентификации сообщения «М» абонентом-получателем (абонентом В).

6. Далее абонент-отправитель вычисляет значение функции хеширования передаваемого им сообщения «М» → h(M)^в. Для примера в качестве сообщения «М» задается слово «Криптон».

h(M)^в → {52 48 52 48 50 42 46 46 40 56 48 48 50 54 46 42 52 56 56 52 50 50 50 50 44 52 48 48 54 50 46 42}.

7. Для составления криптограммы числовых значений функции хеширования h(M)^в абонент-отправитель случайным образом задает число «к» при соблюдении условия ограничения 1 < к < q (для примера 1 < к < 443). Принимается значение к = 347.

8. На следующем шаге алгоритмизации производится вычисление значения параметра «r» в соответствии со следующей зависимостью:

r = (a^к mod P) mod q

Для принятых значений P=887; q=443; a=16; к=347 значение параметра «r» определится как: r = (16³⁴⁷ mod 887) mod 443 = (26 mod 887) mod 443 = = 26 mod 443 → 26. Параметр ЭЦП «r» является постоянным для всего множества числовых значений элементов функции хеширования сообщения «М».

9. После вычисления параметра ЭЦП «r» абонент-отправитель сообщения «М» производит шифрование каждого элемента функции хеширования h(M)^в с помощью закрытого (секретного) ключа К_ЗА абонента-отправителя в соответствии со следующей зависимостью:

S_i = (m_i * к + r * К_ЗА) mod q

По принятым для примера и вычисленным значениям m_i; к; r; К_ЗА вычисляются значения S_i для функции хеширования подписываемого сообщения «М» → «Криптон»:

S_i = (m_i * 347 + 26 * 312) mod 443

Где: m_i – числовые значения элементов функции хеширования сообщения «М».

S_i = (m_i * 347 + 8112) mod 443

S_i → {19 403 19 403 211 93 152 152 285 78 403 403 211 270 152 93 19 78 78 19 211 211 211 211 344 19 403 403 270 211 152 93}.

После вычисления отдельных криптогроафических значений всех элементов функции хеширования сообщения «М» и параметра «r» формируется криптограмма функции хеширования, которая включает в свой состав параметр «r» и криптографические значения элементов функции хеширования S_i.

ЭЦП → S → C_h(M) → {r, S_i} → {26 19 403 19 403 211 93 152 152 285 78 403 403 211 270 152 93 19 78 78 19 211 211 211 211 344 19 403 403 270 211 152 93} → 92Т2Тт|··\mТТтM·|2mm2тттт—2ТТMт·|

После вычисления электронной цифровой подписи сообщение «М» вместе с ЭЦП передается по телекоммуникационным каналам абоненту-получателю (абоненту В).

Действия абонента-получателя (абонента В) по аутентификации принятого электронного сообщения «М» (проверка ЭЦП).

10. Получив ЭЦП передаваемого сообщения «М» и само сообщение «М» абонент-получатель (абонент «В») производит вычисление функции хеширования принятого сообщения «М» → h(M)^в. В рассматриваемом примере при передаче сообщения М → «Криптон» функция хеширования определится как:

h(M)^в → {52 48 52 48 50 42 46 46 40 56 48 48 50 54 46 42 52 56 56 52 50 50 50 50 44 52 48 48 54 50 46 42}.

11. После вычисления функции хеширования h(M)^в принятого сообщения «М» абонент-получатель вычисляет значение параметра «V_i»:

V_i = ( m_i^q-2 ) mod q

Для рассматриваемого примера:

V_i = (m_i^q-2 ) mod q = (m_i⁴⁴¹ ) mod 443

Следовательно, множества значений V_i для множества семантических элементов принятого сообщения «М» → {m₁ m₂ … m_i} определится как:

V_i → {213 120 213 120 381 327 183 183 144 356 120 120 381 402 183 327 213 356 356 213 381 381 381 381 292 213 120 120 402 381 183 327}.

12. На следующем шаге алгоритмизации абонентом «В» производится вычисление параметров «Z₁ⁱ» и « Z₂ⁱ» в соответствии со следующими зависимостями:

Z₁ⁱ = (S_i V_i) mod q

Z₂ⁱ = ((q – r) V_i ) mod q

Для рассматриваемого примера:

Z₁ⁱ = (S_i V_i) mod q → {60 73 60 73 208 287 350 350 284 302 73 73 208 5 350 287 60 302 302 60 208 208 208 208 330 60 73 73 5 208 350 287}.

Z₂ⁱ = ((q – r) V_i ) mod q → ((443 – 26) V_i ) mod 443 → (417 V_i ) mod 443 → {221 424 221 424 283 358 115 115 243 47 424 424 283 180 115 358 221 47 47 221 283 283 283 283 382 221 424 424 180 283 115 358}.

13. После вычисления параметров «Z₁ⁱ» и « Z₂ⁱ» с помощью открытого ключа абонента-отправителя (абонента «А») - К_ОА сообщения «М» производится вычисление параметра «U_i» :

U_i = (( * ) mod P) mod q

Для численных значений рассматриваемого примера а = 16 (пункт 2); К_ОА = 482 (пункт 4); Р = 887 и q = 443 (пункт 1) множества значений параметра U_i определятся как:

U_i = (( * ) mod P) mod q = (( * ) mod 887) mod 443 → {26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26 26}.

14. Производится сравнение вычисленных значений U_i с числовым значением параметра «r», принятого в составе электронной цифровой подписи от абонента-отправителя и в случае их полного поэлементного совпадения сообщение «М» признается достоверным (Рис.10) , в противном случае сообщение «М» признается модифицированным (Рис.11).

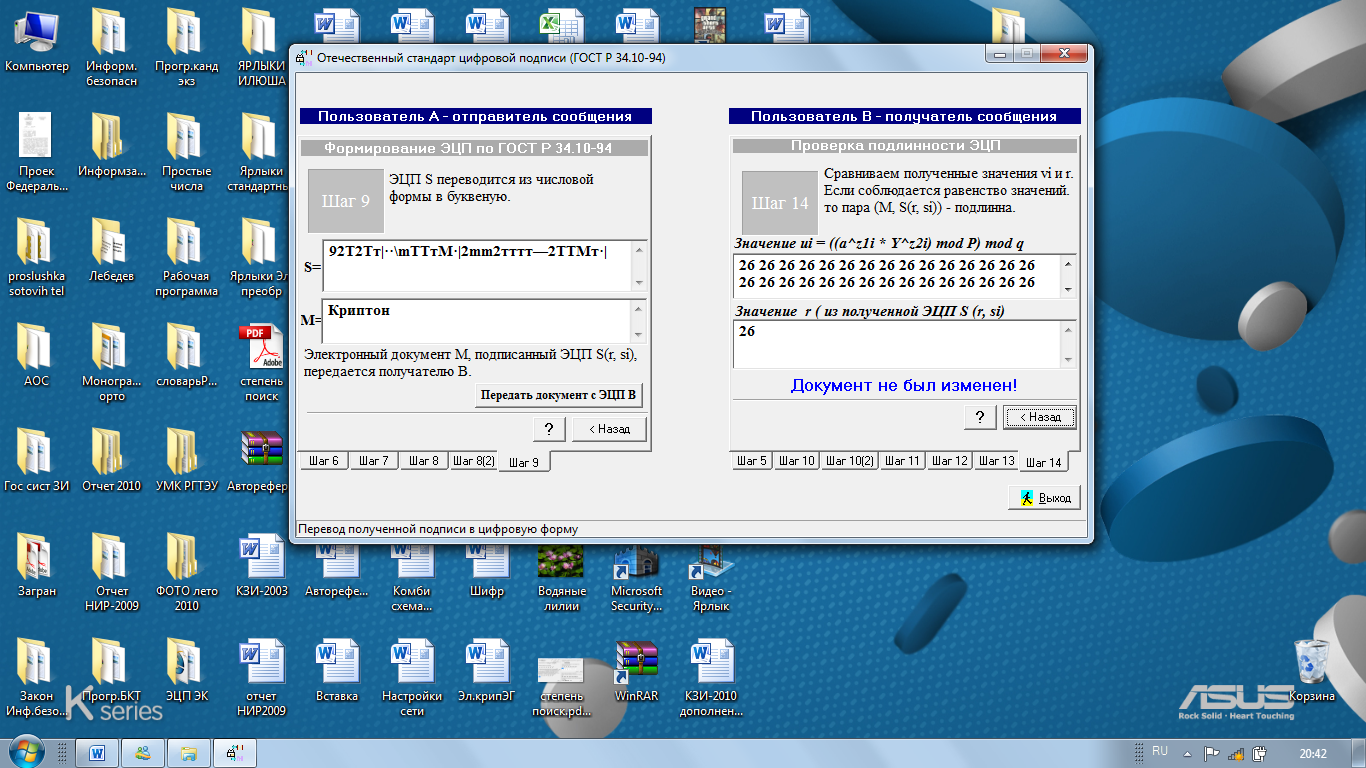
Рис. 10. Аутентификация достоверного сообщения «Криптон».

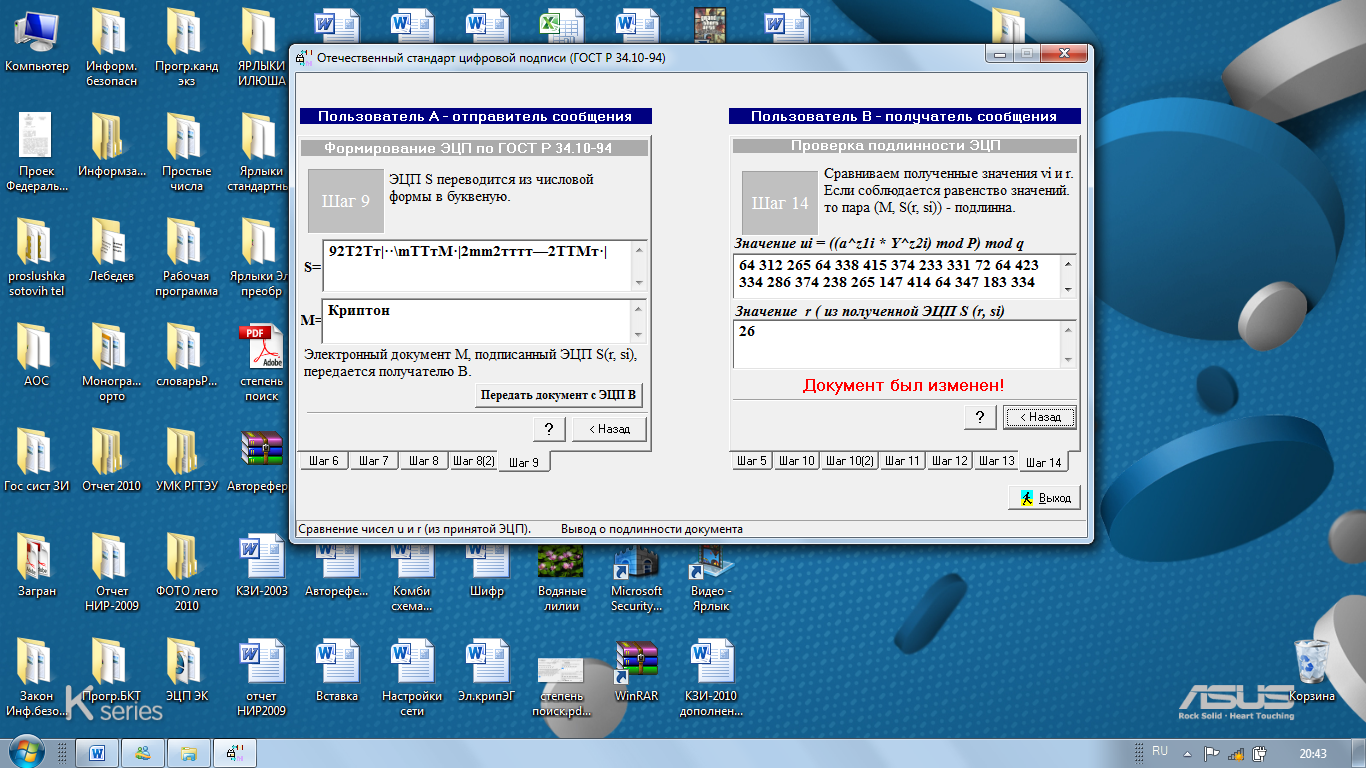
Рис.11. Выявление факта модификации электронного сообщения «Криптон».