4.1. Алгоритм электронной цифровой подписи rsa (Райвест-Шамир-Адлеман).

Впервые в мировой практике аутентификации электронных сообщений на основе формирования и подтверждения подлинности электронной цифровой подписи в 1977 году в Массачусетском технологическом институте США тремя учеными в области криптографических преобразований была разработана математическая модель и реализована криптографическая система аутентификации электронных сообщений RSA.

Этот алгоритм основан на методе факторизации больших целых чисел (разложении большого целого числа на простые множители).

Действия абонента «А» по формированию ЭЦП.

1. Отправитель электронного сообщения на своем компьютере случайным образом генерирует два больших простых числа (размерность простых чисел составляет порядка 100 десятичных знака), затем находит их произведение, которое определяется как модуль криптографических преобразований N = P * Q.

2. После вычисления модуля криптографических преобразований системы RSA производится вычисление функции Эйлера φ(N)

φ(N) = (P-1) * (Q-1).

Числовое значение функции Эйлера определяет, сколько в данном модуле N есть чисел взаимно простых с N:

НОД ( {n_i}; N} = 1,

где: НОД – наибольший общий делитель;

{n_i} – множество чисел взаимно простых с N в диапазоне от 1

до N;

N – модуль системы преобразований.

Детерминированное множество {n_i} чисел взаимно простых с N необходимо для выбора случайным образом из этого множества значения открытого ключа абонента-отправителя исходного сообщения «М», ключа К_ОА при следующих условиях ограничения 1 < К_ОА ≤ φ(N) и НОД (К_ОА; φ(N)) = 1, т.е. числа открытого ключа и значения функции Эйлера должны быть взаимно простыми.

3. На следующем шаге алгоритма RSA производится вычисление закрытого (секретного) ключа абонента-отправителя К_ЗА по следующей формуле:

К_ЗА = К_ОА^-1 mod φ(N)

Вычисление обратного значения К_ОА по заданному модулю при условии, что известна функция Эйлера, несколько упрощается и представленная зависимость преобразуется к виду:

К_ЗА = К_ОА^-1 mod φ(N) = К_ОА^{φ(N) – 1} mod φ(N).

4. В результате выполненных операций вычислены открытые и закрытые параметры системы криптографической аутентификации алгоритма RSA:

- закрытыми секретными параметрами являются К_ЗА – закрытый (секретный) ключ абонента-отправителя сообщения; простые числа P и Q, образующие модуль системы преобразования;

- открытыми параметрами являются К_ОА – открытый ключ абонента-отправителя сообщения «М» и значение модуля N.

5. Открытые параметры системы аутентификации электронных сообщений по каналам теледоступа передаются абоненту-получателю.

6. После вычисления открытого К_ОА и закрытого К_ЗА ключей электронной цифровой подписи выполняется операция формирования ЭЦП электронного сообщения «М». Для чего вычисляется значение хэш-функции исходного сообщения М → h(M)^B. При вычислении хэш-значения сообщения «М» формируется кодовая комбинация размером 256 бит, что составляет 32 десятичных знака.

7. После получения отображения сообщения «М» в виде картежа десятичных чисел хэш-функции, состоящего из 32 знаков (независимо от размера сообщения «М»), производится шифрование каждого числового элемента в соответствии со следующей зависимостью:

S_i = mod N

8. В результате шифрования каждого элемента хэш-функции закрытым ключом абонента-отправителя исходного сообщения формируется электронная цифровая подпись:

С_h(M) = {S_i} = mod N

Исходный открытый текст сообщения «М» и криптограмма значений функции хеширования (ЭЦП) передаются по открытому каналу абоненту-получателю (абоненту «В»).

9. Абонент-получатель, получив электронное сообщение «М» и его ЭЦП проводит операцию аутентификации.

9.1. Для чего изначально выполняется операция дешифрования криптограммы значений функции хеширования С_h(M) = {S_i} = mod N по следующей зависимости:

m_i = mod N.

9.2. Затем выполняется операция хеширования принятого сообщения «М» и сравнение результатов дешифрования криптограммы хэш-функции С_h(M) → h(M)^D с результатом вычисления значения функции хеширования h(M)^В из принятого сообщения «М».

На основании результатов сравнения получаемых значений функций хеширования принимается решение о достоверности принятого сообщения «М».

Алгоритм аутентификации RSA может быть продемонстрирован на следующем числовом примере с числовыми значениями меньшего размера для полноты и наглядности иллюстрации. Пример разбирается на авторском макете автоматизированной обучающей системы по асимметричным криптографическим преобразованиям.

Пример. Построить систему аутентификации электронных сообщений по алгоритму RSA.

Действия абонента-отправителя (абонента «А»).

1. Случайным образом выбираются два простых числа P и Q, например P = 23, Q = 41. Вычисляется модуль криптографических преобразований N = P * Q =23 * 41 = 943.

2. Вычисляется значение функции Эйлера φ(N)

φ(N) = (P -1) * (Q-1) = 22 * 40 = 880.

На множестве чисел от 1 до 943 существует 880 чисел взаимно простых с N = 943.

3. Случайным образом из множества чисел от 1 до 880

1 < К_ОА < φ(N) выбирается значение открытого ключа К_ОА, например К_ОА=337 при условии, что НОД (К_ОА; φ(N)) = НОД (337; 880) = 1, т.е. значения открытого ключа К_ОА и функции Эйлера φ(N) взаимно просты.

4. Вычисляется значение секретного ключа для формирования криптограммы C_h(M):

К_ЗА = К_ОА^{φ(N) – 1} mod φ(N) = 337⁸⁷⁹ mod 880 = 833 mod 880 → 833.

5. Задается исходное сообщение «М», для примера введен одно слово «Криптон». Вычисляется значение функции хеширования для слова «Криптон»:

h(M)^B = 52 48 52 48 50 42 46 46 40 56 48 48 50 54 46 42 52 56 56 52 50 50 50 50 44 52 48 48 54 50 46 42

6. Производится шифрование числового выражения хэш-функции исходного сообщения «Криптон» с использованием закрытого (секретного) ключа абонента-отправителя.

С_h(M) = {S_i} = mod N = m_i⁸³³ mod 943.

C₁ = m₁⁸³³ mod 943 = 52⁸³³ mod 943 = 233 mod 943→233;

C₂ = m₂⁸³³ mod 943 = 48⁸³³ mod 943 = 358 mod 943→358;

C₃ = m₃⁸³³ mod 943 = 52⁸³³ mod 943 = 233 mod 943→233;

----------------------------------------------------------------------------

C₃₂ = m₃₂⁸³³ mod 943 = 42⁸³³ mod 943 = 452 mod 943→452.

После преобразования цифровых значений в соответствии с таблицей Windows-кодировки получаем семантическое отображение ЭЦП:

ЭЦП (Криптон) → С_h(M) = {S_i} = 233 358 233 358 583 452 759 759 204 842 358 358 583 357 759 452 233 842 842 233 583 583 583 583 700 233 358 358 357 583 759 452 → (Ґ(Ґ¦#vvлЙҐҐ¦¤v#(ЙЙ(¦¦¦¦;(ҐҐ¤¦v#

Таким образом ЭЦП сообщения «Криптон» представляет собой криптограмму С_h(M) = С₁ С₂ С₃ … С₃₂. Исходное сообщение «М» и криптограмма числового значения функции хеширования исходного сообщения передаются абоненту-получателю по каналам телекоммуникаций.

Действия пользователя «В» по аутентификации принятого сообщения «М».

7. Получив сообщение «М» и криптограмму хэш-функции h(M)^B абонент-получатель производит дешифрование криптограммы хэш-функции h(M)^B с использованием открытого ключа К_ОА абонента-отправителя по следующей зависимости

h(M)^D = m_i = mod N = mod N = C_i³³⁷ mod 943

m₁ = C₁³³⁷ mod N = 233³³⁷ mod 943 = 52 mod 943 → 52

m₂ = C₂³³⁷ mod N = 358³³⁷ mod 943 = 50 mod 943 → 48

m₃ = C₃³³⁷ mod N = 233³³⁷ mod 943 = 52 mod 943 → 52

------------------------------------------------------------------------

m₃₂ = C₃₂³³⁷ mod N = 452³³⁷ mod 943 = 48 mod 943 →42

8. Затем абонент-получатель вычисляет значение функции хеширования принятого сообщения «М» → «Криптон»:

h(M)^B = 52 48 52 48 50 42 46 46 40 56 48 48 50 54 46 42 52 56 56 52 50 50 50 50 44 52 48 48 54 50 46 42.

9. Сравнивая значения хэш-функций h(M)^D и h(M)^B

h(M)^D = 52 48 52 48 50 42 46 46 40 56 48 48 50 54 46 42 52 56 56 52 50 50 50 50 44 52 48 48 54 50 46 42

h(M)^B = 52 48 52 48 50 42 46 46 40 56 48 48 50 54 46 42 52 56 56 52 50 50 50 50 44 52 48 48 54 50 46 42

абонент-получатель убеждается в достоверности принятого сообщения «М».

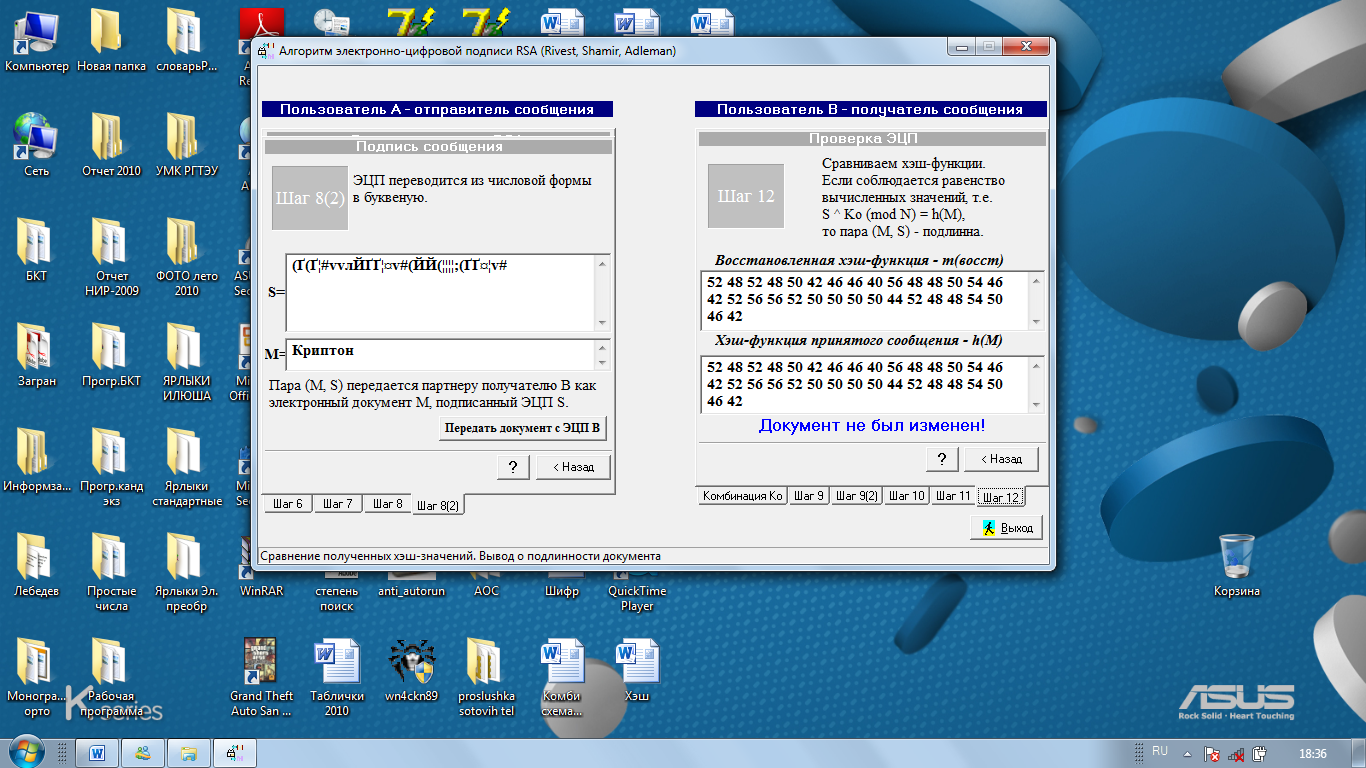
Рис.7. Иллюстрация примера аутентификации сообщения «Криптон».

На рис.7 отображен заключительный фрагмент автоматизированной обучающей системы по аутентификации электронных сообщений в алгоритме RSA.

Для примера модификации принимаемого сообщения вводится изменение в исходное сообщение М → Криптон. Допустим, произведена модификация подписанного сообщения М → Краптон. Результат такой модификации отображен на рис. 8. Система аутентификации зафиксировало это изменение и выдало сообщение, что принятый документ был изменен.

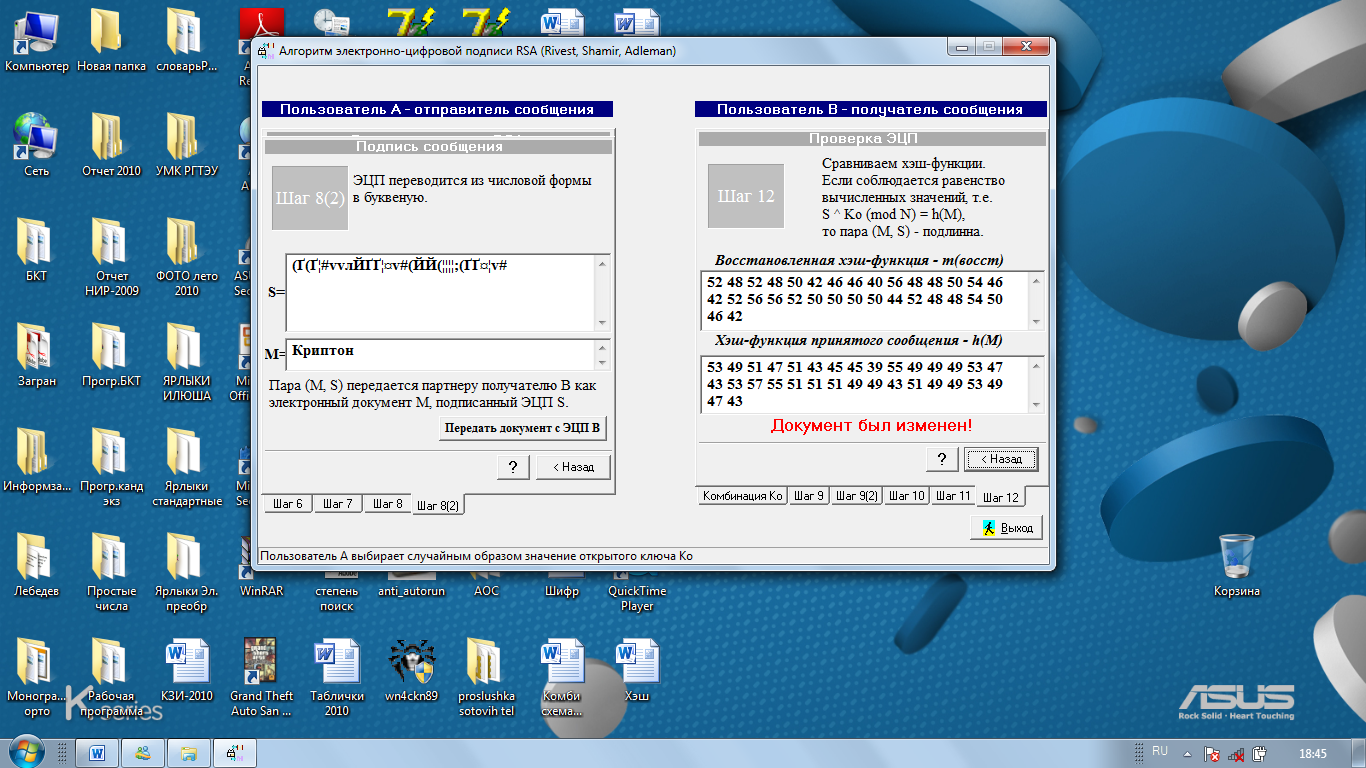
Рис. 8. Фрагмент модификации принимаемого сообщения «М».