7. Дешифрование абонентом а криптограммы, полученной от абонента в с использованием парного секретного симметричного ключа, сформированного по методу Диффи-Хеллмана в метрике эллиптических кривых.

Со стороны абонента А вычисление парного ключа определяется как:

К_АВ = [К_ЗА]К_ОВ mod P

где:

К_АВ – парный секретный симметричный ключ шифрования-дешифрования, формируемый на стороне абонента «А»;

К_ЗА – закрытый (секретный) ключ абонента «А» асимметричной криптосистемы; в рассматриваемом примере К_ЗА= 236;

К_ОВ – открытый ключ абонента «В» асимметричной криптосистемы; в рассматриваемом примере К_ОВ= (X_ОВ; Y_ОВ) = (283; 119).

Следовательно, в рассматриваемом примере:

К_АВ = [К_ЗА]К_ОВ mod P= [236] К_ОВ mod P = [236] (X_ОВ; Y_ОВ) =[236] (283; 119)

Для определения парного секретного симметричного ключа шифрования-дешифрования на стороне абонента «А» операция такого вычисления определяется следующим образом:

- изначально вычисляются операции удвоения точки К_ОВ и всех последующих вычисляемых точек вплоть до [128] К_ОВ (для рассматриваемого примера) поскольку число 128 является максимальным степенного значения 2ⁿ в составе К_ЗА = 236.

- затем вычисляется композиция всего полученного детерминированного множества.

7.1. Вычисление удвоений множества точек заданной эллиптической кривой на стороне абонента «а» по значению точки ков, характеризующей открытый ключ абонента «в».

7.1.1. Вычисление значения удвоения точки ков – [2]ков:

- вычисление углового коэффициента касательной в точке

К_ОВ (X₁; Y₁) = К_ОВ(283; 119)

K = mod P = mod 293 = 53mod 293 → 53.

- вычисление координат точки [2] К_ОВ = (X₂; Y₂)

X₂ = (K² – 2X₁) mod P = (53² - 2*283) mod 293 = 192 mod 293 → 192;

Y₂ = (K*(X₁ – X₂) – Y₁) mod P = (53*(283 – 192) – 119) mod 293 =

= 16 mod 293 → 16.

Следовательно, [2] К_ОВ = (X₂; Y₂) = (192; 16), координаты точки [2] К_ОВ определены как X₂ = 192; Y₂ = 16.

7.1.2. Вычисление точки [4]К_ОВ , как результат удвоения точки [2]К_ОВ ( [2]К_ОВ = (X₂; Y₂) = (192; 16)):

- вычисление углового коэффициента касательной в точке [2]К_ОВ = (X₂; Y₂) = (192; 16)

K = mod P = mod 293 = 160 mod 293 → 160.

- вычисление координат точки [4] К_ОВ = (X₄; Y₄)

X₄ = (K² – 2X₂) mod P = (160² - 2*192) mod 293 = 18 mod 293 → 18;

Y₄ = (K*(X₂ – X₄) – Y₂) mod P = (160*(192 – 18) – 16) mod 293 =

= 282 mod 293 → 282.

Следовательно, [4] К_ОВ = (X₄; Y₄) = (18; 282), координаты точки

[4] К_ОВ определены как X₄ = 18; Y₄ = 282.

7.1.3. Вычисление точки [8]К_ОВ , как результат удвоения точки [4]К_ОВ ( [4]К_ОВ = (X₄; Y₄) = (18; 282)):

- вычисление углового коэффициента касательной в точке [4]К_ОВ = (X₄; Y₄) = (18; 282)

K = 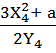mod P = mod 293 = 62 mod 293 → 62.

- вычисление координат точки [8] К_ОВ = (X₈; Y₈)

X₈ = (K² – 2X₄) mod P = (62² - 2*18) mod 293 = 292 mod 293 → 292;

Y₈ = (K*(X₄ – X₈) – Y₄) mod P = (62*(18 – 292) – 282) mod 293 =

= 17 mod 293 → 17.

Следовательно, [8] К_ОВ = (X₈; Y₈) = (292; 17), координаты точки

[8] К_ОВ определены как X₈ = 292; Y₈ = 17.

7.1.4. Вычисление точки [16]К_ОВ , как результат удвоения точки [8]К_ОВ ( [8]К_ОВ = (X₈; Y₈) = (292; 17)):

- вычисление углового коэффициента касательной в точке [8]К_ОВ = (X₈; Y₈) = (292; 17)

K = 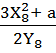mod P = mod 293 = 233 mod 293 → 233.

- вычисление координат точки [16] К_ОВ = (X₁₆; Y₁₆)

X₁₆ = (K² – 2X₈) mod P = (233² - 2*292) mod 293 = 86 mod 293 → 86;

Y₁₆ = (K*(X₈ – X₁₆) – Y₈) mod P = (233*(292 – 86) – 17) mod 293 =

= 222 mod 293 → 222.

Следовательно, [16] К_ОВ = (X₁₆; Y₁₆) = (86; 17), координаты точки

[16] К_ОВ определены как X₁₆ = 86; Y₁₆ = 222.

7.1.5. Вычисление точки [32]К_ОВ , как результат удвоения точки [16]К_ОВ ( [16]К_ОВ = (X₁₆; Y₁₆) = (86; 222)):

- вычисление углового коэффициента касательной в точке [16]К_ОВ = (X₁₆; Y₁₆) = (86; 222)

K = mod P = mod 293 = 277 mod 293 → 277.

- вычисление координат точки [32] К_ОВ = (X₃₂; Y₃₂)

X₃₂ = (K² – 2X₁₆) mod P = (277² - 2*86) mod 293 = 84 mod 293 → 84;

Y₃₂ = (K*(X₁₆ – X₃₂) – Y₁₆) mod P = (277*(86 – 84) – 222) mod 293 =

= 39 mod 293 → 39.

Следовательно, [32] К_ОВ = (X₃₂; Y₃₂) = (84; 39), координаты точки

[32] К_ОВ определены как X₃₂ = 84; Y₃₂ = 39.

7.1.6. Вычисление точки [64]К_ОВ , как результат удвоения точки [32]К_ОВ ( [32]К_ОВ = (X₃₂; Y₃₂) = (84; 39)):

- вычисление углового коэффициента касательной в точке [32]К_ОВ = (X₃₂; Y₃₂) = (84; 39)

K = mod P = mod 293 = 279 mod 293 → 279.

- вычисление координат точки [64] К_ОВ = (X₆₄; Y₆₄)

X₆₄ = (K² – 2X₃₂) mod P = (279² - 2*84) mod 293 = 28 mod 293 → 28;

Y₆₄ = (K*(X₃₂ – X₆₄) – Y₃₂) mod P = (279*(84 – 28) – 39) mod 293 =

= 56 mod 293 → 56.

Следовательно, [64] К_ОВ = (X₆₄; Y₆₄) = (28; 56), координаты точки

[64] К_ОВ определены как X₆₄ = 28; Y₆₄ = 56.

7.1.7. Вычисление точки [128]К_ОВ , как результат удвоения точки [64]К_ОВ ( [64]К_ОВ = (X₆₄; Y₆₄) = (28; 56)):

- вычисление углового коэффициента касательной в точке [64]К_ОВ = (X₆₄; Y₆₄) = (28; 56)

K = mod P = mod 293 = 42 mod 293 → 42.

- вычисление координат точки [128] К_ОВ = (X₁₂₈; Y₁₂₈)

X₁₂₈ = (K² – 2X₆₄) mod P = (42² - 2*28) mod 293 = 243 mod 293 → 243;

Y₁₂₈ = (K*(X₆₄ – X₁₂₈) – Y₆₄) mod P = (42*(28 – 243) – 56) mod 293 =

= 290 mod 293 → 290.

Следовательно, [128] К_ОВ = (X₁₂₈; Y₁₂₈) = (243; 290), координаты точки [128] К_ОВ определены как X₁₂₈ = 243; Y₁₂₈ = 290.