4.1.3. Вычисление координат точки [8]g, как результат удвоения точки [4]g:

- вычисление углового коэффициента касательной в точке [4]G = (X₄; Y₄) = (86; 71)

K = 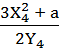mod P = mod 293 = mod 293 = 22196 * 142^-1 mod 293 = 22196 * 142²⁹¹ mod 293 = 22196 * 130 mod 293 = 221 * 130 mod 293 = 28730 mod 293 = 16 mod 293 → 16.

- вычисление координат точки [8]G = (X₈; Y₈)

X₈ = (K² – 2X₄) mod P = (16² - 2*86) mod 293 = 84 mod 293 → 84;

Y₈ = (K*(X₄ – X₈) – Y₄) mod P = (16*(86 – 84) – 71) mod 293 =

= 254 mod 293 → 254.

Следовательно, [8]G = (X₈; Y₈) = (84; 254), координаты точки [8]G определены как X₈ = 84; Y₈ = 254.

4.1.4. Вычисление координат точки [16]g , как результат удвоения точки [8]g:

- вычисление углового коэффициента касательной в точке [8]G = (X₈; Y₈) = (84; 254)

K = 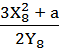mod P = mod 293 = mod 293 = 21176 * 508^-1 = 21176 * 508²⁹¹ mod 293 = 80 * 154 mod 293 = 12320 mod 293 =

= 14 mod 293 → 14.

- вычисление координат точки [16]G = (X₁₆; Y₁₆)

X₁₆ = (K² – 2X₈) mod P = (14² - 2*84) mod 293 = (196 – 168) mod 293 =

= 28 mod 293 → 28;

Y₁₆ = (K*(X₈ – X₁₆) – Y₈) mod P = (14*(84 – 28) – 254) mod 293 = (784 – 254) mod 293 = 530 mod 293 = 237 mod 293 → 237.

Следовательно, [16]G = (X₁₆; Y₁₆) = (28; 237), координаты точки [16]G определены как X₁₆ = 28; Y₁₆ = 237.

4.1.5. Вычисление координат точки [32]g , как результат удвоения точки [16]g:

- вычисление углового коэффициента касательной в точке [16]G = (X₁₆; Y₁₆) = (28; 237)

K = 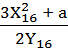mod P = mod 293 = mod 293 = 2360 * 474^-1 mod 293 = 2360 * 474²⁹¹ mod 293 = 16 * 34 mod 293 = 544 mod 293 =

= 251mod 293 → 251.

- вычисление координат точки [32]G = (X₃₂; Y₃₂)

X₃₂ = (K² – 2X₁₆) mod P = (251² - 2*28) mod 293 = (63001 – 56) mod 293 = = 62945 mod 293 = 243 mod 293 → 243;

Y₃₂ = (K*(X₁₆ – X₃₂) – Y₁₆) mod P = (251*(28 – 243) – 237) mod 293 = - 54202 mod 293 = - 290 mod 293 = ( 293 – 290) mod 293 = 3 mod 293 → 3.

Следовательно, [32]G = (X₃₂; Y₃₂) = (243; 3), координаты точки [32]G определены как X₃₂ = 243; Y₃₂= 3.

4.1.6. Вычисление координат точки [64]g , как результат удвоения точки [32]g:

- вычисление углового коэффициента касательной в точке [32]G = (X₃₂; Y₃₂) = (243; 3)

K = 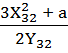mod P = mod 293 = 177155 * 6^-1 mod 293 =

= 177155 * 6²⁹¹ mod 293 = 183 * 49 mod 293 = 8967 mod 293 = 177 mod 293 → 177.

- вычисление координат точки [64]G = (X₆₄; Y₆₄)

X₆₄ = (K² – 2X₃₂) mod P = (177² - 2*243) mod 293 = 30843 mod 293 = 78 mod 293 → 78;

Y₆₄ = (K*(X₃₂ – X₆₄) – Y₃₂) mod P = (177*(243 – 78) – 3) mod 293 = 29202 mod 293 = 195 mod 293 → 195.

Следовательно, [64]G = (X₆₄; Y₆₄) = (78; 195), координаты точки [64]G определены как X₆₄ = 78; Y₆₄ = 195.

4.1.7. Вычисление координат точки [128]g , как результат удвоения точки [64]g:

- вычисление углового коэффициента касательной в точке [64]G = (X₆₄; Y₆₄) = (78; 195)

K = 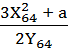mod P = mod 293 = mod 293 = 18260 * 390²⁹¹ = 94 * 145 mod 293 = 13630 mod 293 = 152 mod 293 → 152.

- вычисление координат точки [128]G = (X₁₂₈; Y₁₂₈)

X₁₂₈ = (K² – 2X₆₄) mod P = (152² - 2*78) mod 293 = 22948 mod 293 = 94 mod 293 → 94;

Y₁₂₈ = (K*(X₆₄ – X₁₂₈) – Y₆₄) mod P = (152*(78 – 94) – 195) mod 293 =

= 10 mod 293 → 10.

Следовательно, [128]G = (X₁₂₈; Y₁₂₈) = (94; 10), координаты точки [128]G определены как X₁₂₈ = 94; Y₁₂₈ = 10.