5.Суть принципа суперпозиции и расчета круга методом суперпозиции

Метод наложения.

В основе метода наложения лежит принцип суперпозиции, заключающийся в том, что ток в любой ветви электрической цепи можно рассчитать как алгебраическую сумму токов, вызываемых в ней от каждого источника в отдельности. Ток от отдельно взятого источника называется частным. При расчете частного тока все остальные источники ЭДС заменяются короткозамкнутыми перемычками, а ветви с источниками тока размыкаются. Поскольку в этом случае в рассматриваемых цепях остается только по одному источнику, расчеты производят не решением системы уравнений, а последовательным упрощением цепей путем использования правил для последовательного и параллельного соединения элементов, преобразования звезды в треугольник или треугольника в эквивалентную звезду и т. д.

Напомним основные правила и закономерности эквивалентного преобразования схем.

1. Эквивалентное сопротивление цепи, состоящей из последовательно соединенных сопротивлений, равно сумме этих сопротивлений. Падения напряжений на этих сопротивлениях прямо пропорционально этим сопротивлениям.

2. Эквивалентная проводимость цепи, состоящей из параллельно соединенных сопротивлений, равна сумме проводимостей этих сопротивлений. Протекающие через сопротивления токи прямо пропорциональны их проводимостям или обратно пропорциональны их сопротивлениям.

3. Звезду сопротивлений можно преобразовать в эквивалентный треугольник сопротивлений, как это показано на рис. 4, и наоборот.

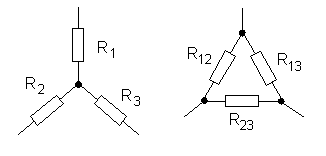
Рис. 4 Эквивалентные звезда и треугольник сопротивлений.

Формулы преобразования звезды сопротивлений в эквивалентный треугольник сопротивлений имеют вид:

  (8)

Для обратного преобразования можно использовать следующие выражения:

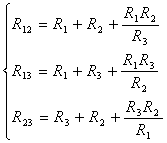  (9)

Метод наложения (МН) основан на применении принципа суперпозиции (наложения).

принцип наложения. Реакция цепи на сумму воздействий равна алгебраической сумме реакций на каждое из воздействий в отдельности.

Под реакцией цепи понимается ток, а под воздействием — действие источников ЭДС или тока. Таким образом, ток в каждой ветви схемы, возникающий под действием всех источников, можно представить как алгебраическую сумму частичных токов этой ветви, вызванных действием каждого источника в отдельности.

Метод наложения предполагает:

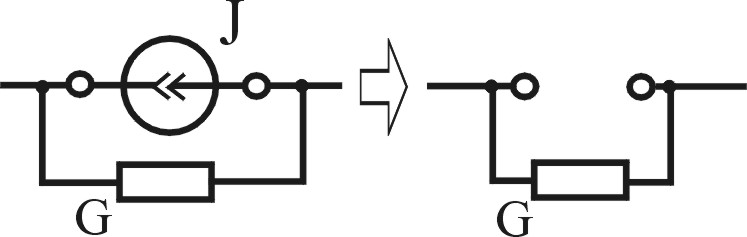
1. Определение количества источников в цепи и составление расчетных схем. При расчете цепей по МН нужно сначала составить расчетные схемы, количество которых равно количеству источников в цепи. В каждой из расчетных схем остается только один из источников, а остальные источники «устраняются» таким образом, что вместо реальных источников в схеме остаются их внутренние сопротивления, идеальный источник ЭДС заменяется перемычкой, а идеальный источник тока — разрывом (табл.2.1).При наличии в цепи более трех источников расчеты усложняются, поэтому применение этого метода становится нерациональным.

Таблица 2.1 — Замена источников при составлении частичных схем по МН

Замена по МН	идеальный	реальный
Источник ЭДС
Источник тока