1. Первый и второй законы Кирхгофа

Первый закон Кирхгофа. Алгебраическая сумма токов, сходящихся в узле электрической цепи, равна нулю:

,

где п — количество ветвей, подключенных к узлу.

Токи, направленные к узлу, входят в сумму со знаком «+», от узла — со знаком «-». Этот закон можно сформулировать и следующим образом: сумма токов, входящих в узел, равна сумме токов, выходящих из узла. Это подтверждает физическую закономерность: в узле не должно происходить накопления зарядов.

Применительно к фрагменту цепи, приведенному на рис.2.4, первый закон Кирхгофа запишется так:

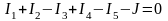либо .

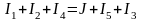Если в ветви есть источник тока, то ток ветви равен току этого источника.

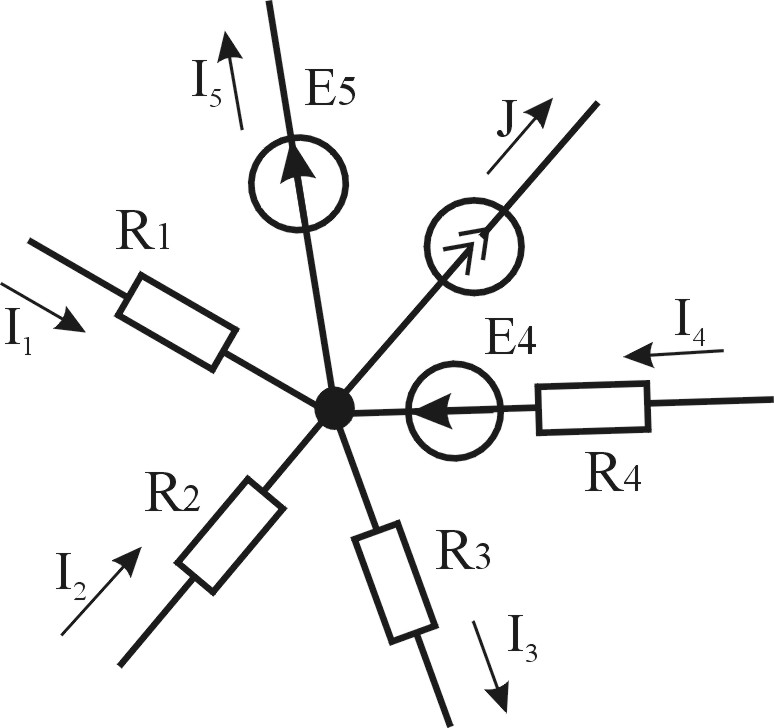
Рисунок 2.4 — Узел электрической цепи

Второй закон Кирхгофа. Алгебраическая сумма напряжений на всех ветвях рассматриваемого контура равна нулю: .

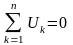Другая формулировка: Алгебраическая сумма падений напряжений на всех сопротивлениях данного контура равна алгебраической сумме ЭДС, действующих в контуре:

2. .

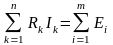Знак падения напряжения и ЭДС сопоставляется с направлением обхода контура. Падение напряжения записываются со знаком «+» при совпадении направления тока в соответствующей ветви с выбранным направлением обхода контура, со знаком «-» при противоположных направлениях. ЭДС принимаются положительными при совпадении их направления с направлением обхода контура.

Запишем уравнение по второму закону Кирхгофа применительно к контуру, приведенному на рис.2.5. В соответствии с выбранным направлением обхода контура токи I₂ и I₃ , а значит, и падения напряжения на сопротивлениях R₂ и R₃ входят в левую часть уравнения со знаком «+» ; падения напряжения на сопротивлениях R₁ и R₄ входят в левую часть уравнения со знаком «-».

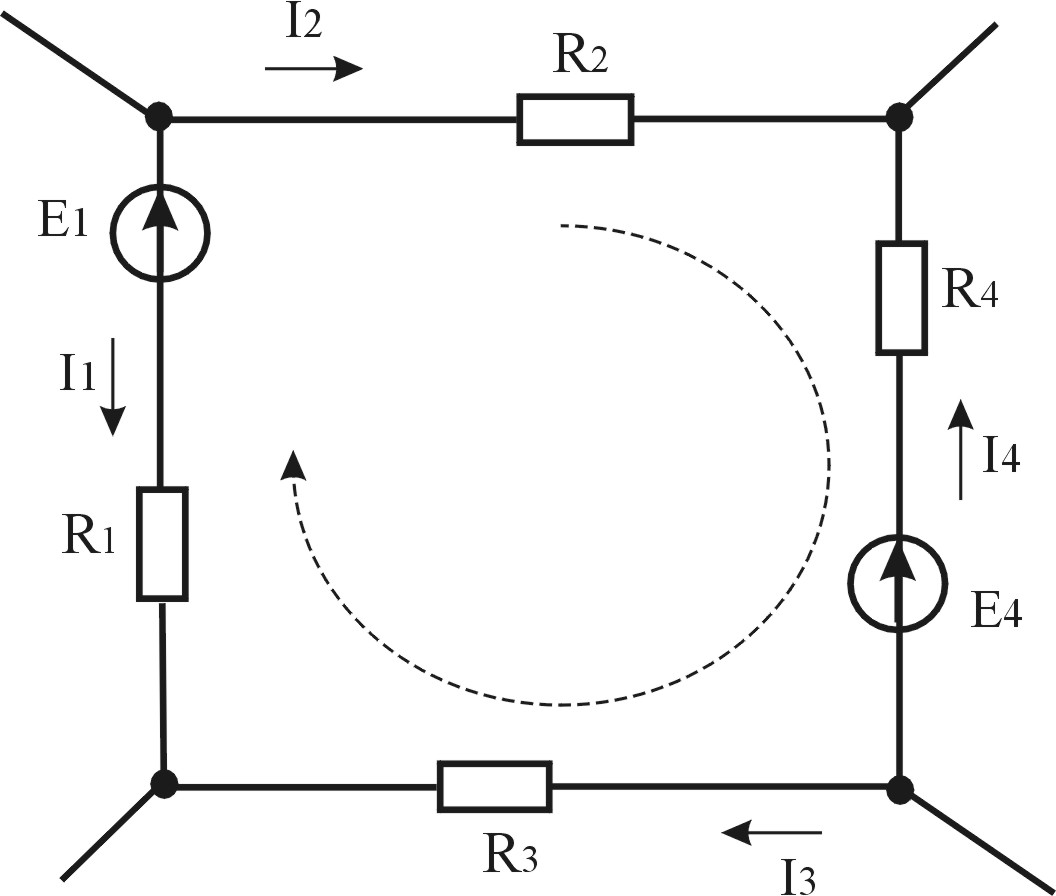
Рисунок 2.5 — Контур электрической цепи

В правую часть запишем алгебраическую сумму ЭДС. Направление ЭДС Е₁ и обхода контура совпадают (знак ЭДС «+»), а ЭДС Е₂ — противоположно обходу (знак ЭДС «+») :

.

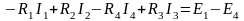Если хотя бы в одну ветвь контура входит идеальный источник тока, то уравнение по второму закону Кирхгофа не может быть составлено, т.к. источник тока имеет бесконечно большое сопротивление (разрыв в контуре).

2 Схема электрической цепи, ее топологические элементы

Топологические параметры цепи

Электрической цепью называют совокупность тел и сред, образующих замкнутые пути для протекания электрического тока. Обычно физические объекты и среду, в которой протекает электрический ток, упрощают до условных элементов и связей между ними. Тогда определение цепи можно сформулировать как совокупность различных элементов, объединенных друг с другом соединениями или связями, по которым может протекать электрический ток. Элементами электрической цепи являются источники электрической энергии, активные и реактивные сопротивления (см. и изучите условные обозначения для электрических схем). Связи в электрической цепи изображаются линиями и по смыслу соответствуют идеальным проводникам с нулевым сопротивлением.

Связи цепи, наряду с элементами, определяют ее свойства и для одних и тех же элементов можно создать множество различных электрических цепей различающихся только связями.

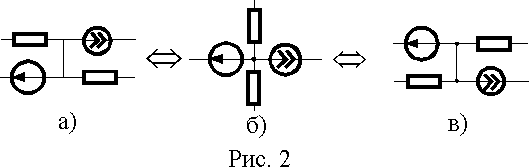
Связи элементов электрической цепи обладают топологическими свойствами, т.е. они не изменяются при любых преобразованиях, производимых без разрыва связей. Пример такого преобразования показан на рис. 1.

 

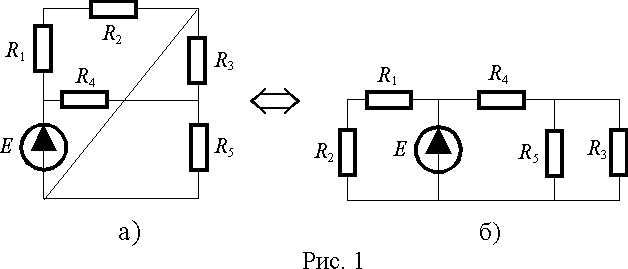
Возможность взаимно однозначного преобразования электрической цепи позволяет использовать его до начала анализа для приведения схемы к наиболее простому и легко воспринимаемому виду. Так схема на рис. 1 б) выглядит значительно проще, чем схема а).

 

Для описания топологических свойств электрической цепи используются топологические понятия, основными из которых являются узел, ветвь и контур.

Узлом электрической цепи называют место (точку) соединения трех и более элементов.

Графически такое соединение может изображаться различными способами.

Обратите внимание на точку в месте пересечения линий схемы. Если она отсутствует, то это означает отсутствие соединения. Точка может не ставиться там, где при пересечении линия заканчивается (рисунок а)).

Узел не обязательно имеет вид точки. На рис. 1 б) вся нижняя линия связи, соединяющая R₂, E, R₅ и R₃ , является узлом, а на рис. 1 а) этот же узел представлен диагональной связью.