Вопрос 17.

Правило трёх сигм

При рассм нормального закона распределения выделяется важный частный случай, известный как правило трех сигм. Запишем в-ть т\ч отклонение нормально распр сл\в от мат\ожидания меньше заданной величины D:

  Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

Т.е. в-ть т\ ч сл\в отклонится от своего мат\о на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю. Это правило называется правилом трех сигм.На практике считается, что если для какой – либо сл\в выполняется правило трех сигм, то эта сл\в имеет нормальное распределение.

Пример. Нормально распределенная сл\в Х задана своими параметрами – а =2 – мат\о и s = 1 – среднее квадратическое отклонение. Требуется написать плотность вер-ти и построить ее график, найти в-ть того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2. Плотность распределения имеет вид:

П остроим график:

Найдем в-ть попадания случайной величины в интервал (1; 3).

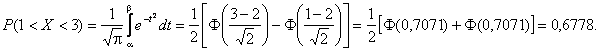
Найдем в-ть отклонения сл\в от мат\о на величину, не большую чем 2.

Тот же результат может быть получен с использованием нормированной функции Лапласа.

Вопрос 18.

Биномиальным наз-ся распределение сл\в, в кот она принимает последовательность целых неотрицательных значений с вер-ми определяемыми по формуле Бернулли.

мат\о и дисперсия биномиально распределённой сл\величины.

Законом распределения Пуассона наз распр-е сл\в, в кот она принимает последовательность целых неотрицательных значений с вер-ми определ-ся по формуле Пуассона. Если имеет место распределение Пуассона заданного распр-я , то мат\о находится

Распределение Пуассона. Пусть производится n независимых испытаний, в кот появление соб А имеет в-ть р. Если число испытаний n достаточно велико, а в-ть появления соб А в каждом испытании мало, то для нахождения в-ти появления события А k раз находится след образом: Произведение np сохраняет постоянное значение: , это означает, что среднее число появления соб в различных сериях испытаний (при разном n) остается неизменным.

По формуле Бернулли получаем:

;

 Найдем предел этой вероятности при n  ∞.

Получаем формулу распределения Пуассона:

Вопрос 19.

Непрерывную случайную величину нельзя охарактеризовать перечнем всех возможных ее значений и их вероятностей. Естественно, встает вопрос о том, нельзя ли охарактеризовать случайную величину иным способом, одинаково годным как для дискретных, так и для непрерывных случайных величин.      Функцией распределения случайной величины Х называют функцию F(x), определяющую для каждого значения х, вероятность того, что случайная величина Х примет значение меньше х, т.е.      F(x) = P (X <x).      Иногда функцию F(x) называют интегральной функцией распределения.      Функция распределения обладает следующими свойствами:      1. Значение функции распределения принадлежит отрезку [0,1]: 0 ≤ F(x) ≤ 1.      2. Функции распределения есть неубывающая функция.      3. Вероятность того, что случайная величина Х примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:       Р(а < X < b) = F(b) – F(а).                                          (2.1)      4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то       F(x) = 0 при х ≤ а ;F(x) = 1 при х ≥ b.      5.      Справедливы следующие предельные отношения:       .      Для дискретной случайной величины Х, которая может принимать значения х₁, х₂, …,х_n, функция распределения имеет вид            где неравенство под знаком суммы означает, что суммирование касается всех тех значений х_i, величина которых меньше х.

20. Распределение хи-квадрат Пирсона, Стьюдента, Фишера.

Распределением хи-квадрат с k степенями свободы называется распределение суммы квадратов k независимых случайных величин, распределенных по стандартному нормальному закону, т.е.

Где ( i= 1,2,….k) имеет нормальное распределение N(0;1).

При этом число слагаемых, т.е. i , называется «числом степеней свободы» распределения хи – квадрат.

Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных.

Распределение t Стьюдента – это распределение случайной величины

где случайные величины U и X независимы, U имеет распределение стандартное нормальное распределение N(0,1), а X – распределение хи – квадрат с n степенями свободы. При этом n называется «числом степеней свободы» распределения Стьюдента.

Распределение Стьюдента было введено в 1908 г. английским статистиком В. Госсетом, работавшем на фабрике, выпускающей пиво. Вероятностно-статистические методы использовались для принятия экономических и технических решений на этой фабрике, поэтому ее руководство запрещало В. Госсету публиковать научные статьи под своим именем.

В настоящее время распределение Стьюдента – одно из наиболее известных распределений среди используемых при анализе реальных данных. Его применяют при оценивании математического ожидания, прогнозного значения и других характеристик с помощью доверительных интервалов, по проверке гипотез о значениях математических ожиданий, коэффициентов регрессионной зависимости, гипотез однородности выборок и т.д.

Распределение Фишера – это распределение случайной величины

где случайные величины Х1 и Х2 независимы и имеют распределения хи – квадрат с числом степеней свободы k1 и k2 соответственно. При этом пара (k1, k2) – пара «чисел степеней свободы» распределения Фишера, а именно, k1 – число степеней свободы числителя, а k2 – число степеней свободы знаменателя. Распределение случайной величины F названо в честь великого английского статистика Р.Фишера (1890-1962), активно использовавшего его в своих работах.

Распределение Фишера используют при проверке гипотез об адекватности модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики.

21. Понятие и способы задания многомерных СВ.

Многомерной (n-мерной) случайной величиной называется где Случайные величины называются компонентами

Например, положение центра тяжести самолета — трехмерная случайная величина

Рассмотрим дискретные и непрерывные двумерные СВ. Закон распределения дискретной двумерной СВ может быть задан в виде таблицы распределения вероятностей:

η ξ			….
			….
			….
….	….	….	….	….
			….

причем

Закон распределения дискретной и непрерывной СВ можно задать в виде функции распределения.

Обозначим вероятность того, что удовлетворяет неравенствам через

Функцией распределения вероятностей СВ называется Для непрерывной СВ вводится понятие плотности распределения вероятностей.

22. Числовые характеристики многомерных СВ.

Функцией распределения вероятностей СВ называется Для непрерывной СВ вводится понятие плотности распределения вероятностей.

Плотностью распределения вероятностей СВ с функцией распределения F(x,y) называется непрерывная в функция такая, что

Аналогично случаю одномерной СВ имеем формулы для вычисления вероятности того, что значения двумерной СВ с плотностью распределения окажутся в области

и функции распределения СВ :

причем

Математическое ожидание двумерной СВ :

где

Точка называется центром рассеивания двумерной СВ.

Дисперсия где определяются по формуле.

Рассмотрим нормальный закон распределения на плоскости.

Распределение непрерывной двумерной СВ называется нормальным, если плотность распределения выражается формулой

Точка 0(0,0) — центр рассеивания СВ — главные средние квадратические отклонения.

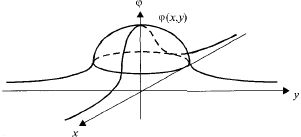
График плотности

23. Сущность закона больших чисел. Неравенство Чебышева.

Теоремы закона больших чисел устанавливают зависимость между случайностью и необходимостью.

Закон больших чисел- это обобщенное название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным.

Неравенство Чебышева.

Лемма: Если случайная величина Х имеет конечные математическое ожидание М(Х) и дисперсию Д(Х), то для любого положительного e справедливо неравенство

.

Данное неравенство часто дает грубую, не представляющую интереса оценку.

Тем не менее данное неравенство имеет большое теоретическое значение. С его помощью доказываются теоремы и делаются теоретические выводы.

24. Теорема Чебышева и ее следствия.

Теорема Чебышева: При достаточно большом числе независимых случайных величин Х1, Х2, Х3, ..., Хn, дисперсия каждой из которых не превышает одного и того же постоянного числа В, для произвольного сколько угодно малого числа e справедливо неравенство

P

Из теоремы следует, что среднее арифметическое случайных величин при возрастании их числа проявляет свойство устойчивости, т. е. стремится по вероятности к неслучайной величине, которой является среднее арифметическое математических ожиданий этих величин, т.е. вероятность отклонения по абсолютной величине среднего арифметического случайных величин от среднего арифметического их математических ожиданий меньше чем на e при неограниченном возрастании n стремится к 1, т.е. становится практически достоверным событием.

Следствие 1. Если независимые случайные величины имеют одинаковые, равные , математические ожидания, дисперсии их ограничены одной и той же постоянной С, а число их достаточно велико, то, сколько бы мало на было данное положительное число , как угодно близка к единице вероятность того, что отклонение средней арифметической этих случайных величин от не превзойдет по абсолютной величине .

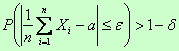Следовательно, по закону больших чисел средняя арифметическая достаточно большого числа измерений практически будет как угодно мало отличаться от истинного значения искомой величины.

Следствие 2. (Теорема Бернулли.)

Если вероятность p наступления события А в каждом из n независимых испытаний постоянна, а их число достаточно велико, то сколь угодно близка к единице вероятность того, что частота появления события как угодно мало отличается от вероятности p его появления:

Теорема Бернулли, утверждает, что если вероятность события одинакова во всех испытаниях, то с увеличением числа испытаний частота события стремится к вероятности события и перестает быть случайной.На практике сравнительно редко встречаются опыты, в которых вероятность появления события в любом опыте неизменна, чаще она разная в разных опытах.

Следствие 3. (Теорема Пуассона.)

Если вероятность появления события A в i-ом испытании не меняется, когда становятся известными результаты предыдущих испытаний, а их число достаточно велико, то сколь угодно близка к единице вероятность того, что частота появления события как угодно мало отличается от средней арифметической вероятностей :

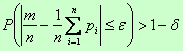
Теорема Пуассона утверждает, что частота события в серии независимых испытаний стремится к среднему арифметическому его вероятностей и перестает быть случайной.

В заключение заметим, что ни одна из рассмотренных теорем не дает ни точного, ни даже приближенного значения искомой вероятности, а указывается лишь нижняя или верхняя граница ее.