Вопрос 11.

Скорость изменения функции распределения хар-ся плотностью распр-я. Обозначается символом . Плотностью вер-ти (плотностью распр-я) НСВ Х наз-ся производная её ф-ии распр-я

Свойства плотности распр-я (ПР):

С1. ПР – неотрицательная функция. ;

С2. Вер-ть попадания НСВ в интервал [a,b] равна определённому интегралу от её плотности вер-ти в пределах от a до b, т.е.

С3. Ф-я распр НСВ м\б выражена через плотность вер-ти по формуле:

С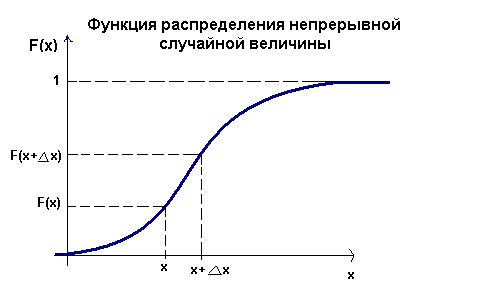 4. Несобственный интеграл в бесконечных пределах от плотности вер-ти НСВ =1. .

Вопрос 12.

Из формулы P{Α ≤ X < Β}=F(Β)-F(Α)следует, что вероятность попадания случайной величины в заданный интервал определяется скоростью изменения функции распределения вероятностей на этом интервале. Скорость изменения непрерывной функции равна ее производной. Это позволяет ввести новую функцию для задания случайной величины. Рассмотрим снова вероятность попадания случайной величины в интервал [x,x+Δx]:

P{x≤X<x+Δx}=F(x+Δx)-F(x).

Пусть Х - непрерывная случайная величина. Тогда для малых значений Δx эта вероятность будет также достаточно малой. Поделим ее на Δx и перейдем к пределу при Δx →0:

lim_{Δx →0}(P{x≤X<x+Δx}/Δx)=lim_{Δx →0}(F(x+Δx)-F(x))/Δx).

Если это предел существует, то он равен производной от функции распределения F(x):

 lim_{Δx →0}(F(x+Δx)-F(x))/Δx)=F'(x)=f(x).

Числовые характеристики отражают те или иные особенности распределения.

1. Математическое ожидание НСВ X определяется по формуле:

  Если НСВ X определена на интервале (a;b), то:  

2. Мода НСВ X будет определяться как максимум ее дифференциаль­ной функции:

3. Медиана определяется как значение случайной величины, которое делит площадь под дифференциальной функцией на две равные части.

4. Дисперсия НСВ   Все свойства дисперсии и математического ожидания, установленные для ДСВ, сохраняются для НСВ.

Вопрос 13.

Непрерывная случайная величина Х имеет равномерное распределение на отрезке [a, b], если ее плотность имеет следующий вид:            График плотности распределения показан на рис. 2.9.                  φ(х)            Рис. 2.9      Найдем значение постоянной С. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то       ,      откуда С = 1/(b – a).      Пусть [ α, β ] Ì [a, b]. Тогда  ,     т.е.       ,                                                                         (2.9)      где L – длина (линейная мера) всего отрезка [a, b] и   – длина частичного отрезка [ α, β].      Значения случайной величины Х, т.е. точки х отрезка [a,b], можно рассматривать как всевозможные элементарные исходы некоторого испытания. Пусть событие А состоит в том, что результат испытания принадлежит отрезку [ α, β] Ì [a, b]. Тогда точки отрезка [ α, β] есть благоприятные элементарные исходы события А.      Согласно формуле (2.9) имеем геометрическое определение вероятности: под вероятностью события А понимается отношение меры   множества элементарных исходов, благоприятствующих событию А, к мере L множества всех возможных элементарных исходов в предположении, что они равновозможны:       .      Это определение естественно переносит классическое определение вероятности на случай бесконечного числа элементарных исходов (случаев).      Аналогичное определение можно ввести также тогда, когда элементарные исходы испытания представляют собой точки плоскости или пространства.

Задача. В течение часа 0 ≤ t ≤ 1 (t – время в часах) на остановку прибывает один и только один автобус. Какова вероятность того, что пассажиру, пришедшему на эту остановку в момент времени t = 0, придется ожидать автобус не более 10 минут?      Решение . Здесь множество всех элементарных исходов образует отрезок [0,1], временная длина которого L =1, а множество благоприятных элементарных исходов составляет отрезок [0,1/6] временной длины  =1/6.      Поэтому искомая вероятность есть        .