Решение систем линейных уравнений методом Гаусса

Пусть имеется система линейных уравнений. Очевидно, что если к одному из уравнений системы прибавить другое, мысленно умноженное на какое-нибудь число, получится система, равносильная данной. Не нарушают равносильности также умножение обеих частей одного из уравнений на число, отличное от нуля, и перестановка уравнений. Этим действиям с уравнениями системы отвечают допустимые действия со строками так называемой расширенной матрицы системы.

Расширенной матрицей системы называется матрица коэффициентов при неизвестных A, к которой присоединён столбец свободных членов B, отделённый от A вертикальной чертой. Расширенная матрица имеет вид .

К преобразованиям, не нарушающим равносильности, можно отнести изменение нумерации неизвестных. Изменению нумерации неизвестных отвечает перестановка столбцов, составленных из коэффициентов при этих неизвестных. Поэтому перестановка столбцов, не затрагивающая столбца свободных членов, также относится к допустимым преобразованиям.

Сначала рассмотрим метод Гаусса на примере системы трёх линейных уравнений с тремя неизвестными в предположении, что главный определитель системы отличен от нуля¹. В этом случае суть метода Гаусса состоит в преобразовании данной системы в систему с треугольной матрицей.

Для системы матрица 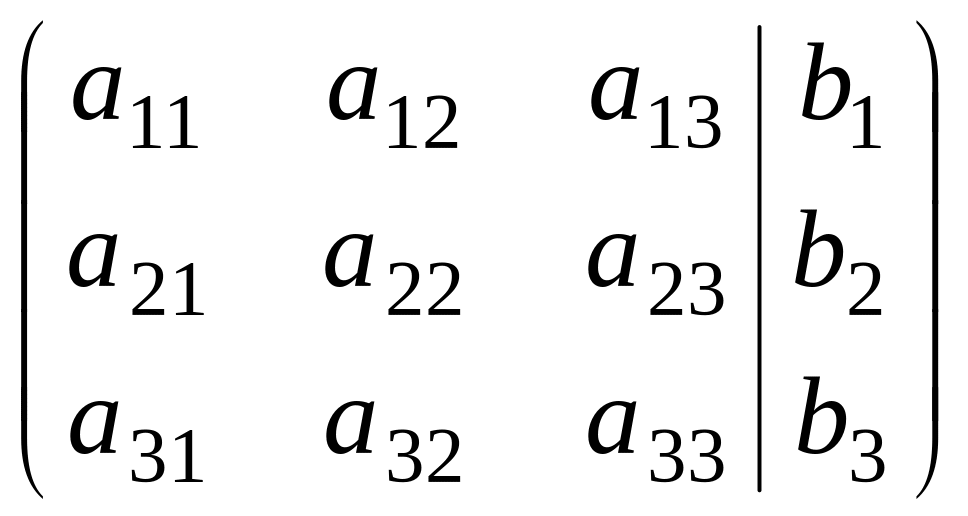является расширенной матрицей.

Схематично метод Гаусса можно изобразить так:

Первый этап Второй этап Третий этап

   .

Преобразования можно продолжить с целью получить систему с единичной матрицей. В этом случае говорят о методе Гаусса-Жордана.

 

Третий этап Четвёртый этап Пятый этап

Пример. Пусть дана система

Выпишем расширенную матрицу и выполним нужные преобразования:    

     .

Последняя матрица соответствует системе . Подставив во второе уравнение , найдём, что . Затем, подставляя в первое уравнение и , найдём, что . Решение системы методом Гаусса завершено.

Метод Гаусса-Жордана отличается от метода Гаусса тем, что вычисление неизвестных производится в матричной форме. Матрица подвергается дальнейшим преобразованиям: прибавляем ко второй и к первой строкам третью, умноженную на –2 и на –3, соответственно. Далее,  ~ , откуда .

E …….. …….. …….. . . . 0 0 k n-k k m m-k n

Рассмотрим теперь метод Гаусса в ситуации, когда либо число уравнений не совпадает с числом неизвестных, либо неизвестно, отличен ли от нуля главный определитель системы. Приведём при помощи допустимых преобразований расположенную до черты часть расширенной матрицы к каноническому или почти каноническому виду. При этом матрица A, превратится в имеющую канонический или почти канонический вид матрицу . Столбец B также изменится и станет столбцом . В результате получается преобразованная расширенная матрица .

исследуем систему с такой расширенной матрицей на совместность.

Если , и хотя бы один элемент столбца , с номером большим k, не равен нулю, пусть это будет элемент ( ), то система несовместна, так как содержит уравнение , не имеющее решений при .

Во всех остальных случаях система совместна. Рассмотрим эти случаи.

E …….. …….. …….. . . . 0 0 0 k n-k k m m-k n

Если , и все элементы столбца с номерами, большими k, равны нулю, последние m-k уравнений можно отбросить, так как все они имеют вид и им удовлетворяют любые числа. Поэтому можно считать, что .

Имеется два варианта: и . При

E …….. …….. …….. . . . k n-k k=m n

матрица оказывается единичной (или треугольной) и тогда система, очевидно, имеет решение, притом единственное.

Пусть . Придавая произвольные значения неизвестным с номерами, большими k (такие неизвестные называются свободными), найдём первые k неизвестных (они называются базисными). В этом случае система, очевидно, имеет бесконечно много решений.

Однородные (с нулевыми правыми частями) системы линейных уравнений всегда совместны, поскольку имеют нулевое (состоящее из нулей) решение. Это решение единственно, если . Если же , множество решений однородной системы бесконечно и, что особенно важно, содержит ненулевые решения.

Отметим, что во всех случаях, когда система совместна, матрица , так же как и , имеет канонический вид.

Пример. Пусть расширенная матрица некоторой системы линейных уравнений при помощи допустимых преобразований приведена к виду . Система, очевидно, совместна. Найдём все её решения. Отбрасывая третью и четвёртую строчки (они состоят из нулей), получим систему . Пусть t, u, v – произвольные числа. Положим свободные неизвестные равными этим числам, то есть будем считать, что . Тогда из первого уравнения следует, что , а из второго, что . Полученные формулы вычисления неизвестных дают бесконечно много решений.

Если в столбце свободных членов третий или четвёртый элемент был бы не 0, а, например, 1, то система была бы несовместной, так как одно из её уравнений имело бы вид: . Такое уравнение, а вместе с ним и система, решений не имеет.