Свойства определителей

1. Определитель, содержащий строку, состоящую из нулей, равен нулю.

2. Определитель, содержащий две одинаковые строки, равен нулю.

3. При перестановке двух строк определитель меняет знак.

4. Если элементы какой-нибудь строки определителя имеют общий множитель, его можно вынести за знак определителя.

5. Определитель, содержащий две пропорциональные строки, равен нулю.

6. Если каждый элемент какой-нибудь строки определителя представлен в виде суммы двух слагаемых, то этот определитель равен сумме двух определителей, в соответствующих строках которых стоят: в одном из них первые слагаемые, в другом – вторые.

7. Определитель не изменится, если к какой-нибудь его строке прибавить другую строку, умноженную на какое-нибудь число.

8. Cумма произведений элементов какой-нибудь его строки на алгебраические дополнения элементов другой строки равна нулю.

аналогичные свойства определителя можно сформулировать для его столбцов.

Для определителей второго порядка все свойства легко доказываются непосредственным вычислением. Для определителей третьего порядка доказательства опираются на теорему о разложении по строкам и столбцам.

докажем свойства 6, 7 и 8 для определителей третьего порядка.

Выпишем шестое свойство:

. Разложив, каждый из определителей по первой строке, и выполнив элементарные преобразования, убедимся в том, что правая часть равна левой.

Свойство 7 состоит в том, что .

определитель, стоящий в правой части, согласно свойству 6, равен сумме . По свойству 5 второе слагаемое равно нулю, так как содержит пропорциональные строки. Остаётся первое слагаемое, равное левой части.

Докажем свойство 8. Сумма произведений элементов третьей строки определителя на алгебраические дополнения элементов первой строки совпадает с суммой, полученной при разложении по первой

строке . Эта сумма, , равна нулю, так как последний определитель (в силу свойства 2) равен нулю. Вместе с ней равен нулю и исходный определитель.

Квадратная матрица называется невырожденной, если её определитель отличен от нуля, в противном случае она называется вырожденной.

Невырожденными, очевидно, являются треугольные и единичные матрицы.

Любая невырожденная матрица имеет обратную. Если = , то обратную матрицу A^–1 можно вычислить по следующей формуле (приводим формулу для квадратной матрицы третьего порядка, для квадратных матриц других порядков формулы аналогичны):

= .

Правильность вычисления матрицы A^–1 проверяется умножением A на A^–1. Выполним эту проверку.

AA^–1 = = .

Поясним, что здесь при вычислении диагональных элементов произведения элементы строк матрицы A умножаются на алгебраические дополнения этих элементов, так что получаются Δ. Когда же вычисляются недиагональные элементы произведения, элементы строки умножаются на «чужие» алгебраические дополнения и, по свойству 8, получаются нули.

Формулы Крамера

Рассмотрим систему трёх линейных уравнений с тремя неизвестными . Определитель Δ = , называется главным определителем системы.

Если матрица коэффициентов системы не вырождена, то есть , то решение системы можно найти по формулам Крамера:

,

где , , .

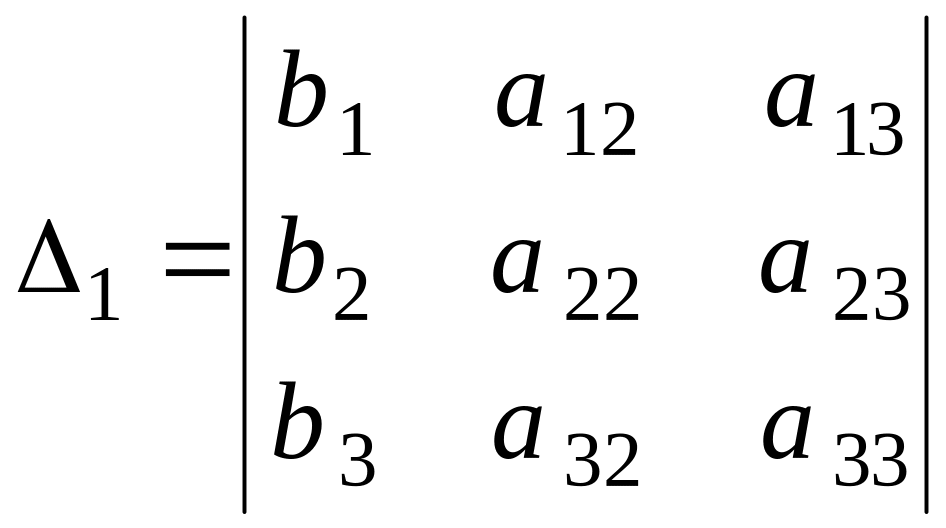Аналогичные формулы (мы принимаем их на веру, без доказательства) справедливы для любой системы линейных уравнений с невырожденной матрицей коэффициентов.

С л е д с т в и е ф о р м у л К р а м е р а. Если главный определительсистемы линейных уравнений отличен от нуля, то система имеет единственное решение.

В частности, если главный определитель системы линейных уравнений, свободные члены которой равны нулю (такая система называется однородной), отличен от нуля, то система имеет единственное нулевое (состоящее из нулей) решение.

Так, однородная система имеет, очевидно, решение . Оно единственно, если .