Умножение матриц

Операция умножения определяется не для всяких двух матриц. две матрицы можно перемножить только в том случае, если число столбцов одной матрицы совпадает с числом строк другой.

О п р е д е л е н и е. Пусть m  k – размерность матрицы А, а k  n – размерность матрицы В. Произведением матрицы А на матрицу В называется матрица С (С = АВ) размерности m  n, элементы c_{i j} которой вычисляются по формуле

,

где – элементы i-й строки матрицы А, а – элементы j-го столбца матрицы В.

Сформулируем правило умножения матриц словесно.

Чтобы вычислить элемент произведения двух матриц, стоящий на пересечении i-й строки и j-го столбца, нужно элементы i-й строки первой матрицы умножить на соответствующие элементы j-го столбца второй матрицы и полученные произведения сложить.

Условная схема умножения матриц такова: (  ). Первая стрелка показывает направление перемещения по строкам первой матрицы, вторая – по столбцам второй.

Отметим, что произведение матриц содержит столько же строк, сколько первая матрица, и столько же столбцов, сколько вторая. В частности, при умножении матрицы-строки на какую-нибудь другую матрицу получается матрица-строка. Если же какая-то матрица умножается на матрицу-столбец, получается матрица-столбец. При умножении матрицы-строки на матрицу-столбец получается матрица размерности 1×1, то есть число.

При умножении квадратных матриц одной размерности получается квадратная матрица той же размерности.

Приведём пример умножения матрицы размерности 4×3 на матрицу размерности 3×2, размерность произведения при этом будет 4×2.

В обратном порядке перемножить эти матрицы нельзя, так как умножение матрицы размерности 3×2 на матрицу размерности 4×3 не определено.

Покажем, что от перемены мест сомножителей, даже если умножение в обратном порядке возможно, результат может измениться.

Если , , то .

Но . Как видно, , то есть умножение матриц не обладает свойством коммутативности.

Транспонирование произведения двух матриц можно заменить умножением транспонированных сомножителей в обратном порядке, то есть имеет место равенство (AB)^Τ = B^ΤA^Τ. Это равенство пригодится нам при изучении квадратичных форм.

Его справедливость легко обосновать. Элемент матрицы B^ΤA^Τ, стоящий на пересечении i-й строки и j-го столбца, получается как сумма произведений элементов i-й строки матрицы B^Τ, то есть i-го столбца матрицы B, на соответствующие элементы j-го столбца матрицы A^Τ, то есть j-й строки матрицы A. Именно таким образом вычисляется элемент матрицы AB, стоящий на пересечении j-й строки и i-го столбца и совпадающий с элементом матрицы (AB)^Τ, стоящим на пересечении i-й строки и j-го столбца.

Квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы – нули, называется единичной и обозначается через E (или через E_n, если необходимо указать её порядок).

Единичные матрицы обладают замечательным свойством: умножение матрицы (слева или справа) на единичную матрицу подходящей размерности не изменяет исходную матрицу. Иными словами, если матрица А имеет размерность , то .

Например, , .

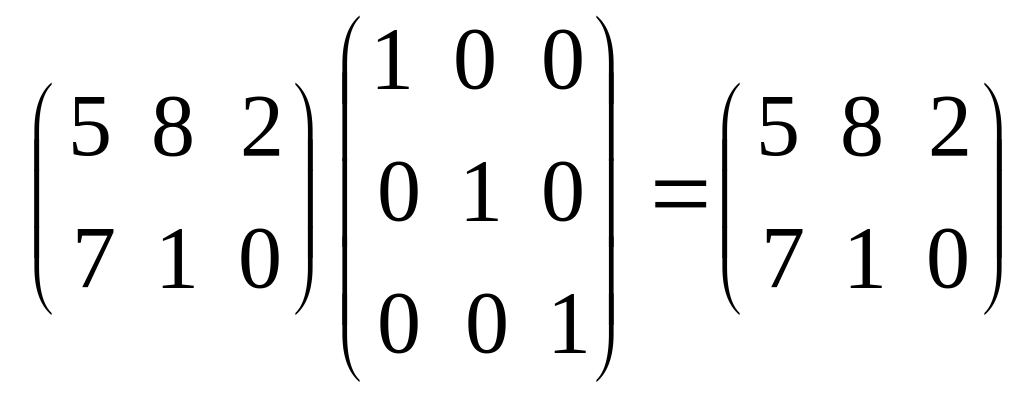Матрица, обозначаемая через A^–1, называется обратной по отношению к квадратной матрице A, если верны равенства: AA^–1= E и A^–1A = E.

Условие, при котором квадратная матрица имеет обратную, содержит понятие определителя квадратной матрицы.