
- •Министерство образования и науки рОссийской федерации
- •Кафедра высшей математики сПбГлту
- •Предисловие
- •Программа курса «Линейная алгебра»
- •Матрицы и определители Матрицы. Линейные операции над матрицами
- •Умножение матриц
- •Определители второго и третьего порядков
- •Свойства определителей
- •Формулы Крамера
- •Матричный метод решения систем линейных уравнений
- •Метод Гаусса
- •Приведение матрицы к каноническому виду
- •Решение систем линейных уравнений методом Гаусса
- •Пример. Пусть дана система
- •Ранг матрицы
- •Собственные числа и собственные векторы
- •Линейные пространства и линейные операторы Линейные пространства
- •Линейные операторы
- •Квадратичные формы Матричная запись квадратичной формы
- •Приведение квадратичной формы к каноническому виду
- •Знакоопределённые квадратичные формы
- •Элементы аналитической геометрии1
- •Векторы. Линейные операции над векторами
- •Координаты вектора
- •Скалярное произведение векторов
- •Прямая и плоскость в пространстве
- •Общее уравнение плоскости
- •Контрольные задания Контрольная работа № 1
- •Контрольная работа № 2
- •Комментарии к контрольным заданиям
- •Библиографический список
- •Оглавление
- •Алексеева Валентина Евгеньевна
- •194021, Санкт-Петербург, Институтский пер., 5
Контрольные задания Контрольная работа № 1
1 – 10. Решить систему уравнений тремя способами: по формулам Крамера, методом Гаусса-Жордана, средствами матричного исчисления. Сделать проверку правильности вычисления обратной матрицы.
1.
 2.
2.
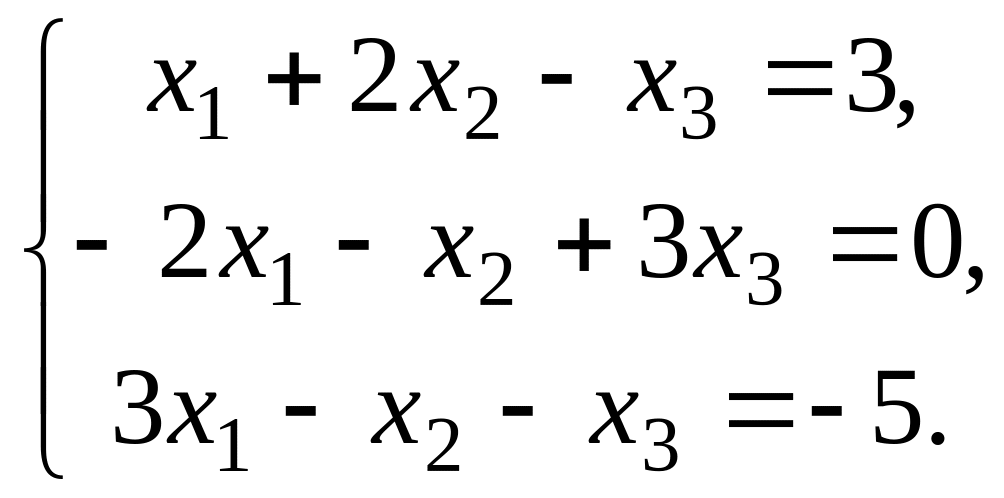
3.
 4.
4.

5.
 6.
6.

7.
 8.
8.

9.
 10.
10.
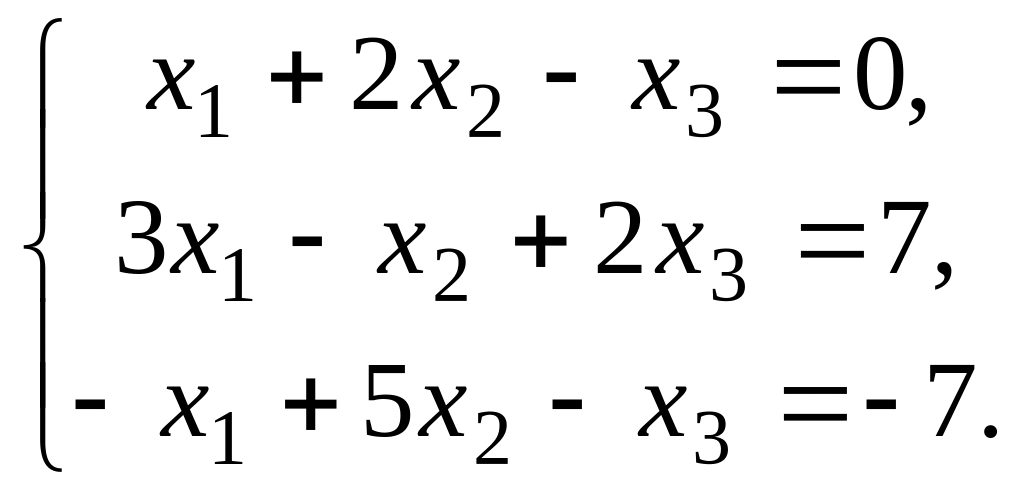
11 – 20. Даны векторы a, b, c и d. Показать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисе.
11. a (1, –1, 4 ), b (3, –2, –1 ), c (–2, 1, –1 ), d (5, –3, 6 ).
12. a (1, –2, 3 ), b (2, –1, –1 ), c (–1, 3, –1 ), d (3, 0, –5 ).
13. a (1, –5, 2 ), b (1, –4, –1 ), c (–2, 1, –3 ), d (4, –11, 7).
14. a (1, –2, 2 ), b (3, –5, –1 ), c (–1, 1, –2 ), d (5, –7, 3 ).
15. a (1, –3, 2 ), b (2, –5, –1 ), c (–3, 1, –2 ), d (7, –11, 0 ).
16. a (1, 2, –2 ), b (1, –1, 3 ), c (–2, 3, –1), d (–1, 4, –8 ).
17. a (1, 3, –1 ), b (2, –1, 4 ), c (–1, 2, –1 ), d (–3, –4, 1 ).
18. a (1, 4, –2 ), b (1, –1, –1 ), c (–4, 3, 1 ), d (–1, –9, 3).
19. a (1, 5, –1 ), b (1, 3, –2 ), c (–2, 1, 1), d (1, 1, –3 ).
20. a (1, 3, –1 ), b (2, –1, 5 ), c (–1, 2, –1 ), d (0, 7, –7).
21 – 30. Найти ранг матрицы.
21.
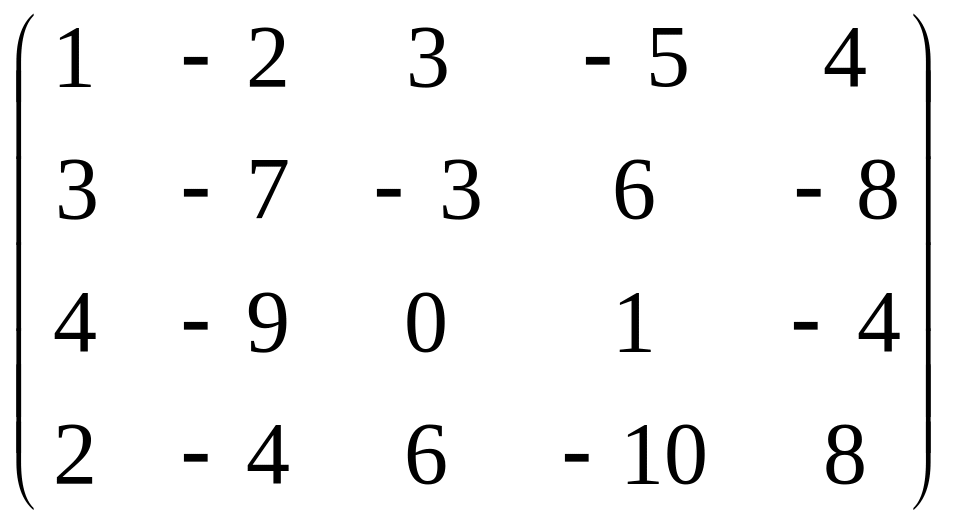 22.
22.
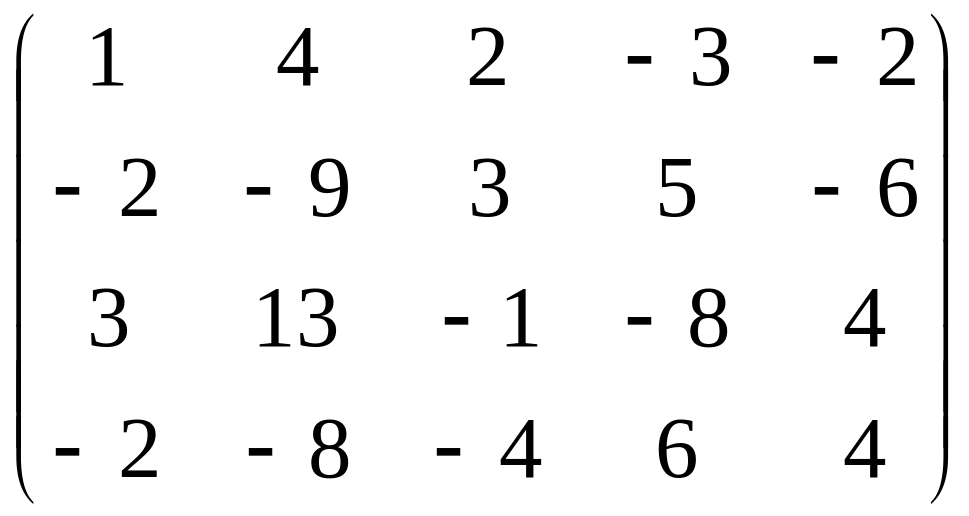
23.
 24.
24.
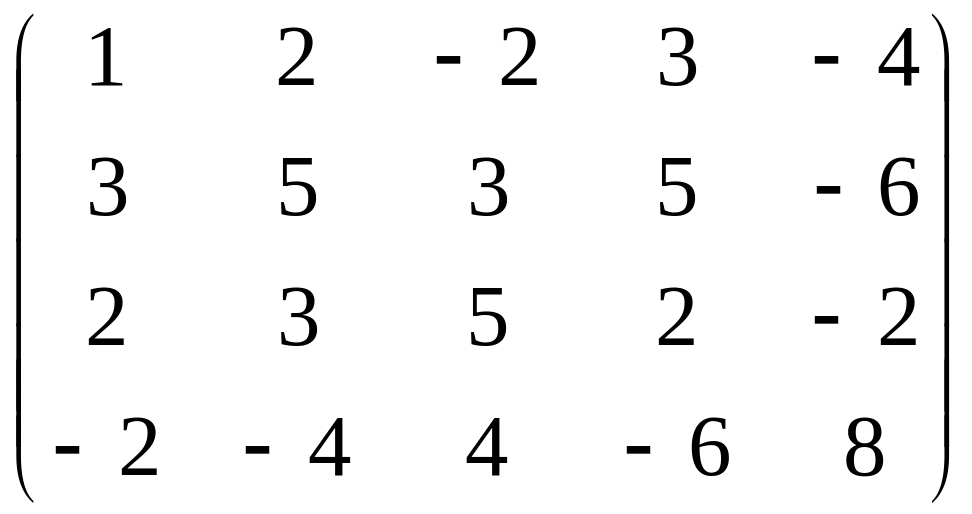
25.
 26.
26.

27.
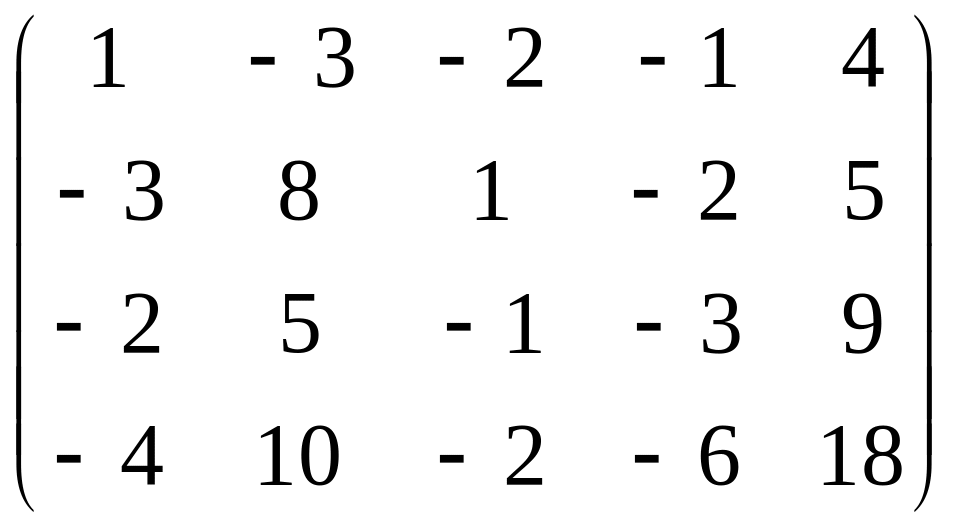 28.
28.
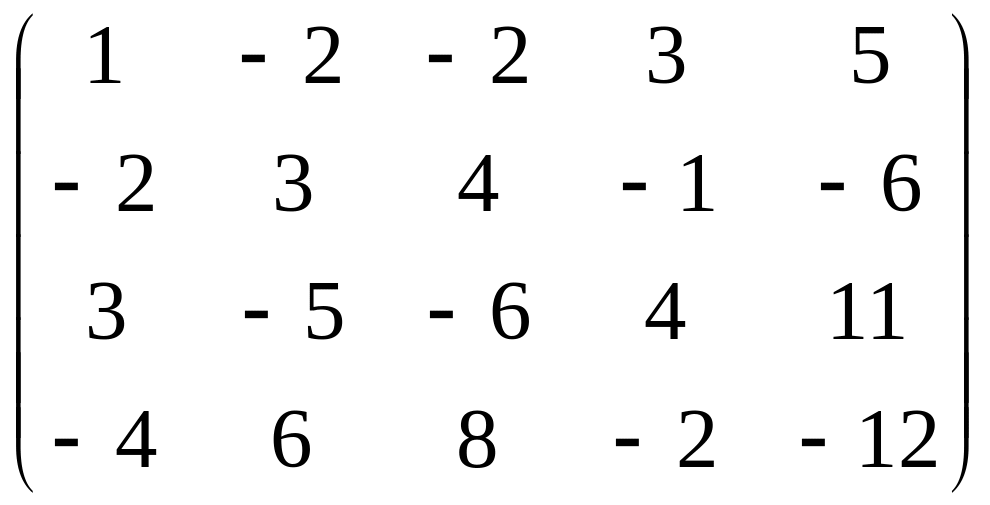
29.
 30.
30.

31 – 40. Являются ли данные векторы линейно независимыми? Если нет, укажите максимальное число линейно независимыми векторов из четырёх данных.
31.
![]() ,
32.
,
32.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
33.
![]() ,
34.
,
34.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
35.
![]() ,
36.
,
36.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
37.
![]() ,
38.
,
38.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
39.
![]() ,
40.
,
40.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
41 – 50. Выберите из данных двух систем совместную и найдите все её решения.
41.
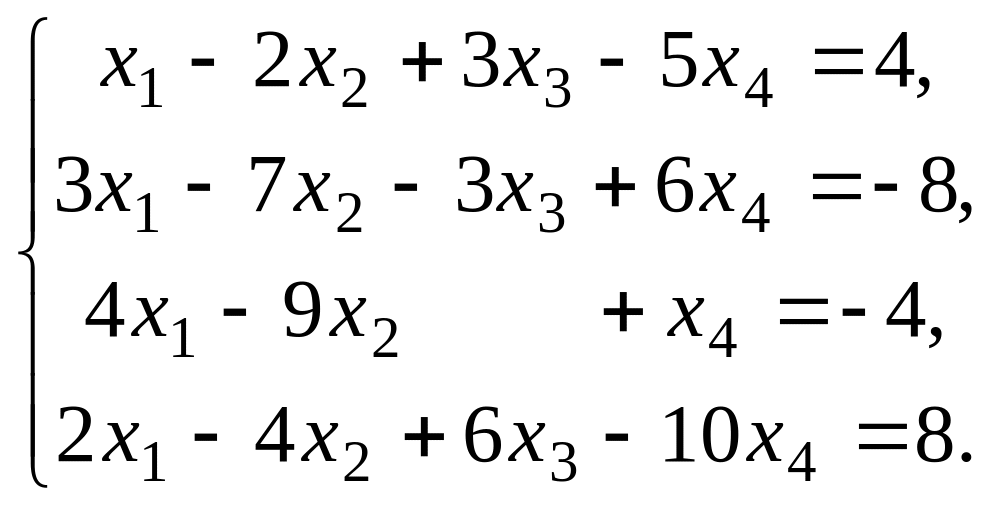

42.
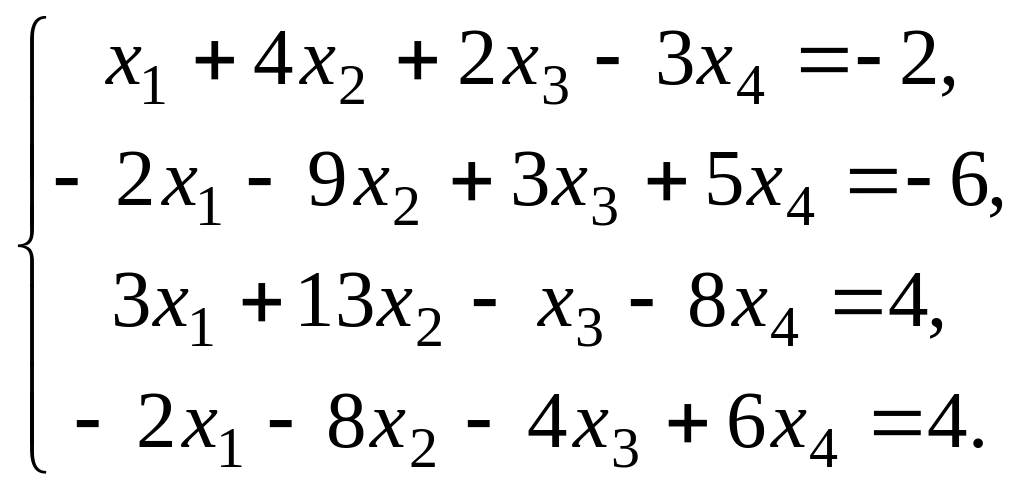

43.


44.


45.
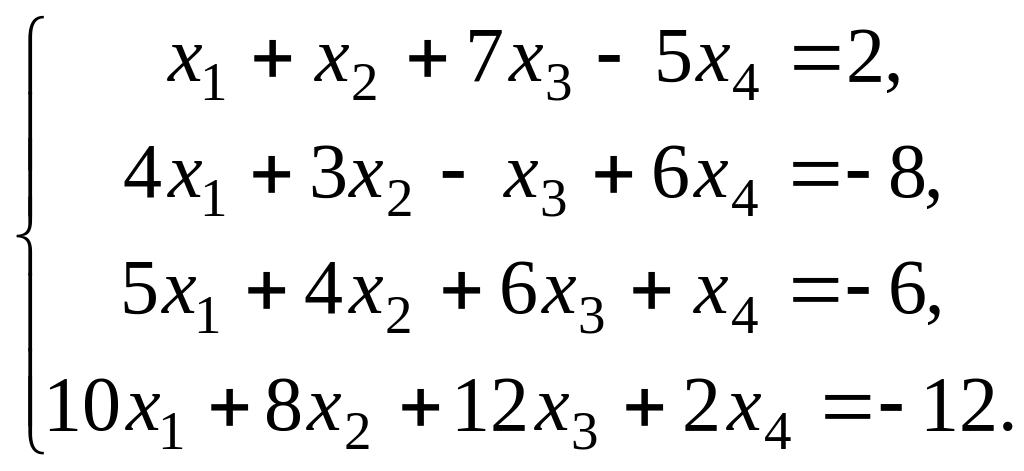

46.


47.
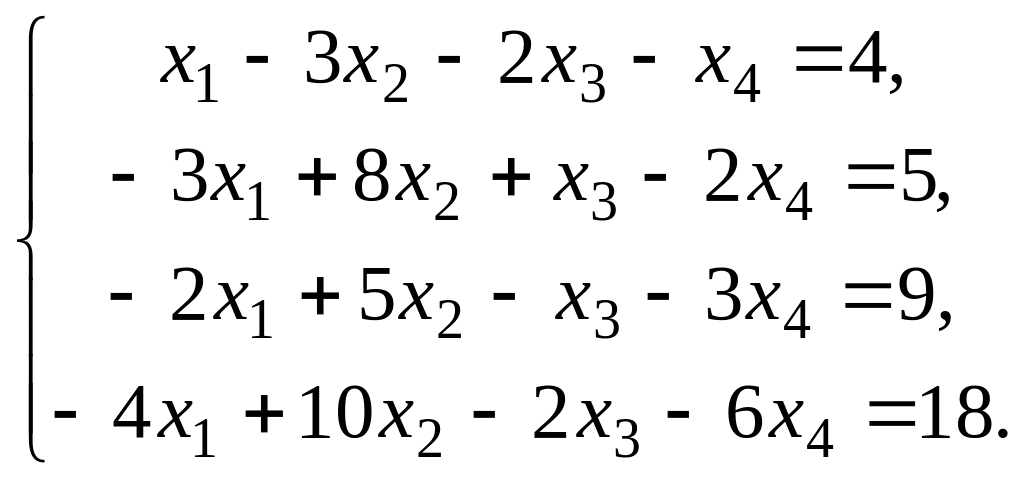

48.

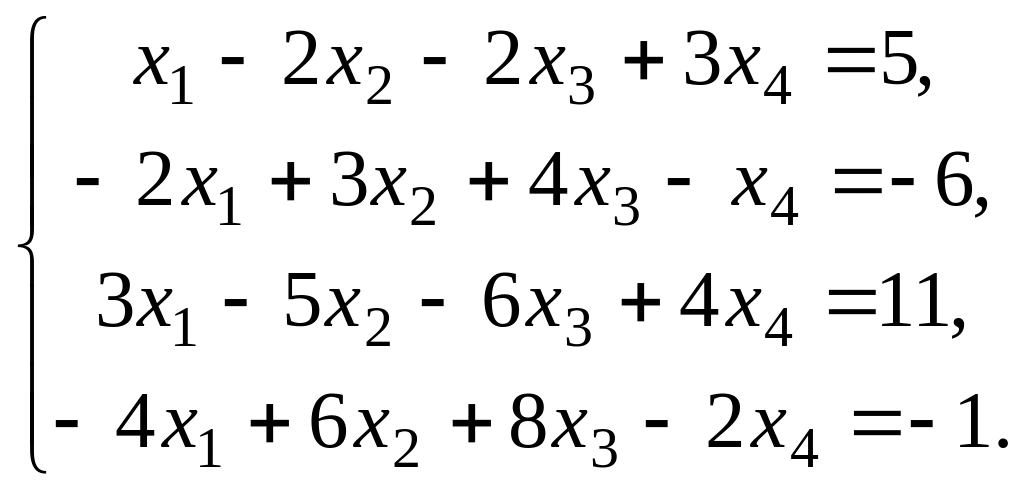
49.


50.


51 – 60. Имеет ли данная однородная система линейных уравнений ненулевые решения?
51.
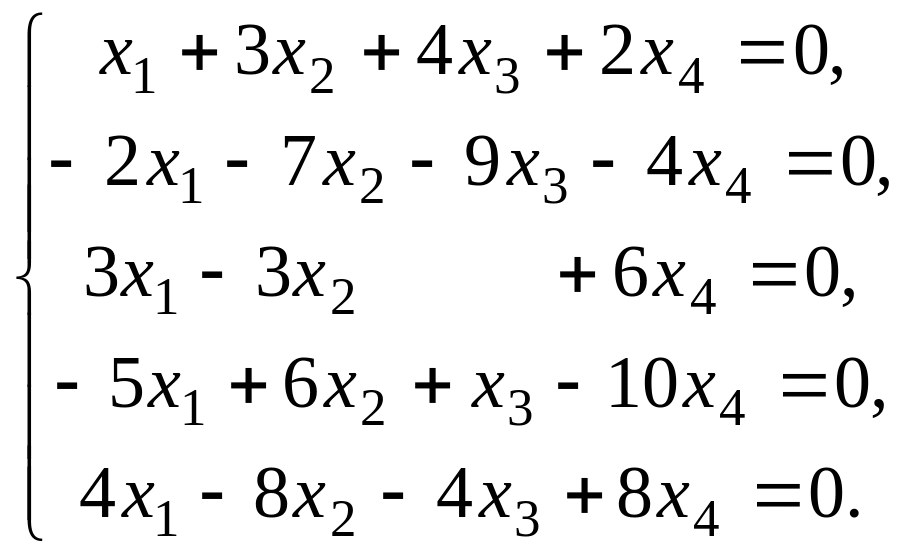 52.
52.

53.
 54.
54.

55.
 56.
56.

57.
 58.
58.
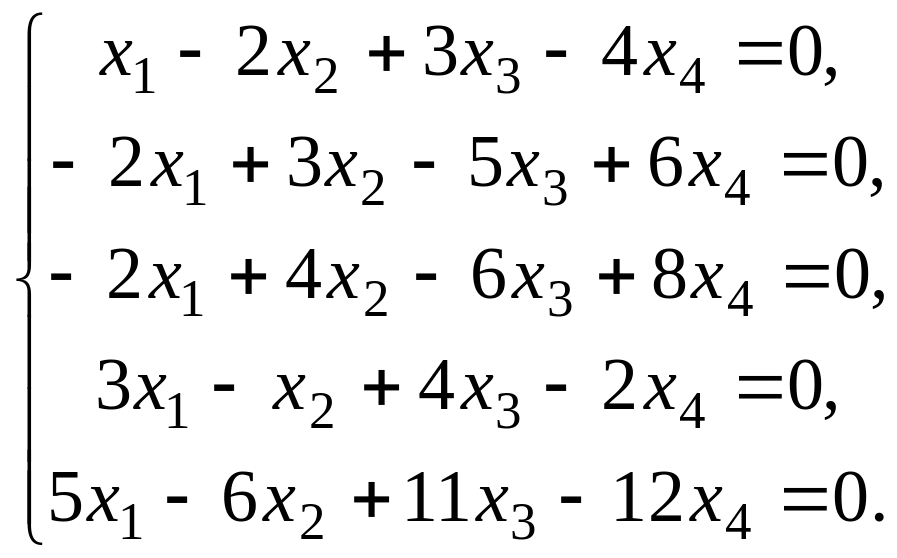
59.
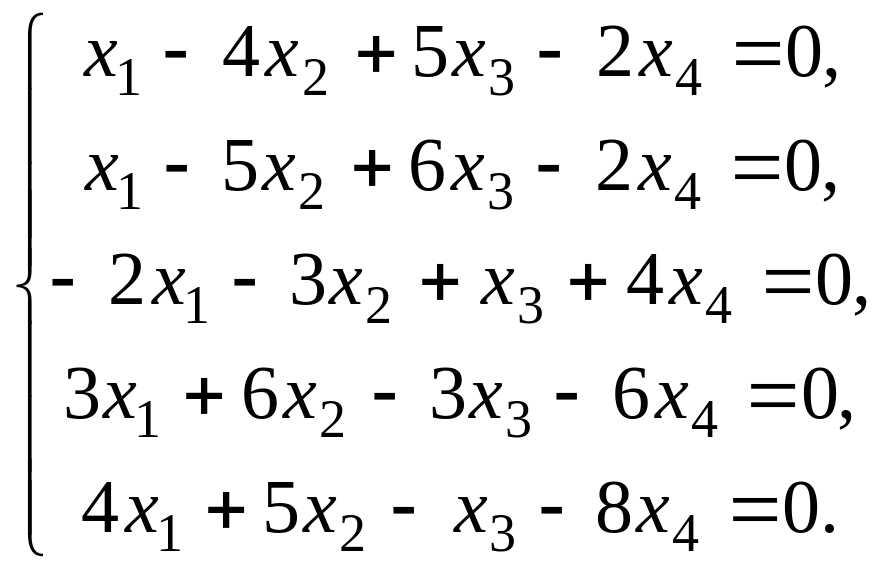 60.
60.

Контрольная работа № 2
61 – 70. Найти собственные числа и собственные векторы квадратной матрицы второго порядка.
61.
![]() 62.
62.
![]() 63.
63.
![]() 64.
64.
![]() 65.
65.
![]()
66.
![]() 67.
67.
![]() 68.
68.
![]() 69.
69.
![]() 70.
70.
![]()
71 – 80. Найти собственные числа и собственные векторы квадратной матрицы третьего порядка.
71.
 72.
72.
 73.
73.
 74.
74.
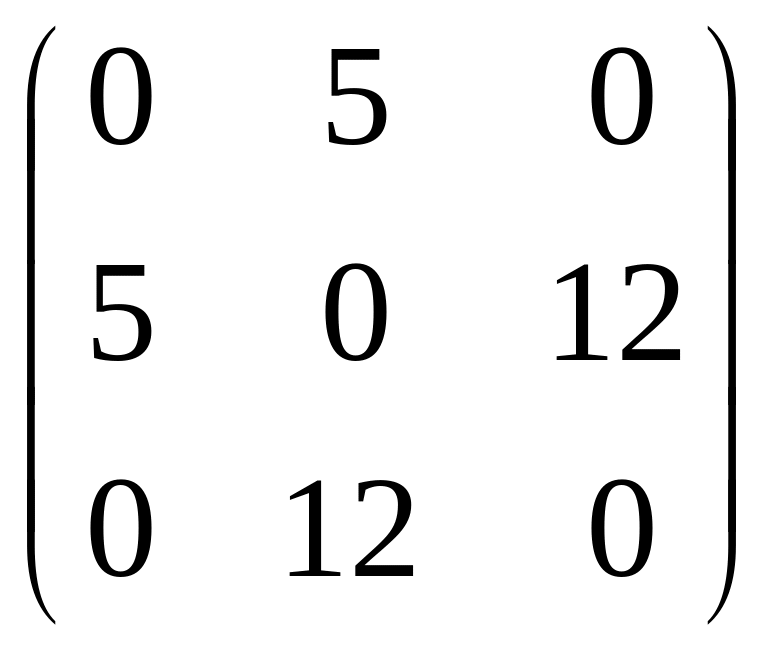
75.
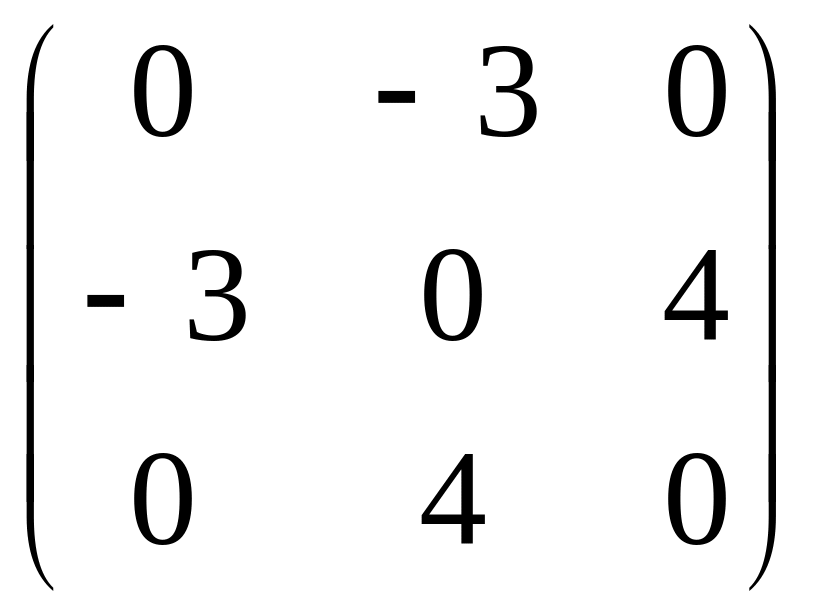 76.
76.
 77.
77.
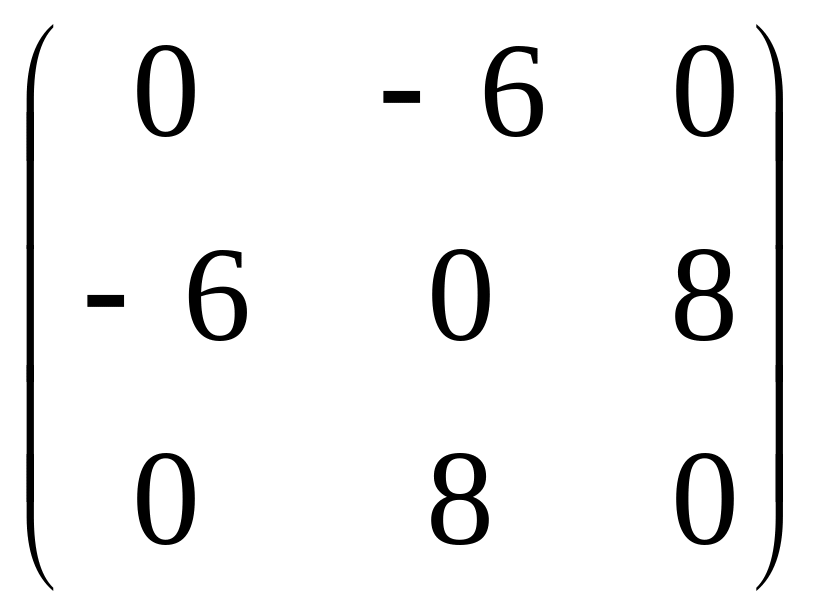
78.
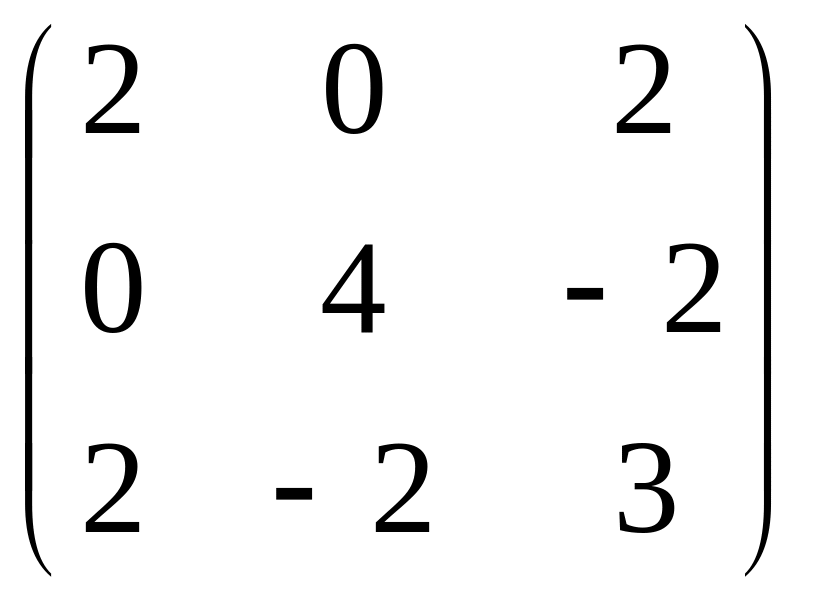 79.
79.
 80.
80.
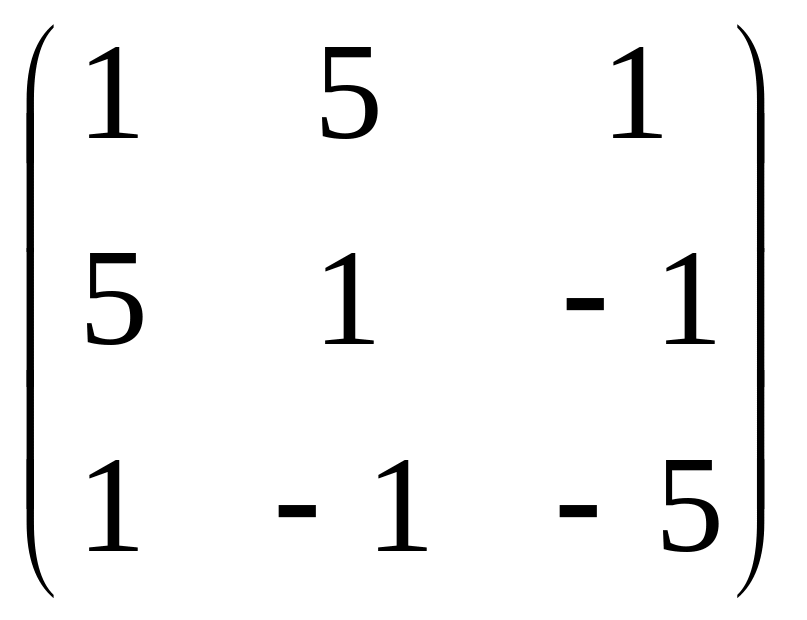
81 – 90. Привести квадратичную форму к стандартному виду двумя способами: методом Лагранжа и при помощи ортогонального преобразования. Выписать матрицы соответствующих преобразований. Определить, является ли данная квадратичная форма положительно или отрицательно определённой, полуопределённой, неопределённой.
81.
а)
![]() ;
82. а)
;
82. а)
![]() ;
83. а)
;
83. а)
![]() ;
;
б)
![]() .
б)
.
б)
![]() б)
б)
![]()
84.
а)
![]() ;
85. а)
;
85. а)
![]() 86.
а)
86.
а)
![]()
б)
![]() б)
б)
![]() б)
б)
![]()
87.
а)
![]() ;
88. а)
;
88. а)
![]() ;
;
б)
![]() .
б)
.
б)
![]() .
.
89.
а)
![]() ;
90. а)
;
90. а)
![]() ;
;
б)
![]() б)
б)
![]()
91
– 100. Даны
координаты точек A
и
B,
векторы
![]() и
и
![]() .
Являются ли векторы
и
перпендикулярными? Найти |
+
.
Являются ли векторы
и
перпендикулярными? Найти |
+![]() |.
Коллинеарны ли векторы
и
+
?
|.
Коллинеарны ли векторы
и
+
?
91.
A
(1,
0, –2);
B
(6, 1, –3);
(3, –2, 0);
= 2
![]() +3
+3![]() –
4
–
4![]() .
.
92. A (2, – 4, 3); B (– 8, –2, 5); (0, 1, –2); = 5 –2 + .
93. A (3, –3, 1); B (– 4, 2, 2); (1, 0, –3); = 6 – 5 +2 .
94.
A
(4,
–1, 2);
B
(0, 3, –1);
(–1, 2, 4);
![]() = 2
+3
–
.
= 2
+3
–
.
95. A (5, 0, –2); B (4, 2, 0); (–2, 3, 1); = + –2 .
96. A (–1, 2, 3); B (1, 1, 3); (4, 0, –1); = –2 + .
97. A (–2, 0, –14); B (4, 6, 1); (3, –1, 2); = – +3 +3 .
98. A (–3, 3, 1); B (4, 2, 3); (2, –3, 2); = 5 +2 –2 .
99. A (– 4, 2, 3); B (–1, 11, 3); (–3, 4, 1); = 5 +2 – .
100. A (–5, 1, 0); B (1, 0, –2); (0, 2, –1); = + – .
101
– 110. Даны
плоскость
![]() ,
вектор
,
вектор
![]() ,
точка M.
Найти: а) уравнение плоскости β, проходящей
через точку M
параллельно плоскости α; б) уравнение
плоскости γ, проходящей через начало
координат перпендикулярно вектору
;
в) канонические и параметрические
уравнения прямой, проходящей через M
перпендикулярно плоскости α. Принадлежит
ли точка M
открытому полупространству, определяемому
плоскостью γ и вектором
?
,
точка M.
Найти: а) уравнение плоскости β, проходящей
через точку M
параллельно плоскости α; б) уравнение
плоскости γ, проходящей через начало
координат перпендикулярно вектору
;
в) канонические и параметрические
уравнения прямой, проходящей через M
перпендикулярно плоскости α. Принадлежит
ли точка M
открытому полупространству, определяемому
плоскостью γ и вектором
?
101.
![]()
102.
![]()
103.
![]()
104.
![]()
105.
![]()
106.
![]()
107.
![]()
108.
![]()
109.
![]()
110.
![]()
