
- •«Теодолітна зйомка» Практична робота № 6
- •Порядок та послідовність виконання завдання:
- •Відомість обчислення координат
- •Література:
- •«Теодолітна зйомка» Практична робота № 6
- •Порядок та послідовність виконання завдання:
- •Відомість обчислення координат
- •«Теодолітна зйомка» Практична робота № 6
- •Порядок та послідовність виконання завдання:
- •Відомість обчислення координат
Відомість обчислення координат
 =
180˚(n-2)
=
180˚(n-2)
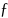 β
=
β
=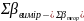
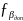 =
± 1,5·t’·
=
± 1,5·t’·

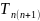 =
=
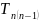 ±180˚-
±180˚-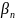
Δx=d·Cos(T)
ПнСх |
ПдСх |
ПдЗх |
ПнЗх |
+Δx |
-Δx |
-Δx |
+Δx |
+Δy |
+Δy |
-Δy |
-Δy |
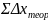 =0
=0
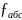 =
=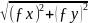 =
=
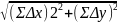
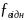 =
=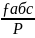 ≤
≤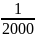
1) Якщо кути горизонтальні по ходу праві (внутрішні) то їх вписуємо у «Відомість замкнутого теодолітного ходу» в графу «2». У графі «1» назву точки. Наприклад, у нашому варіанті 6 точок (32, 22, 21, 11, 45, 46).Якщо кути ліві, як в нашому прикладі (див. рис. 70), то переводимо їх у праві за формулою:горизонтальний кут (лівий) = 360˚ - β , де β – це значення лівого кута за ходом теодолітної зйомки.
Підставимо у формулу:
360˚ - 302˚ 31,′2 = 57˚ 28,′8;
360˚ - 214˚ 17,′6 = 145˚ 42,′4;
360˚ - 202˚ 10,′0 = 157˚ 50,′0;
360˚ - 277˚ 0,′1 = 82˚ 59,′9;
360˚ - 240˚ 50,′9 = 119˚ 9,′1;
360˚ - 203˚ 13,′2 = 156˚ 46,′8.
Ми маємо випадок коли віднімаємо у 2-й дії кут 145˚ 42,′24″. Ці 24″ секунди треба перевести у мінути, тому 24 : 4 = 0,4′ (Рис. 71). Перевівши секунди у мінути, вписуємо отримані значення в колонку 2.

Рис. 71. Дії на мікрокалькуляторі, при перетворенні лівих кутів у праві
2) Знаходимо практичну суму горизонтальних кутів замкнутого теодолітного ходу.
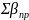 =
57˚
28,′8
+ 145˚
42,′4+
157˚
50,′0
+ 82˚
59,′9
+ 119˚
9,′1
+ 156˚
46,′8
= 719˚
57,′0
=
57˚
28,′8
+ 145˚
42,′4+
157˚
50,′0
+ 82˚
59,′9
+ 119˚
9,′1
+ 156˚
46,′8
= 719˚
57,′0
3) Проводимо ув’язку горизонтальних кутів полігону. Для цього знаходимо теоретичну суму кутів ( ) :
= 180˚(n - 2) ,
де, n – кількість виміряних кутів у полігоні.
У нашому прикладі 6 горизонтальних кутів:
= 180˚(6 - 2) = 720˚
4) Знаходимо кутову похибку, яка підтвердить достовірність польових досліджень, за формулою :
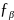 =
=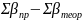 ,
,
де, – кутова похибка.
=719˚
57,′0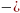 720˚
=
3′
720˚
=
3′
Внесення кутових поправок:
Вноситься в кожний кут порівно з протилежним знаком, тобто якщо похибка у зі знаком « », то додаємо її до виміряного горизонтального кута, якщо ж вона зі знаком «+», то навпаки її віднімаємо.
Поправки вносяться не в кожний виміряний кут, а лише в ті кути, до яких прилягають найкоротші відстані. Поправка вноситься у графу«3».
Спочатку вносять поправки на ті кути, які мають найбільше горизонтальне прокладання, або порівно розподіляють на всі кути, як в нашому прикладі:
3′ : 6 = + 0,5′
Вносимо в графу за знаком «+»
Наприклад:
57˚ 28,′8 + 0,5′ = 57˚ 29,′3 , або 57˚ 28,′8 + ( 0,5′) = 57˚ 28,′3 , якщо поправка за знаком « »
5) Вираховуємо за формулою допустиму поправку:
= ± 1,5·t′· ,
де, t′ - подвоєна точність теодоліта.
n – кількість виміряних кутів.
=
1,5·1′·
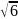 = 7′,2
= 7′,2
Якщо практична похибка допустима, то у виміряні кути вносять поправки, з таким розрахунком, щоб сума виправлених кутів була рівна теоретичній.
Для контролю із графи «4» додали всі кути. Їх сума дорівнювала .
6) Вираховуємо дирекцій ний кут, за формулою:
= ± 180˚ - де
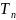 -
дирекційний кут;
-
дирекційний кут;
- горизонтальний кут;
n– кількість виміряних кутів.
Із
схеми перший дирекцій ний кут становить
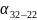 =
132˚22′,4. Вписуємо його у графу«5».
=
132˚22′,4. Вписуємо його у графу«5».
Далі вираховуємо дирекційний кут, за значенням врівноважених кутів (графа «4»):
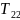 =
132˚24′,4
+ 180˚ ± 145˚
42,′9
= 166˚41,′5;
=
132˚24′,4
+ 180˚ ± 145˚
42,′9
= 166˚41,′5;= 166˚41,′5 + 180˚ ± 157˚ 50,′5 = 188˚51, ′0;
= 188˚51, ′0 + 180˚ ± 82˚ 60,′4 = 285˚50, ′6;
= 285˚50, ′6 + 180˚ ± 119˚ 9,′6 = 346˚41, ′0;
= 346˚41,′0 + 180˚ ± 156˚ 47,′3 = 9˚53,′7;
= 9˚53,′7 + 180˚ ± 57˚ 29,′3 = 132˚24,′4.
Якщо до дирекційного кута останньої лінії додати 180˚ і відняти кут у першій точці то повинні одержати початковий дирекцій ний кут першої лінії.
7) У «Відомість обчислення координат» записуємо горизонтальні проекції виміряних на місцевості ліній. У нашому прикладі їх 6 (203,15 м, 176,78м, 103,08 м, 174,10 м, 176,78 м, 194,18 м) ця сума P = 1028,07.
Для вирахування припростів координат дирекційні кути переводять у румби (рис. 72.).
1 – якщо дирекційний кут від 0˚ до 90˚ ,то r1 = α1, де r це румб
2 – якщо дирекційний кут від 90˚ до 180˚, то r2 =180˚ - α2
3 – якщо дирекційний кут від 180˚ до 270˚, то r3 = α3 - 180˚
4 – якщо дирекційний кут від270˚ до 360˚, то r4 =360˚ - α4
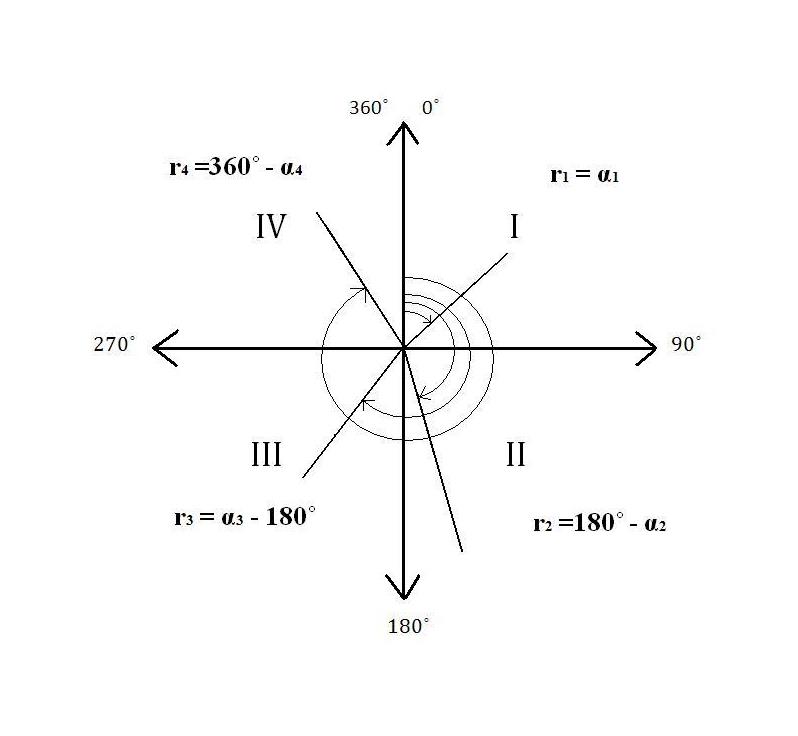
Рис. 72. Чверті румбів
Орієнтуючись на рис. 72 беремо із графи «5» значенняT кутів.
Наприклад кут 132˚24′,4 – він знаходиться у другій чверті тому, якщо підставити його у формулу, набуде вигляду:
180˚ - 132˚24′,4 = Пд Сх 47˚ 35′,6 (відповідно і для решти кутів);
180˚ - 166˚41,′5 = ПдСх 13˚ 18, ′5;
188˚51, ′0 - 180˚ = ПдЗх 8˚ 51, ′0;
360˚ - 285˚50, ′6 = ПнЗх 105˚ 50, ′6;
360˚ - 346˚41,′0 = ПнЗх 13˚ 19, ′0;
9˚53,′7 = ПнСх 9˚ 53, ′7.
9) Вираховуємо прирости координат Δx та Δy за формулами:
Δx=d·Cos(r)
Δx=d·Sin (r) , де
d – горизонтальне прокладення.
Cos(r), Sin (r) = косинус або синус румба.
Тоді на калькуляторі виконуємо такі дії :
Δx = 203,15 * (cos47˚ 35′,6) = 203,15 * 0,73 = -137,00
Беремо cos на калькуляторі і набираємо значення румба з графи «6» або значення дирекційного кута з графи «5» ( Рис. 74, 75). Значення будуть ідентичні.
На калькуляторі обов’язково повинен стояти значок D – degrees (англ. –«градуси»), (рис. 73).
Якщо ж замість значка D обрані R (radian) або G (gradient) то за допомогою кнопки Mode обираємо D(degrees).

Рис. 73. Налаштування калькулятора
У нашому прикладі ми обираємо косинус дирекційного кута (рис. 74):
1)203,15 * (cos132˚24′,4 ) = 203,15 * 0,73 = -137,00
2) 176,78 * (cos166˚41,′5 ) = -172,03
3) 103,08 * (cos188˚51, ′0 ) = -101,85
4) 174,10 * (cos285˚50, ′6 ) = 47,53
5) 176,78 * (cos346˚41,′0) = 172,02
6) 194,18 * (cos9˚53,′7 ) = 191,29

Рис. 74. Дії на калькуляторі при взятті косинуса дирекційного кута

Рис. 75. Дії на калькуляторі при взятті косинуса румба
Чинимо відповідні дії з синусами та заносимо отримані результати у графи«8» та «10».

Рис. 4 Дії на калькуляторі при взятті синуса румба
Якщо значення румба наприклад ПдСх 47˚ 35′,6 то його значення по таблиці 3 буде зі знаком « » ( табл. 3).
Таблиця 3
ПнСх |
ПдСх |
ПдЗх |
ПнЗх |
+Δx |
-Δx |
-Δx |
+Δx |
+Δy |
+Δy |
-Δy |
-Δy |
10) Розкидаємо поправку.
Всі значення з графи «8» зі знаком « » та «+» додаємо окремо одне від одного, одержані результати порівнюємо та отримуємо похибку:
+410,88 = 410,84
Аналогічні дії проводимо у графі «10».
Поправка знаходиться шляхом віднімання від суми додатних значень суму від’ємних:
410,84 – 410,88 = -0,04.
Поправку розкидаємо на найменші значення d з протилежним знаком. Тіж дії виконуємо у графі «11».
Врівноважені прирости записуємо відповідно у графи «12» і «13».
11) Потрібно також здійснити контроль:
= 0
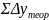 =
0
=
0
Δx: 410,86 - 410,86 = 0,00
Δy: 224,04 - 224,04 = 0,00
Для
контролю в замкнутому полігоні знаходять
алгебраїчну суму за Δx
і Δy,
яка буде виражати практичну похибку в
приростах координат (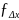 і
і
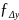 ). Щоб переконатись у достовірності
виконання вимірювань знаходять абсолютну
похибку (
)
за формулою:
). Щоб переконатись у достовірності
виконання вимірювань знаходять абсолютну
похибку (
)
за формулою:
= = , а відносну = ≤ , де,P – периметр полігону (сума всіх сторін в багатокутнику)
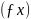 -
обчислені прирости по Δx
-
обчислені прирости по Δx
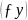 -
обчислені прирости по Δy
-
обчислені прирости по Δy
Наші поправки Δx = - 0,04 , Δy = +0,01. Підставляємо у формулу:
=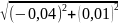 =
=
 = 0,04
= 0,04
=
=
 ~
~

= ≤
Тобто допустима у тому випадку коли відношення буде не більшим за
12)Координати точок вираховують за формулами:
Xк = Xк-1± Δx
Yк = Yк-1 ± Δy
Записуємо зі схеми полігону координати X таY і вписуємо у графи «14» і «15».
Наприклад:
X = 10187,0 Y = 10200,0
X = 10050,0 Y = 10350,0
Обрахунок проводимо таким чином:
1) 10187,00 + (-137,00) = 10050,0
2) 10050,0 + (-172,03) = 9877,98
3) 9877,98 + (-101,85) = 9776,14
4) 9776,14 + 47,53 = 9823,68
5) 9823,68 + 10187,00 = 9995,71
6) 9995,71 + 191,29 = 10187,00
Якщо до координати останньої точки в полігоні додати чи відняти приростки на останню лінію, то одержимо координати першої точки. Це і буде контролем вирахування координат.
Ті самі дії з відповідними числами проводимо з координатамиY.
