1.3.4 Карта долей несоответствующих единиц продукции (p-карта)

В таблице 3 приведены формулы для построения p-карт.

Таблица 3 - Формулы контрольных границ p-карт

Статистика	Центральная линия (CL)	3σ-е контрольные границы (UCL, LCL)
p

Если LCL<0, то граница на карту не наносится и в анализе не участвует.

Как видно из таблицы 3, положение контрольных границ зависит от объема выборок (подгрупп). Если число контролируемых единиц в каждой подгруппе различно, должны быть рассчитаны контрольные границы отдельно для каждого объема выборки. Однако, если объем выборок меняется несущественно, можно ограничиться одним набором контрольных границ, основанным на среднем объеме подгруппы. Для практических целей достаточно, если объемы выборок находятся в пределах ±25% целевого объема выборок. В этом случае в качестве n принимается средний объем выборок.

Используют контрольную p-карту аналогично -карте. Считается, что процесс находится в состоянии статистической управляемости, если все точки p-карты расположены внутри контрольных границ без выбросов, указывающих на наличие особых причин. Точки, выходящие за контрольные границы исключают, определяют новые контрольные границы, повторно строят карту. Процесс повторяется до тех пор, пока последняя из построенных p-карт не укажет на статистическую управляемость.

1.3.5 Пример построения и анализа -карты

В таблице 4 приведены результаты измерений сопротивлений 25 выборок резисторов (k=25), объемом 5 штук каждая (n=5). Требуется привести технологический процесс производства резисторов номинальным сопротивлением 1кОм и максимально допустимой погрешностью ±5% в статистически управляемое состояние, после чего оценить его возможность производить резисторы с указанными параметрами, сделать выводы о необходимости настройки либо модернизации оборудования. Вероятная доля дефектных резисторов не должна превышать 1%.

Найденные средние значения и размахи выборок также занесены в таблицу 4.

Определим среднее значение размахов выборок.

.

Таблица 4 – Данные технологического процесса

Номер выборки	Сопротивление					Среднее ( )	Размах (R)
	x1	x2	x3	x4	x5
1	0.995	0.999	1.013	1.005	1.001	1.003	0.018
2	1.011	0.991	0.983	0.982	1.016	0.996	0.034
3	0.990	1.010	1.058	0.985	0.989	1.006	0.073
4	1.011	1.013	1.007	1.020	0.983	1.007	0.037
5	1.015	0.998	1.017	1.008	1.006	1.009	0.019
6	1.007	1.001	0.982	0.987	1.017	0.999	0.035
7	1.003	0.988	1.001	1.016	1.005	1.003	0.028
8	0.988	1.005	0.986	0.988	0.984	0.990	0.021
9	0.982	0.981	1.016	1.017	1.001	1.000	0.036
10	0.988	1.017	1.016	0.988	1.009	1.003	0.029
11	1.000	1.011	1.004	1.006	0.982	1.001	0.028
12	1.004	1.002	1.011	0.980	1.011	1.002	0.031
13	1.019	1.004	0.984	1.013	1.015	1.007	0.034
14	1.005	1.009	0.990	0.993	1.003	1.000	0.019
15	1.018	0.981	0.997	1.017	1.012	1.005	0.036
16	1.004	0.996	1.011	1.003	1.010	1.005	0.014
17	0.999	0.997	0.982	1.007	1.009	0.999	0.027
18	0.990	0.980	1.012	0.987	0.986	0.991	0.031
19	0.991	0.983	1.012	1.008	1.005	1.000	0.030
20	0.990	0.991	1.008	1.002	0.994	0.997	0.018
21	1.009	0.984	0.988	0.999	0.987	0.993	0.024
22	0.992	0.993	1.019	1.003	0.983	0.998	0.036
23	0.997	0.984	1.016	1.018	1.010	1.005	0.034
24	1.001	0.994	1.017	1.003	1.010	1.005	0.022
25	0.998	0.984	1.010	1.005	1.012	1.002	0.028

Находим координаты центральной линии (CL), верхней (UCL) и нижней (LCL) контрольных границ по формулам, приведенным в таблице 1. Коэффициенты формул приведены в таблице 2.

.

.

(LCL отсутствует).

Строим R-карту (рисунок 3).

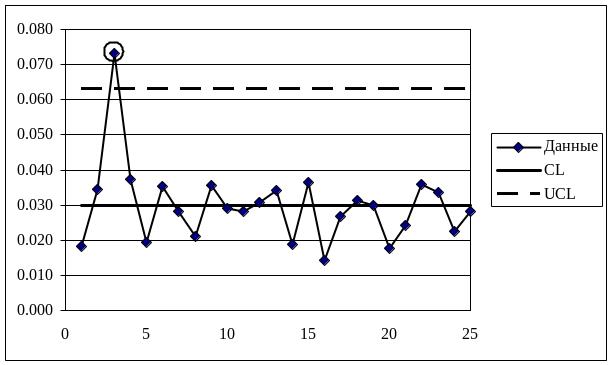
Рисунок 3 – R-карта (оригинальные данные)

Точка, соответствующая выборке номер 3, выходит за UCL, что говорит о том, что процесс находится в статистически неуправляемом состоянии. В момент изготовления резисторов из партии номер 3 на технологический процесс действовали особые (неслучайные) факторы, которые следует найти и устранить. Необычных структур расположения точек, могущих указывать на наличие других особых факторов, на R-карте не наблюдается. Исключаем выборку номер 3 из дальнейшего рассмотрения. Рассчитываем новые значения CL, UCL, LCL.

;

;

;

(LCL отсутствует).

Вновь полученная R-карта указывает на статистическую управляемость процесса (рисунок 4).

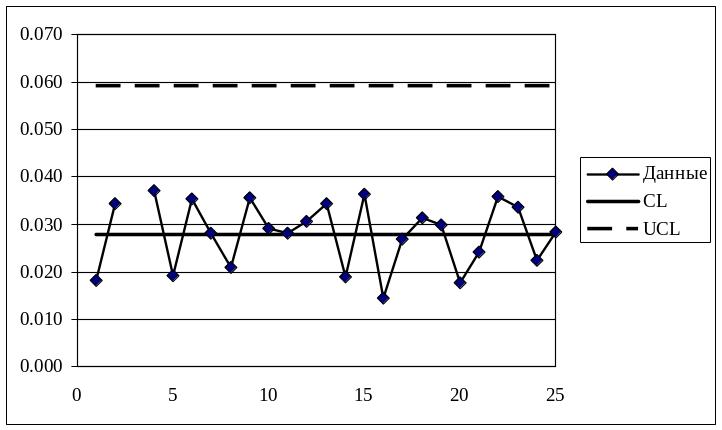
Рисунок 4 – R-карта (исключена выборка номер 3)

Вычисляем CL, UCL, LCL для -карты и строим -карту (рисунок 5). При вычислениях и построении точку 3 из первоначальной выборки исключаем.

;

;

.

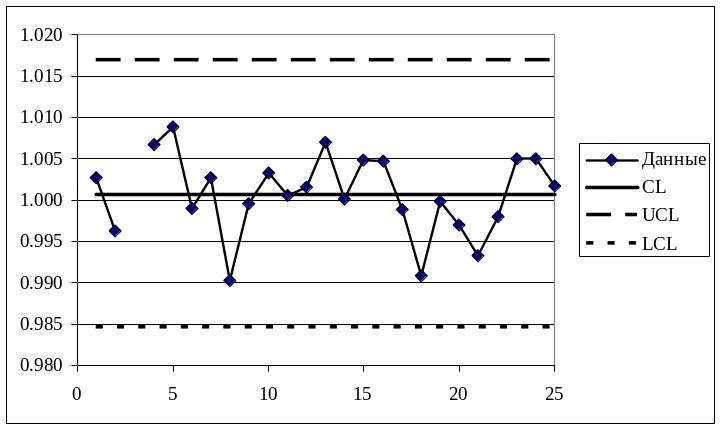
Рисунок 5 – -карта (исключена выборка номер 3)

На вновь полученной R-карте и на -карте все точки лежат внутри контрольных границ. Необычных структур расположения точек не наблюдается. Таким образом, карты, приведенные на рисунках 4 и 5, демонстрируют статистическую управляемость технологического процесса.

Оценим возможность данного процесса производить резисторы с заданными параметрами. Для этого вычислим индекс возможностей технологического процесса PCI.

Определим верхнее UTL и нижнее LTL допустимое значение контролируемого параметра:

UTL=1.05;

LTL=0.95.

Оценку среднеквадратического отклонения определим с помощью коэффициента 1/d₂, взятого из таблицы 2 для n=5:

.

.

Поскольку PCI больше 1.33, считаем, что процесс способен выпускать резисторы требуемого номинала с требуемой точностью. В тоже время, так как процесс находится в статистически управляемом состоянии и PCL лишь незначительно превышает величину 1.33, существенно улучшить процесс, и, например, перейти к выпуску резисторов с погрешностью 2.5% вероятно не удастся без модернизации технологического оборудования.

Определим величины коэффициентов точности и настроенности:

;

.

Ввиду того, что коэффициенты слишком малы, установить по номограмме (рисунок 2) значение вероятной доли дефектных резисторов не представляется возможным. Однако, можно уверенно утверждать, что она меньше установленной в задании величины 1%. Кроме того, смещение центра настройки от номинального значения контролируемого параметра составляет 0.1%. Дополнительная настройка процесса не требуется.