28) Точечные оценки параметров генеральной совокупности по выборке, их свойства.

Пусть  — случайная выборка из распределения, зависящего от

параметра . Тогда статистику , принимающую значения в , называют точечной оценкой параметра

Оценка называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности:

,

где обозначает математическое ожидание в предположении, что  — истинное значение параметра (распределения выборки ).

Оценка называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок.

Оценка называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности: ,

по вероятности при .

Оценка называется сильно состоятельной, если ,

почти наверное при

29) Точечные оценки для математического ожидания генеральной совокупности.

Точечная оценка математического ожидания определяется по формуле                                                            

30) Точечные оценки для дисперсии генеральной совокупности.

Точечная оценка дисперсии определяется по формуле

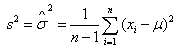
31) Интервальные оценки. Доверительный интервал. Нахождение доверительного интервала для математического ожидания генеральной совокупности с нормальным законом распределения.

Пусть - неизвестный параметр генеральной совокупности. По сделанной выборке по определенным правилам находятся числа и такие чтобы выполнялось неравенство:

Интервал является доверительным интервалом для параметра , а число - доверительной вероятностью или надежностью сделанной оценки. Обычно надежность задается заранее, причем выбираются числа близкие к 1 (0.95, 0.99 или 0.999).

Пусть генеральная совокупность описывается случайной величиной x, распределение которой зависит от скалярного параметра q. Пусть, далее, и две функции выборки такие, что всегда и .

( ) со случайными границами называют доверительным интервалом для неизвестного параметра q с доверительной вероятностью b.

32) Метод статистической проверки гипотез.

Пусть задана случайная выборка — последовательность объектов из множества . Предполагается, что на множестве существует некоторая неизвестная вероятностная мера  .

Методика состоит в следующем.

1. Формулируется нулевая гипотеза  о распределении вероятностей на множестве  . Гипотеза формулируется исходя из требований прикладной задачи. Чаще всего рассматриваются две гипотезы — основная или нулевая и альтернативная 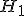 . Иногда альтернатива не формулируется в явном виде; тогда предполагается, что  означает «не  ». Иногда рассматривается сразу несколько альтернатив. В математической статистике хорошо изучено несколько десятков «наиболее часто встречающихся» типов гипотез, и известны ещё сотни специальных вариантов и разновидностей. Примеры приводятся ниже.

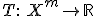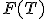2. Задаётся некоторая статистика (функция выборки) , для которой в условиях справедливости гипотезы выводится функция распределения и/или плотность распределения  . Вопрос о том, какую статистику надо взять для проверки той или иной гипотезы, часто не имеет однозначного ответа. Есть целый ряд требований, которым должна удовлетворять «хорошая» статистика  . Вывод функции распределения при заданных  и  является строгой математической задачей, которая решается методами теории вероятностей; в справочниках приводятся готовые формулы для  ; в статистических пакетах имеются готовые вычислительные процедуры.

3. Фиксируется уровень значимости — допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки. Это должно быть достаточно малое число . На практике часто полагают .

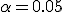4. На множестве допустимых значений статистики  выделяется критическое множество  наименее вероятных значений статистики  , такое, что 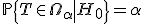. Вычисление границ критического множества как функции от уровня значимости является строгой математической задачей, которая в большинстве практических случаев имеет готовое простое решение.

5. Собственно статистический тест (статистический критерий) заключается в проверке условия:

   • если , то делается вывод «данные противоречат нулевой гипотезе при уровне значимости  ». Гипотеза отвергается.

   • если , то делается вывод «данные не противоречат нулевой гипотезе при уровне значимости  ». Гипотеза принимается.

Итак, статистический критерий определяется статистикой  и критическим множеством  , которое зависит от уровня значимости .