Система двух случайных величин.Функция распределения системы двух случайных величин, ее свойства.
Упорядоченную пару (X, Y) с. в. X и Y , заданных на одном и том же пространстве элементарных событий, называют двумерной случайной величиной или системой двух слу-
чайных величин.
Функцией распределения системы двух случайных величин называется функция двух аргументов F(x, y), равная вероятности совместного выполнения двух неравенств X<x, Y<y.
свойства функции распределения системы двух случайных величин:
1) Если один из аргументов стремится к плюс бесконечности, то функция распределения системы стремится к функции распределения одной случайной величины, соответствующей другому аргументу.
2) Если оба аргумента стремятся к бесконечности, то функция распределения системы стремится к единице.
3) При стремлении одного или обоих аргументов к минус бесконечности функция распределения стремится к нулю.
4) Функция распределения является неубывающей функцией по каждому аргументу.
Система двух случайных величин непрерывного типа.Плотность вероятности, ее свойства.
Непрерывные
случайные величины
называются независимыми, если
- соответственно плотности распределения
вероятностей случайных величин
.
В
этом случае
где F1(x) и F2(y) — соответственно функции распределения величин и . Зная функцию распределения F(х,у) двумерной случайной величины , легко найти как функцию распределения, так и плотность распределения каждой из случайных величин , в отдельности.
Действительно,
пусть F1(x)
- функция распределения случайной
величины
.
Тогда
. Так как в этом случае может принимать
любое значение, то ясно, что
Следовательно,
по формуле имеем
Дифференцируя
последнее равенство по x,
согласно правилу дифференцирования
интеграла по переменной верхней границе
получим
Аналогичным
образом получаем
и,
следовательно,
.
Таким образом, чтобы получить плотность
распределения одной из составляющих
двумерной случайной величины, надо
проинтегрировать в границах от -∞ до
+∞ плотность распределения системы
по переменной, соответствующей другой
случайной величине.
Условные законы распределения случайных величин.
Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение, называется условным законом распределения.
Условный закон распределения можно задавать как функцией распределения так и плотностью распределения. Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины.
Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корелляции.
Числа, назначение которых в сжатом виде характеризовать основные особенности распределений случайных величин, называются числовыми характеристиками. Характеристикой зависимости между случайными величинами служит математическое ожидание произведения отклонений и от их центров распределений (так иногда называют математическое ожидание случайной величины), которое называется корреляционным моментом или ковариацией:
Для вычисления корреляционного момента дискретных величин используют формулу:
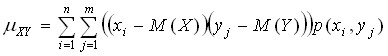
а для непрерывных величин – формулу:
