16. Критерий независимости случайных величин. Математическое ожидание произведения независимых случайных величин.

Случайная величина называется независимой от случайной величины , если закон распределения величины не зависит от того, какое значение приняла величина .

Для непрерывных случайных величин условие независимости от может быть записано в виде:

при любом . Напротив, в случае, если зависит от , то

Докажем, что зависимость или независимость случайных величин всегда взаимны: если величина не зависит от Y . Действительно, пусть не зависит от X:

Имеем:

,откуда, принимая во внимание (8.5.1), получим:

что и требовалось доказать.

Так как зависимость и независимость случайных величин всегда взаимны, можно дать новое определение независимых случайных величин.

Случайные величины и называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины и называются зависимыми.

Для независимых непрерывных случайных величин теорема умножения законов распределения принимает вид: т. е. плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему.

Мат ожидание. Произведением kX случайной величины Х на постоянную величину k называется новая случайная величина Z=kX, которая с теми же вероятностями, что и Х, принимает значения, равные произведениям значений случайной величины Х на k, т.е. =xi2.

17. Начальные моменты случайной величины. Математическое ожидание и его свойства.

Начальным моментом порядка s называется математическое ожидание степени s С.В. X:

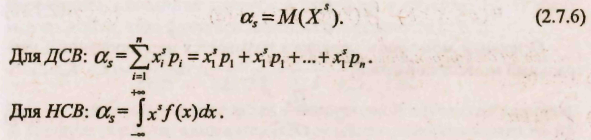
При s=l: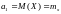 , то есть, первый начальный момент - это ма­тематическое ожидание СВ.

Математическим ожиданием (или средним значением) (или ) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений. Математическое ожидание непрерывной случайной величины X с плотностью вероятности 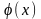, находится по формуле ,

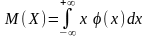1. Математическое ожидание постоянной величины равно самой постоянной: M(C) = C.

2. Постоянный множитель можно выносить за знак математического ожидания: M(CX) = CM(X).

3. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых: M(X+Y+Z) = M(X)+M(Y)+M(Z).

4. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий: M(XЧYЧZ) = M(X)ЧM(Y)ЧM(Z).

18. Центральные моменты случайной величины.Дисперсия и ее свойства.

Центральным моментом порядка s СВ X называется математиче­ское ожидание степени s, соответствующей центрированной СВ:

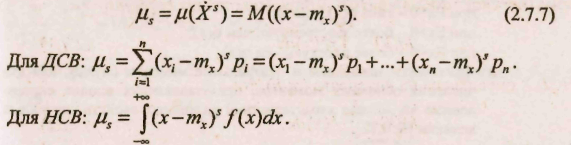
При вычислении центральных моментов пользуются формулами связи между центральными и начальными моментами:

Дисперсией (рассеянием) 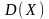(или ) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: .

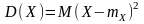1) Дисперсия постоянной величины равна нулю.

2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.

4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.