
- •Пространство элементарных событй. Случайные события. Алгебра событий.
- •Статистический подход к введению понятия вероятности.Классическое определение вероятности.
- •Теоремы сложения и умножения вероятностей.
- •Интегральная теорема Мавра-Лапласа и ее приложения.
- •Распределения Пуассона как предельный случай биномиального распределения.
- •Случайные величины дискретного типа. Ряд распределения. Наиважнейшие примеры.
- •Функция распределения случайной величины, ее свойства.
- •Случайные величины непрерывного типа. Наиважнейшие примеры.
- •Плотность вероятности случайной величины, ее свойства.
- •Критерий независимости случайных величин. Математическое ожидание произведения независимых случайных величин.
- •Начальные моменты случайной величины. Математическое ожидание и его свойства.
- •Центральные моменты случайной величины.Дисперсия и ее свойства.
- •Система двух случайных величин.Функция распределения системы двух случайных величин, ее свойства.
- •Система двух случайных величин непрерывного типа.Плотность вероятности, ее свойства.
- •Условные законы распределения случайных величин.
- •Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корелляции.
- •22) Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции.
- •23) Распределение основных дискретных случайных величин.
- •24) Неравенство Чебышева.
- •25)Теорема Чебышева.
- •26) Центральная предельная теорема.
- •27) Генеральная совокупность. Выборка. Статистический ряд. Гистограмма. Статистическая функция распределения.
- •28) Точечные оценки параметров генеральной совокупности по выборке, их свойства.
- •29) Точечные оценки для математического ожидания генеральной совокупности.
- •30) Точечные оценки для дисперсии генеральной совокупности.
- •31) Интервальные оценки. Доверительный интервал. Нахождение доверительного интервала для математического ожидания генеральной совокупности с нормальным законом распределения.
- •32) Метод статистической проверки гипотез.
- •33) Распределение основных непрерывных случайных величин.
- •35) Метод фишера. Из "http://www.Wikiznanie.Ru/ru-wz/index.Php/%d0%a1%d1%82%d0%b0%d1%82%d0%b8%d1%81%d1%82%d0%b8%d1%87%d0%b5%d1%81%d0%ba%d0%b8%d0%b9_%d1%80%d1%8f%d0%b4"
Пространство элементарных событй. Случайные события. Алгебра событий.
Под событием в теории вероятности понимается всякий факт, который в результате опыта может произойти или не произойти. Простейшие неразложимые результаты опыта, называются элементарными событиями. Вся совокупность элементарных событий образует пространство элементарных событий. Событие – любое конечное (счетное) подмножество пространства элементарных событий. Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности. Множество σ называется алгеброй событий, если σ множество всех подмножеств множества ω, для которых выполняется следующие условия:
А, В
 σ
σ
 А+В
σ
А+В
σА, В σ А*В σ
А σ
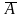 σ
σ
Статистический подход к введению понятия вероятности.Классическое определение вероятности.
Статистическое
определение вероятности.
Пусть производится серия опытов (n),
в результате которых событие А наступает
m
раз число
 - частота наступления события А, тогда
под вероятностью события А будем понимать
предел при Р(А)=
- частота наступления события А, тогда
под вероятностью события А будем понимать
предел при Р(А)=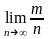
Классическое определение вероятности. Пусть пространство элементарных событий Е состоит из N равновозможных элементарных событий, среди которых имеется n событий, благоприятствующих событию А , тогда число Р ( А ) = n / m называется вероятностью события А .
Теоремы сложения и умножения вероятностей.
Теорема сложения. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий Р(А+В)=Р(А)+Р(В). Предположим, что m случаев благоприятны событию А, а k событию В, тогда Р(А)=m\n; Р(В)=k\n. Так как события А и В несовместны, то нет таких случаев, которые благоприятны А и В вместе. Следовательно, событию А+В благоприятны m+k случаев и Р(А+В)=( m+k)\n
Теорема умножения. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии что первое имело место. Р(АВ)=Р(А)Р(В\А). предположим что событию А благоприятны m случаев, а В – k. Т.к.мы не предполагали события А и В несовместными, то вообще существуют случаи, благоприятные и для А и для В одновременно. Пусть число таких случаев l, тогда Р(АВ)=l\n, Р(А)=m\n. Р(В\А) – условная в-ть события, в предположении что А имело место. Если известно что событие А произошло, то из ранее возможных n случаев остаются возможными только те m,которые благоприятствовали событию А. из них l случаев благоприятны событию В, следовательно Р(А\В)=l\m
Аксиоматическое введение вероятности. Дискретное вероятностное пространство.
Аксиоматическое
определение вероятности.
Пусть задано пространство элементарных
событий Е
и каждому событию А![]() Е
поставлено
в соответствие единственное число Р
(
А ) такое,
что:
Е
поставлено
в соответствие единственное число Р
(
А ) такое,
что:
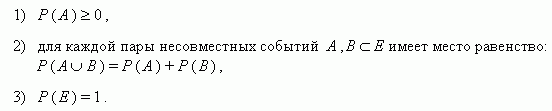
Тогда говорят, что на событиях в множестве Е задана вероятность, а число Р ( А ) называется вероятностью события А .
Формула полной вероятности.
Предположим,
что событие В может произойти с одним
и только с одним из n
несовместных событий А1, А2, …, Аn,
образующих полную группу событий
(Р(А1)+Р(А2)+…+Р(Аn)=1),
т.е. В=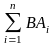 ,
ВАi
и ВАj
несовместны при i≠j
по
т. Сложения Р(В)=
,
ВАi
и ВАj
несовместны при i≠j
по
т. Сложения Р(В)= ,
а по т. умножения Р(В)=
,
а по т. умножения Р(В)=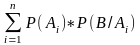 - формула полной вероятности.
- формула полной вероятности.
Формула Байеса.
Пусть произошло событие В; А1, А2, …, Аn – гипотезы. Найдем вероятность гипотезы Р(Аi) при условии, что событие В произошло.
 ;
;
 .
Используя формулу полной вероятности
получим
.
Используя формулу полной вероятности
получим
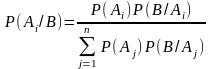 - формула Байеса.
- формула Байеса.
Независимость событий.
События А и В называются независимыми, если Р(АВ) = Р(А) Р(В). Несколько событий А, В, С,… называются независимыми, если вероятность их совместного осуществления равна произведению вероятностей осуществления каждого из них в отдельности: Р(АВС…) = Р(А)Р(В)Р(С)…
Прямое произведение вероятности пространств.
Прямым
произведением пространств исходов
 и
и
 называется
пространство исходов обозначаемое
называется
пространство исходов обозначаемое
 ,
состоящее из упорядоченных пар исходов
,
состоящее из упорядоченных пар исходов
 ,
где
,
где
 ,
,
 .
.
Последовательности независимых испытаний Бернулли. Формула Бернулли.
Пусть
выполняется некоторый эксперимент
(испытание)
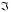 .
В результате этого эксперимента
происходит событие
.
В результате этого эксперимента
происходит событие
 с вероятностью
с вероятностью
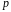 .
Если событие
произошло, то говорят, что результатом
испытания был “успех”
, а в противном случае, говорят, что в
результате испытания имела место
“неудача”.
Вероятность “неудачи”
обозначают
.
Если событие
произошло, то говорят, что результатом
испытания был “успех”
, а в противном случае, говорят, что в
результате испытания имела место
“неудача”.
Вероятность “неудачи”
обозначают
 .
Ясно, что
.
Ясно, что
 .
Казалось бы, это бедная модель, но на
самом деле, она обслуживает большое
число ситуаций. Например, успел – не
успел, выбрали – не выбрали, сдал экзамен
– не сдал экзамен и т.п.
.
Казалось бы, это бедная модель, но на
самом деле, она обслуживает большое
число ситуаций. Например, успел – не
успел, выбрали – не выбрали, сдал экзамен
– не сдал экзамен и т.п.
Если имеются такие условия, что испытание может повторяться неограниченное число раз с неизменной вероятностью “успеха” , причём, исход следующего испытания не зависит от исходов предыдущих испытаний, то говорят, что рассматривается последовательность испытаний Бернулли. Иногда, подчёркивая независимость последовательных испытаний, говорят – последовательность независимых испытаний Бернулли.
