10.Планирование вычислительного эксперимента. Трехфакторный эксперимент.

Для планирования эксперимента необходимо установить критерии оптимизации, которые следует рассчитать в ходе эксперимента, эти критерии как правило должны быть обобщающими но не частными. К обобщающим относят следующие критерии: себестоимость, оборот подвижного состава, пропускная и перерабатывающая способность, приведенные расходы на транспортное обслуживание.

Сначала определяют значение обобщенных критериев при существующем обслуживании, а затем изменяя те или иные параметры входных переменных получают новое значение обобщенных критериев.

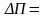П₁-П₂>0 , где

П₁- приведенные расходы при существующем положении

П₂- приведенные расходы при неизменных значениях параметров входной переменной тр-ой сист.

Эффект от изменения структуры тр-ой сист.должен быть положительным, иначе не верно выбраны направления развития и совершенствования путей развития.

Иногда проведение вычислительных экспериментов требует существенных затрат машинного времени и затрат на изготовление моделей функционирования системы.

Требуется меньшим числом экспериментов получить большой объем информации о моделируемой системе. В этих целях применяют теорию планирования эксперимента. Она предлагает различные факторные планы при различном числе варьируемых факторов и при ограниченном числе вычислений экспериментов.

В теории планирования экспериментов фактором считается изменяемый параметр или изменяемая входная переменная(например, в качестве параметра можно принять количество тр-ых ср-в, работающих в тр-ой сист.).

В качестве изменяемых входных параметров учитывают:

• Интервалы поступления тр-ых ср-в в обработку на грузовые пункты и факты, организаций и предприятий

• Количество доставленной партии грузов(массу)

• Коэф.вариаций тр-ого потока по времени и количеству тр-ых ср-в, поступающих в обарботку.

План проведения вычислительного эксперимента при 3 факторах и 8 вычислительных экспериментах. План записывается в таблице:

Номер эксперимента	Х1	Х2	Х3
1	-1	-1	-1
2	1	-1	-1
3	-1	1	-1
4	1	1	-1
5	-1	-1	1
6	1	-1	1
7	-1	1	1
8	1	1	1

1 – max значение изменяемого параметра

(-1) - min значение изменяемого параметра

W стремится к min(max).

ТК-3

1.Разработка моделей функционирования сложных систем. Типы моделей. (данный ответ подходит и для 2го вопроса)

Типы моделей:

-аналитические

-статистические

-графоаналитические

-имитационные.

Для разработки аналитического моделирования сложной системы, применяэт теории. Систем массового обслуживания (СМО).

В теории СМО тр-ые проц.рассматриваэтся как некот.каналы обслуживания, на которые поступают заявки на обслуживание. Заявкой считается поток требований, вязанных с выполнением некоторых интерпритаций(например, каналами обслуживания можно считать: автомобили, грузовые фронты, порт, стнация, АЗС, станция, аэропорт, и т.п.).

СМО применяются при опре.условиях, напрмер, при опред. Количестве каналов обслуживания с учетом закона распределения времени обслуживания. Наиболее общее решение дает для показательного закона распред.времени поступления обслуживания и для показат. закона распред. времени самого обслуживания.

t – интервал поступления заказа

применяя т. СМО можно определить след.выходные переменные рботы тр-го ср-ва:

• Pотк. – вероятность отказа в обслуживании заявки данной системы.

• Nотн. – относительная пропускная способность тр-ой системы показывает какой % заявок, поступающий в систему обслуживания, будет принят.

• r – средняя длина очереди, возникающей в процессе обслуживания.

СМО обычно классифицируют по слуд.признакам:

1. по величине доп.очереди:

• с ограниченной очередью

• с неограниченной очередью

2. по числу каналов обслуживания:

• одноканальные системы

• многоканальные

3. по вероятности отказа в обслуживании заявок:

• системы без отказов

• с внутренними отказами в обслуживании.