1.4.3 Адаптивные фильтры, основанные на методах преобразования сигнала

В другом подходе, обеспечивающем получение импульсов сигнала, близких к прямоугольным, фильтр выполняет умножение в частотной области (рис. 1.8). В гл. 6 описано применение процессоров для адаптивных фильтров, в которых для каждой преобразуемой составляющей сигнала используются отдельные корректирующие контуры. Это обеспечивает также более однородную скорость сходимости по всему фильтру. Показано, что в частотной области фильтрации создает ряд проблем, вследствие применения круговой свертки и групповой обработки данных при дискретном преобразователе Фурье (ДПФ) [40] в сочетании с необходимостью определения используемого типа арифметики: сдвиг – сложение или сдвиг – вычитание. В гл. 6 дан обзор конструкций фильтров, в которых применяется как круговая, так и линейная свертка. Кроме того, описываются [344] адаптивные фильтры, основанные на  преобразованиях Уолша [23]: показано, что в этом случае вычисления упрощаются.

3 Адаптивные алгоритмы для фильтров с конечной импульсной характеристикой

Бенджамин Фридлендер

3.1. Введение

Адаптивные фильтры обычно состоят из двух отдельных частей: фильтра, структура которого рассчитана на выполнение искомой функции обработки информации, и адаптивного алгоритма для подстройки параметров (коэффициентов) этого фильтра. Большое количество возможных комбинаций структур фильтра и законов адаптивного управления ими приводят иногда к поразительному разнообразию адаптивных фильтров.

Яндекс.ДиректВсе объявления Фильтры рукавные СРФ, РФУ Консультации, помощь в подборе оборудования.Фильтры под ключ. td‑ecofilter.ru  Рукавные и картриджные фильтры Двухступенчатые фильтры СРФ10КР для возврата воздуха в цех. Чертежи. Подбор Адрес и телефон efilter.ru 

В данной главе мы сосредоточим внимание на том классе структур фильтров, который, по всей вероятности, является самым простым: на линейных фильтрах с конечной импульсной характеристикой. Типичный фильтр КИХ – типа, реализованный в прямой форме, изображен на рис. 3.1. Отметим, что каждая выборка выходного сигнала фильтра является линейной комбинацией конечного числа предшествующих выборок входного сигнала. Фильтр не является рекурсивным (т. е. не содержит обратной связи);  рекурсивные адаптивные фильтры обсуждаются в гл.4. Отмеченное свойство приводит к исключительно простым адаптивным алгоритмам, как будет показано в последующих разделах.

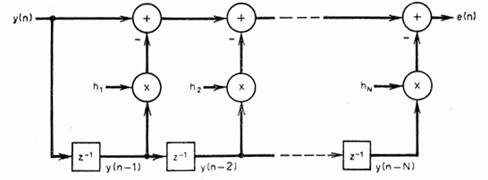
Рис. 3.1. Непосредственная реализация фильтра с конечной импульсной характеристикой.

После определения структуры фильтра возникает необходимость разработки адаптивного алгоритма для подстройки его коэффициентов. В данной главе мы рассматриваем адаптивные законы, цель которых заключается в том, чтобы минимизировать энергию на выходе фильтра (т. е. дисперсию выходного сигнала или выходную сумму квадратов). Необходимость в минимизации этой частной функции стоимости возникает во многих областях применения, включающих оценивание методом наименьших квадратов, например в адаптивном подавлении шума, адаптивном линейном усилении и адаптивном спектральном оценивании. Более детально применения адаптивных фильтров обсуждаются в гл. 8 и 9.

В двух следующих разделах мы даем два адаптивных алгоритма для фильтров КИХ – типа: рекурсивный алгоритм наименьших квадратов (РНК) и алгоритм метода наименьших квадратов (МНК) Уидроу – Хоффа. Алгоритм МНК снискал значительную популярность с начала 1960 –х годов. Его простота делает его привлекательным для многих применений, в которых необходимо минимизировать вычислительные процедуры. Алгоритм РНК широко применяется для идентификации систем и анализа временных рядов. Несмотря на потенциальные преимущества, его применение для обработки сигналов было довольно ограниченным из-за большей вычислительной сложности. В последние годы вновь появился интерес к алгоритму РНК, особенно к его «быстрым» (позволяющим более эффективно проводить расчеты) версиям.

Алгоритм РНК был использован для адаптивной коррекции каналов связи [122, 186, 282], адаптивной обработки сигналов с антенных решеток [232] и других задач.

Вывод алгоритма РНК и краткие сведения о его основных свойствах представлены в разд. 3.2. В гл. 5 алгоритм РНК широко используется в связи с построением решетчатых фильтров, где его называют алгоритмом наименьших квадратов для решетчатых фильтров. В разд. 3.3 мы выводим алгоритм МНК, как аппроксимацию алгоритма РНК, и обсуждаем его свойства и выполняемые преобразования.  И, наконец, в разд. 3.4 мы рассматриваем расчет адаптивного фильтра с заданной структурой. Структура фильтра выбирается такой, чтобы гарантировать линейные фазовые характеристики.