Df 1. Введение в адаптивные фильтры

Питер М. Грант и Колин Ф.Н. Коуэн

1.1. Адаптивная обработка данных

Традиционные системы обработки сигналов, предназначенные для извлечения информации из поступающего сигнала, например, согласованные фильтры, работают по принципу разомкнутого контура, т. е. на данном интервале времени для обработки сигнала используется тот же метод, что и на предшествующем интервале, независимо от результата, полученного на последнем. Иначе говоря, в основу традиционных методов обработки сигнала положено допущение о том, что искажение сигнала является известным и инвариантным во времени.

Адаптивные же устройства обработки сигнала [221, 342] действуют по принципу замкнутого контура (обратной связи). Входной сигнал фильтруется или взвешивается в программируемом фильтре для получения выходного сигнала , который затем сравнивается с полезным, стандартным или обучающим сигналом для нахождения сигнала ошибки . Затем этот сигнал ошибки используется для корректировки весовых параметров процессора (обычно итеративным методом),  с целью постепенной минимизации ошибки (т. е. сигнал на выходе обрабатывающего устройства – процессора - вплотную приближается к величине обучающего сигнала).  Такие процессоры разделяются на два больших класса: адаптивные фильтры (рис. 1.1) и адаптивные антенны [112, 155, 232, 299].

Адаптивные фильтры – тема данной книги: в них используется программируемый фильтр, частотная характеристика или передаточная функция которого изменяется, или адаптируется таким образом, чтобы пропустить без искажения полезные составляющие сигнала и ослабить нежелательные сигналы или помехи, т. е. уменьшить любые искажения входного сигнала. В адаптивных антеннах осуществляется пространственная обработка сигнала с помощью антенной решетки, и на диаграмме создается главный максимум в направлении прихода сигнала и происходит генерация нулей в направлениях источников помех. При этом для подавления помех используются те же методы пространственной обработки сигнала.

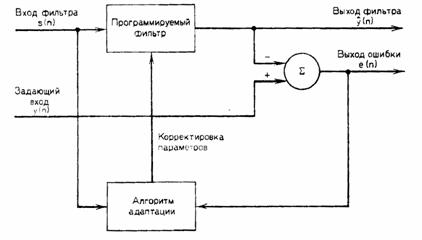
Рис. 1.1 Блок-схема адаптивного фильтра

В адаптивной системе необходим минимальный объем исходной информации о поступающем сигнале. Адаптивный фильтр действует по принципу оценивания статистических параметров поступающего сигнала и подстройки собственной переходной характеристики таким образом, чтобы минимизировать некоторую функцию стоимости. Эту функцию стоимости можно получить рядом способов, в зависимости от предполагаемой области применения, но обычно ее вывод производится с помощью источника второго сигнала на задающем входе, как показано на рис. 1.1. Вторичный входной сигнал можно рассматривать как полезный сигнал на выходе фильтра; задача адаптивного алгоритма – подстройка весов в программируемом фильтрующем устройстве таким образом, чтобы свести к минимуму разность, или ошибку, между сигналами на выходе  и входе фильтра. Такие адаптивные фильтры часто используются для восстановления на выходах каналов сигналов с изменяющимися во времени характеристиками.

Все системы, рассмотренные в данной книге, являются системами обработки импульсных (дискретных по времени) сигналов. Поэтому, для удобства изложения индекс, обозначающий определенный момент времени, исключен из всех математических выражений.