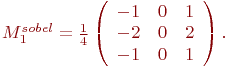Фильтр Гаусса
Фильтр Гаусса относится к числу сглаживающих фильтров. Простейший прямоугольный сглаживающий фильтр - это усреднение.
Основное применений сглаживающих фильтров - шумоподавление. Поскольку шум меняется независимо от пикселя к пикселю, шумы соседних пикселей при суммировании будут компенсировать друг друга. Чем больше окно фильтрации, тем меньше будет усредненная интенсивность шума, однако побочным действием таких фильтров - существенное размытие деталей изображения. Шумоподавление при помощи фильтра усреднения имеет существенный недостаток: все пиксели в маске фильтра на любом расстоянии от обрабатываемой точки оказывают на результат одинаковый эффект. Более эффективное шумоподавление можно осуществить, если влияние пикселей на результат будет уменьшаться с увеличением расстояния. Так устроена гауссовская фильтрация. Матрица фильтра имеет следующий вид:
.
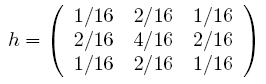http://www.femtoscanonline.com/wiki/ru/processing/фильтр_лапласа
Фильтр Лапласа
Дискретный оператор Лапласа - аналог непрерывного оператора Лапласа. Он эквивалентен последовательному применению градиента и дивергенции. Как иградиент, фильтр Лапласа выделяет границы на изображении.
Вызов фильтра Лапласа осуществляется из меню Математика → Линейные фильтры, преобразование использует матрицу следующего вида:
.
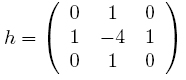Фильтр Собеля задается матрицей
|
http://coderlife.ru/progr/kompternoe-zrenie-operator-sobelya.html
Компьтерное зрение. Оператор Собеля Среда, Февраль 10th, 2010 | Программирование (10 голосов, средний: 4.60 из 5)
Каждый из нас хотя бы раз в жизни встречался с устройством работающим на искусственном интеллекте. Это могли быть: искусственный интеллект компьютерных оппонентов в играх, программы распознавания сканированного текста (например FineReader), фотоаппараты способные распознавать улыбку, программы проводящие опознавание лиц людей на фотографиях, опознание человека по отпечатку пальца и т.д.
Их сейчас очень много! А вы когда-нибудь задумывались над тем как они работают?
Эта очень обширная тема в которой я, как и вы, мало что понимаю.
Одной из первых программ работающих на ИИ (искусственном интеллекте), которую я увидел, была программа сортировки фотографий, основная ее возможность была выбрать все фотографии из папки на которых был запечатлен выбранный человек.
Мне стало жутко интересно как она может это делать? КАК?! Ведь человек может АБСОЛЮТНО произвольно располагаться на фотографии: и вверх ногами, и повернувшись боком или еще как-нибудь – абсолютно не предсказуемо!!! Как вообще найти человека на фотографии??? Чем человек отличается от окружающего мира??? Как на фотографии найти хоть что-нибудь и как его отличить от коробка спичек или от носка?!
Немного порывшись в интернете я набрел на один интересный фильтр для изображений –оператор Собеля.
Он позволяет выделить на изображении границы объектов. Делает он это основываясь на разности яркости объектов. Звучит просто, но кажется, что это сложно реализовать? Абсолютно с вами согласен! Когда я первый раз о нем прочитал я понял что без трех этажных формул тут не обойтись.
ОДНАКО, я был очень удивлен простотой процесса получения этих самых границ, я бы даже сказал крайней простотой!
Итак, как же все-таки получить эти самые границы объектов?
Переводим изображение в оттенки серого
Применяем оператор Собеля к каждому пикселю
В результате работы у нас получиться черно-белое изображение, с яркими границами объектов.
Пример того как работает оператор Собеля
Вообще
сложную теорию вы можете почитать
в википедии.
Я же вам расскажу как, на самом деле, это
просто 
|
|
Итак, будем считать, конвертировать изображение в оттенки серого вы умеете.Если нет, то в конце статьи будет ссылка на мою небольшую демку, в ней вы посмотрите как там происходит «осерение»
Итак, суть алгоритма проста. Результирующий пиксель изображения получается следующем образом:
Находим взвешенную сумму окружающих пикселей, их всего 8 так что бояться нечего Взвешенная сумма – сумма элементов каждый из которых умножен на определенное число. Здесь я немного слукавил, находим две взвешенные суммы , с разным набором множителей, тех самых из определения взвешенной суммы.
Возводим каждую из найденных взвешенных сумм в квадрат, складываем их и сравниваем с числом
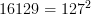(это
если у вас цветовые составляющие пикселя
R, G, B изменяются от 0 .. 255, если же от 0 ..
1, то сравниваете с 
).
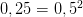Если сумма больше числа, то на
результирующем изображении ставим в
соответствующее место белый пиксель,
иначе черный.
Вот и весь алгоритм! Осталось только показать вам те самые коэффициенты. Вот они:
Коэффициенты оператора Собеля
Они представлены в виде матрицы для наглядности. Коэффициент для текущего пикселя располагается в центре матрицы, для левого верхнего в левом верхнем углу матрицы и т.д.
Итак, вот обещанная программа Sobel. Написана она на C# в Microsoft Visual Studio 2010.
Как пользоваться программой. Запустите Sobel.exe из папки Sobel\bin\Release . Выберите изображение, нажав на левую кнопку, затем нажатием на центральную конвертируйте изображения в оттенки серого и наконец нажатием на правую кнопку примените оператор Собеля.
Гауссово размытие. Нелинейная изотропная диффузия.
http://rsync.altlinux.ru/pub/people/at/gblur.pdf
http://habrahabr.ru/post/151157/