Интерполяционный сплайн

Перевод

ИНТЕРПОЛЯЦИОННЫЙ СПЛАЙН

- сплайн

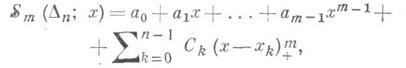
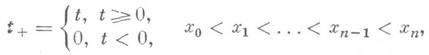
совпадающий с данной функцией в заданных различных точках   Обычно при m=2k+1 полагают   r=0, 1, ..., п, и так как при этом у сплайна   остается еще 2k свободных параметров, то на сплайн налагают еще по кусловий в точках х ₀ и х _п,напр.,  j=1, 2, ..., k, z=x₀, x₁ где  - заданные числа. Если числа   линейно зависят от данной функции, то соответствующий И. с. линейно зависит от этой функции. Для т=2к полагают обычно  =х ₀, =х _п,  i=l, 2, . . ., п-1, и по k условий задают в точках х ₀ и х _п. Если сплайн S_m(A_n, х )в точках х ₁, ..., х _п-х имеет непрерывную (m-s)-ю производную, а (т-s+1)-я производная в них разрывна, то при  в этих точках задают еще производные сплайна от 1-го до (s-1)-го порядка, требуя, чтобы эти производные совпадали с соответствующими производными интерполируемой функции. Рассматриваются также интерполяционные L- и L_q-сплайны и И. с. многих переменйых. И. с. применяются для приближенного представления функций по их значениям на сетке. В отличие от интерполяционных полиномов для И. с. существуют матрицы узлов, для к-рых И. с. сходятся к произвольно заданной непрерывной интерполируемой функции.

3. Линейные операторы обработки изображений. Фильтры Гаусса, Лапласа, Собеля.

Ва http://www.sernam.ru/book_prett1.php?id=8

1.4. Линейные операторы

Яндекс.ДиректВсе объявления Аренда квартир на сутки в Минске! Уютная квартира на сутки в Минске. Быстро, качественно и надёжно! Звоните!!minsknasutki.by Отличный шкаф-купе в Минске у нас Кож. зам., пескоструй, фотопечать, лакомат, ротанг, бамбук, травл-е зеркалоАдрес и телефон panamera.by 

Двумерная система называется линейной, если для нее справедлив принцип суперпозиции. В частном случае отображения функции в функцию для этого требуется, чтобы

         (1.4.1)

где   — некоторые постоянные (могут быть комплексными). Определение свойства суперпозиции можно легко распространить на отображение (1.2.1) общего вида.

Используя свойство дельта-функции (1.3.1г), функцию на входе системы   можно представить как взвешенную сумму дельта-функций:

                        (1.4.2)

где   — весовой множитель дельта импульса, имеющего координаты   на плоскости   (рис. 1.4.1). Если функция на выходе линейной системы

                                              (1.4.3)

то

    (1.4.4а)

или

   (1.4.4б)

Для перехода от выражения (1.4.4а) к (1.4.4б) был изменен порядок выполнения операций линейного преобразования и интегрирования. Линейный оператор действовал только на тот множитель подынтегрального выражении (1.1.4а), который зависит от пространственных переменных  . Запишем второй множитель подынтегрального выражения (1.4.4б) как

              (1.4.5)

Будем называть эту функцию импульсным откликом двумерной системы. Импульсный отклик оптической системы часто называется функцией рассеяния точки.

Рис. 1.4.1. Представление функции, описывающей изображение, в виде суперпозиции дельта-функций.

Подстановка импульсного отклика в соотношение (1.4.4б) дает интеграл суперпозиции

               (1.4.6)

Линейная двумерная система называется пространственно-инвариантной (изопланатической), если ее импульсный отклик зависит только от разностей координат  . Для оптической системы, показанной на рис. 1.4.2. это значит, что при перемещении точечного источника в предметной плоскости изображение этого источника в плоскости фокусировки будет также изменять положение, но сохранять форму. Для пространственно-инвариантной системы

                                (1.4.7)

и интеграл суперпозиции имеет особую форму, называемую интегралом свертки:

       (1.4.8а)

Операции свертки символически записывается как

                                                (1.4.8б)

Интеграл свертки симметричен, т. е.

         (1.4.9)

Процесс свертки иллюстрируется на рис. 1.4.3. На рис. 1.4.3, а и 1.4.3, б изображены функция   на входе и импульсный отклик.

Рис. 1.4.2. Изображение точечного источника света в оптической системе.

На рис.1.4.3, в показан импульсный: отклик при обращении координат, а на рис. 1.4.3, г — со сдвигом на величину  . На рис. 1.4.3, д заштрихована область, в которой произведение  , входящее в подынтегральное выражение (1.4.8, а), не равно нулю. Интегрирование на этой области дает величину   для заданных значений координат  . Таким образом, функция   на выходе может быть найдена сканированием входной функции скользящим «окном» — обращенным импульсным откликом, и интегрированием по области, в которой эти функции перекрываются.

Рис. 1.4.3. Пример двумерной свертки.

Pre#tt U. Cifrovaja obrabotka izobrazhenij, tom 1 с. 205

http://rsync.altlinux.ru/pub/people/at/gblur.pdf

http://www.femtoscanonline.com/wiki/ru/processing/%D1%84%D0%B8%D0%BB%D1%8C%D1%82%D1%80_%D0%B3%D0%B0%D1%83%D1%81%D1%81%D0%B0