[Править]Способы интерполяции [править]Интерполяция методом ближайшего соседа
Простейшим способом интерполяции является интерполяция методом ближайшего соседа.
[Править]Интерполяция многочленами
На практике чаще всего применяют интерполяцию многочленами. Это связано прежде всего с тем, что многочлены легко вычислять, легко аналитически находить их производные и множество многочленов плотно в пространстве непрерывных функций (теорема Вейерштрасса).
Линейная интерполяция
Интерполяционная формула Ньютона
Метод конечных разностей
ИМН-1 и ИМН-2
Многочлен Лагранжа (интерполяционный многочлен)
По схеме Эйткена
Сплайн-функция
Кубический сплайн
[править]Обратное интерполирование (вычисление x при заданном y)
Полином Лагранжа
Обратное интерполирование по формуле Ньютона
Обратное интерполирование по формуле Гаусса
[править]Интерполяция функции нескольких переменных
Билинейная интерполяция
Бикубическая интерполяция
[править]Другие способы интерполяции
Рациональная интерполяция
Тригонометрическая интерполяция
Сплайн
[править]
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 декабря 2012; проверки требует 1 правка.
Сплайн (от англ. spline, от [flat] spline — гибкое лекало, полоса металла, используемая для черчения кривых линий) — функция, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом. Максимальная степень из использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна. Например, непрерывная ломаная есть сплайн степени 1 и дефекта 1.
Сплайны имеют многочисленные применения как в математической теории, так и в разнообразных вычислительных приложениях. В частности, сплайны двух переменных интенсивно используются для задания поверхностей в различных системах компьютерного моделирования.
Содержание [убрать]
|
[Править]Определение и история
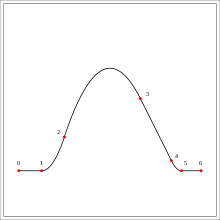
Квадратичный сплайн из шести полиномиальных сегментов. Между точками 0 и 1 — прямая линия. Между точками 1 и 2 — парабола со второй производной, равной 4. Между точками 2 и 3 — парабола со второй производной, равной −2. Между точками 3 и 4 прямая линия. Между точками 4 и 5 — парабола со второй производной, равной 6. Между точками 5 и 6 прямая линия.
Кубический сплайн, составленный из семи полиномиальных сегментов.
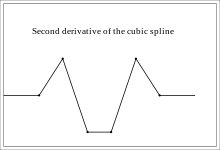
Вторая производная кубического сплайна на рисунке выше.
Сплайном (spline) называли гибкую металлическую линейку — универсальное лекало[1], которое использовали чертежники для того, чтобы гладко соединить отдельные точки на чертеже, то есть для графического исполнения интерполяции. Более того, кривая, описывающая деформацию гибкой линейки, зафиксированной в отдельных точках, является сплайном. Итак, имеется физическая модель сплайн-функции (или, наоборот, сплайн-функция является математической моделью гибкой линейки). Интуитивный подход к использованию кусочных функций в задачах аппроксимации встречался в математике в течение длительного времени. Но, как отмечает советский учёный Николай Корнейчук, вторжение сплайнов в теорию приближения произошло из-за задачи интерполяции, благодаря их хорошим вычислительным и аппроксимативным свойствам.
Теория интерполяции сплайнами и сам термин сплайн ведут свой отсчёт со статьи Айзека Шонберга (англ. Isaac Jacob Schoenberg) 1946 года. Особенно интенсивное её развитие произошло в 50-70 годы, традиционной прикладной сферой использования интерполяционных сплайнов стали в настоящее время системы автоматизированного проектирования. Однако потенциальные возможности сплайнов значительно шире, чем просто описание некоторых кривых. В реальном мире большое количество физических процессов по самой своей природе являются сплайнами. В механике это деформация гибкой пластины или стержня, зафиксированных в отдельных точках; траектория движения тела, если сила, действующая на него меняется ступенчато (траектория искусственного космического объекта с активными и инерционными отрезками движения, траектория движения самолета при ступенчатом изменении тяги двигателей и изменении профиля крыла и т. д.). В термодинамике это теплообмен в стержне, составленном из фрагментов с различной теплопередачей. В химии — диффузия через слои различных веществ. В электричестве — распространение электромагнитных полей через разнородные среды. То есть сплайн не выдуманная математическая абстракция, а во многих случаях он является решением дифференциальных уравнений, описывающих вполне реальные физические процессы.
Рассмотрение
сплайнов начнем с определения
алгебраического сплайна []:
Функция 
определенная
и непрерывная на отрезке 
,
называется полиномиальным
сплайном порядка 
с
узлами 
,
если на каждом из отрезков 
,
является
алгебраическим полиномом степени, не
превышающей
,
а в каждой из точек 
некоторая
производная 
может
иметь разрыв. Если в точке
непрерывные
функции 
,
а производная 
в
точке
терпит
разрыв, число называют дефектом
сплайна.
Множество 
называют
сеткой узлов сплайна, а точки
узлами
или точками соприкосновения или склейки
сплайна.
Как
следует из определения, для построения
сплайна, состоящего из 
фрагментов,
требуется найти такие значения числовых
параметров для каждого фрагмента —
полинома степени
,
которые обеспечат непрерывность в узлах
как самой функции, так и необходимых
производных. Так, всего следует
определить 
параметров.
С учетом условия интерполяции и
непрерывности первых двух производных
определение параметров сводится к
решению системы с 
линейных
уравнений. Как правило, значения
коэффициентов для отрезков полиномов
непосредственно не рассчитываются.
Для определения интерполяционного сплайна с непрерывной первой производной, достаточно рассчитать значение первой производной в узлах. Способ определения производных в узлах сплайна определяет широкое разнообразие интерполяционных сплайнов. Часто производные определяются не как константы, а как некоторые зависимости от интерполируемой функции и сетки интерполяции.
Если значение первой производной в узлах рассчитывать исходя из условия непрерывности второй производной (решая систему с n линейных уравнений), то сплайн будет иметь две непрерывные производные. Такой способ построения сплайна, как и сам сплайн называют глобальным, поскольку при определении каждого из его коэффициентов учитывается все множество узлов интерполяции.
В других случаях, для определения отдельного коэффициента учитываются только ближайшие узлы интерполяции и такие способы построения, как и сами сплайны, называют локальными. Параметры фрагмента такого сплайна можно определить независимо от других фрагментов.
Простым условием построения фрагмента локального сплайна является условие равенства полинома на концах отрезков соответствующим значениям интерполируемой функции.
Для простейшего сплайна — ломаной — этого условия вполне достаточно. Два коэффициента прямой однозначно определяются из двух уравнений. Такой сплайн является локальным. Для полиномов высших степеней мы должны добавить дополнительные условия таким образом, чтобы общее число уравнений было равно числу коэффициентов полинома. Так, для сплайна 3-й степени таким условием является равенство 1-й производной на концах отрезка некоторому значению, которое определяется для соседних участков одинаковым образом (в формулах (2) через значение производной функции, которой приближают).
Система из 4-х уравнений
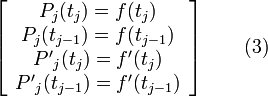
позволяет однозначно определить 4 коэффициента полинома. Для полинома 5-й степени мы должны дополнительно наложить условие равенства 2-й производной на концах отрезка и т. д. Приведенное выше показывает, почему сплайны строят преимущественно из полиномов нечётных степеней (с чётным количеством коэффициентов).
Для полиномов четных степеней при сборке системы (3) остается неопределенной производная в одном из концов отрезка, и условие равенства производных (гладкости кривой) не будет выполняться. Поэтому для полинома 2-й степени невозможно достичь равенства первой производной в точках стыка, а для 4-й степени — второй производной и т. д., исходя из системы уравнений (3). Для построения сплайнов с четными степенями искусственно добавляют дополнительные условия чтобы сформировать систему уравнений, подобную (3). Когда производные полинома сплайна определяются как соответствующие производные интерполируемой функции, то сплайн является эрмитовым.
Существуют локальные методы построения сплайнов Бесселя и Акими, B — сплайны []. В основном, когда речь идет о сплайнах, то имеют в виду сплайны, построенные из алгебраических полиномов. Именно к ним относится приведенное выше определение. Именно эти сплайны являются наиболее изученными. Однако сплайн может состоять из фрагментов функций любого класса. В [] рассмотрено построение таких сплайнов и исследуются их свойства. Автор не дает общего определения построенных сплайнов. Очевидно, что для любых классов функций, из которых состоит сплайн, приведенное в начале статьи определение не совсем подходит. Если, например, сплайн состоит из отрезков экспоненты, то понятие дефекта сплайна теряет смысл. Хотя количество непрерывных производных останется важной характеристикой. Построение сплайна, фрагментами которого являются разрывные функции (рациональные функции, функции Паде), несколько выходит за рамки сплайновой идеи, поскольку одним из основных преимуществ сплайнов является их гладкость. Если произвольно расширять такие конструкции, то стираются различия сплайнов от кусковых функций. Другим преимуществом сплайнов является эффективность вычислений. Чрезмерное усложнение фрагментов существенно снижает преимущество сплайнов перед классическими функциями.
Для сплайнов характерны следующие признаки: сплайн состоит из фрагментов — функций одного класса, которые отличаются только своими параметрами, на соседние фрагменты в точках стыковки накладываются определенные условия, которые сводятся к непрерывности значений и некоторых первых производных. Сплайны — направление прикладной математики, которое интенсивно развивается. В Интернете содержится обширная библиография по сплайнов (Spline Bibliography Database (SBD)) .