8.4. Сглаживание данных

Сглаживание данных, как искаженных помехами, так и статистических по своей природе, также можно считать частным случаем регрессии без определения символьной формы ее функции, а потому может выполняться более простыми методами. Обычно для сглаживания применяются линейное сглаживание методом наименьших квадратов по k ближайших отсчетов с адаптивным выбором значения k; сглаживание данных на основе распределения Гаусса; сглаживание данных по методу скользящей медианы и др.

Сопоставление методов сглаживания приведено на рис. 8.4.1. Как можно видеть на этом рисунке, качество сглаживания двух первых методов примерно одинаково. Медианный способ уступает по своим возможностям двум другим. Особенно на концах интервала задания данных.

Рис. 8.4.1

8.5. Предсказание зависимостей

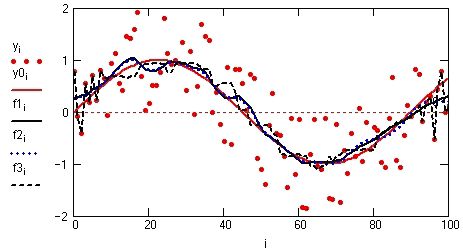
По вектору равномерно распределенных данных Y, иногда требуется составить вектор К точек предсказания (экстраполяции) поведения произвольного сигнала за пределами его задания (по возрастанию координат х). Предсказание тем точнее, чем более гладкую форму имеет заданный сигнал. Пример предсказания для гладкой аналитически заданной функции f₁(x) и статистически зашумленных экспериментальных данных f₂(x) приведен на рис. 8.5.1. Степень аппроксимирующего полинома определяет глубину использования входных данных и может быть достаточно небольшой для гладких и монотонных сигналов. Ошибка прогнозирования увеличивается по мере удаления от заданных данных.

Рис. 8.5.1

3. Параболическая и экспоненциальная регрессия.

http://dic.academic.ru/dic.nsf/enc_mathematics/3832/%D0%9F%D0%90%D0%A0%D0%90%D0%91%D0%9E%D0%9B%D0%98%D0%A7%D0%95%D0%A1%D0%9A%D0%90%D0%AF

Аппроксимация. Параболическая регрессия

В общем случае при описании функциональной зависимости между двумя случайными величинами используют полиномы некоторой степени, коэффициенты которых могут и не иметь определенного физического смысла. Такая операция называется аппроксимацией экспериментальных данных. Полученная эмпирическая формула обычно справедлива только для сравнительно узкого интервала измерений и неприменима вне этого интервала. При использовании метода наименьших квадратов коэффициенты приближенного уравнения регрессии определяются решением системы линейных уравнений.

Допустим, что зависимость между величинами Х и Y описывается параболой второго порядка

        .        (8.32)

Тогда

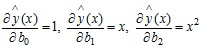        ,        (8.33)

И система нормальных уравнений (7.43) принимает вид

        ,

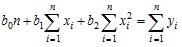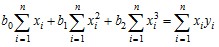        ,        (8.34)

        .

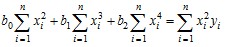Решая систему (8.34), находят коэффициенты искомой квадратичной функции. При описании функциональных зависимостей полиномами большей степени коэффициенты определяются из аналогичных по структуре систем уравнений.

На практике адекватности уравнения регрессии эксперименту добиваются повышением степени аппроксимирующего полинома. При использовании полинома kстепени требуется определять k + 1 коэффициент. Увеличение степени полинома прекращают, если дисперсия адекватности (остаточная дисперсия) уравнения регрессии k + 1 степени ( ) перестает быть значимо меньше дисперсии адекватности, вычисленной для полинома k-степени ( ). Значимость различия исследуется по критерию Фишера

        ,

Где

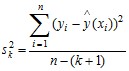        ,  .        (8.35)

Если полученное F меньше табличного F1-p(f1, f2) для уровня значимости р и чисел степеней свободы f1 = f k = n – k – 1 и f2 = f k+1 = n – k – 2, то увеличение степени полинома нужно прекратить и в качестве приближенного уравнения регрессии использовать полином k-степени.

экспоненциальная 

3. Алгоритм Чайкина. Быстрое вейвлет-преобразование.

http://sergeshibaev.ru/programmer-notes/10-fwtsharc

Df Вейвлет-преобразование в последнее время находит все большее применение в цифровой обработке сигналов. С его помощью проводится сжатие, очистка от шумов, подчеркивание особенностей сигнала и т. д. Тем не менее, несмотря на уже доказанную необходимость в подобных вычислениях, программное обеспечение современных цифровых сигнальных процессоров не содержит, наряду с преобразованием Фурье, библиотеку вейвлет-преобразования. Причиной этого может быть большое количество вычислений, а, следовательно, и времени, необходимого для выполнения непрерывного вейвлет-преобразования. Другой возможной причиной может являться пока еще недостаточная популярность подобных методов обработки. Однако, как показывают многие работы по вейвлет-анализу, число вычислений можно заметно сократить.

В частности, из теории кратномасштабного анализа широко известны формулы так называемого "быстрого вейвлет-преобразования", которые удобно представить в матричном виде (1):

Формула (1) представляет собой один шаг вейвлет-преобразования, в результате чего входной сигнал x_i длиной N делится на две составляющие - y_i и z_i, состоящих из N/2 элементов. На каждом последующем шаге преобразованию будет подвергаться верхняя половина нового вектора. Число шагов зависит от конкретной задачи, и преобразование может продолжаться до тех пор, пока длина вектора входного сигнала больше или равна длине последовательностей h и g.

Формулу (1) можно представить как свертку последовательностей

y_i = x_i * h_i,

z_i = x_i * g_i

с последующей децимацией в 2 раза.В такой постановке последовательности h и g принято называть фильтрами. Фильтр h используется для выделения приближенной (низкочастотной) части сигнала, а фильтр g – для выделения детализирующей (высокочастотной) информации. Заметим, что в этих формулах нигде в явном виде не используются ни вейвлеты, ни масштабирующие функции, их роль играют фильтры h и g, элементами которых являются коэффициенты соответствующих масштабных соотношений. Есть целое семейство ортогональных вейвлетов, которые вообще не имеют аналитического выражения и определяются только фильтрами. Это семейство носит название вейвлетов Добеши. Таким образом, вейвлет-преобразование сигнала сводится к фильтрации сигнала НЧ и ВЧ фильтрами. С вычислительной точки зрения операция свертки содержит в себе циклически повторяющиеся операции умножения/накопления в сочетании с чтением данных и записью результатов, то есть работой с оперативной памятью. Кроме того, для выполнения этой процедуры в реальном времени, необходимо продолжать поступление сигнала на вход вычислительной системы.

http://emf.ipgg.nsc.ru/mpg/geoinformatics/abstracts/sim_2.pdf

алгоритм чайкина

http://gendocs.ru/docs/28/27659/conv_6/file6.pdf

3. Интерполяция данных. Аппроксимационные и интерполяционные сплайны.

Ва http://www.polybook.ru/comma/1.3.pdf

http://itmu.vsuet.ru/Posobija/MathCAD/gl14/index.htm