- •Раздел I. Линейные системы. Цифровые фильтры
- •Системы хранения медиаданных
- •Скорости и интерфейсы
- •Расчет аналогового нормированного фильтра нижних частот Баттерворта
- •Df 1. Введение в адаптивные фильтры
- •1.1. Адаптивная обработка данных
- •1.1.1 Адаптивные фильтры
- •1.1.2 Принцип действия адаптивного фильтра
- •1.4 Адаптивные фильтры
- •1.4.1 Адаптивные фильтры с бесконечной импульсной характеристикой
- •1.4.2 Адаптивные фильтры с конечной импульсной характеристикой
- •1.4.3 Адаптивные фильтры, основанные на методах преобразования сигнала
- •3 Адаптивные алгоритмы для фильтров с конечной импульсной характеристикой
- •3.1. Введение
- •4. Адаптивные алгоритмы для фильтров с бесконечной импульсной характеристикой
- •4.1. Введение
- •4.1.1 Общий обзор
- •2.3 Оптимальное рекурсивное калмановское оценивание
- •2.3.1 Скалярный фильтр Калмана
- •2.3.2. Вывод коэффициента фильтра Калмана
- •2.4. Векторный фильтр Калмана
- •2.4.1. Векторный фильтр Калмана в качестве устройства коррекции канала
- •Требования к вейвлетам
- •Свойства вейвлет преобразования
- •Непрерывное вейвлет-преобразование
- •Дискретное вейвлет-преобразование
- •Графическое представление
- •Применение
- •Примечания
- •Чирплет
- •Аналогия с другими преобразованиями
- •Чирплеты и чирплет-преобразование
- •Приложения
- •Систематика чирплет-преобразования
- •Df Глава 1. Постановка задачи и обзор моделей прогнозирования временных рядов
- •1.1. Содержательная постановка задачи
- •1.2. Формальная постановка задачи
- •1.3. Обзор моделей прогнозирования
- •1.3.1. Регрессионные модели
- •1.3.2. Авторегрессионные модели
- •1.3.3. Модели экспоненциального сглаживания
- •1.3.4. Нейросетевые модели
- •1.3.5. Модели на базе цепей Маркова
- •1.3.6. Модели на базе классификационно-регрессионных деревьев
- •1.1.1. Другие модели и методы прогнозирования
- •1.4. Сравнение моделей прогнозирования
- •1.4.1. Достоинства и недостатки моделей
- •1.4.2. Комбинированные модели
- •1.5. Выводы
- •Тема 15. Регрессия
- •Введение
- •15.1. Постановка задачи регрессии
- •15.2. Линейная регрессия [25]
- •15.3. Полиномиальная регрессия [25]
- •15.4. Нелинейная регрессия [25]
- •15.5. Сглаживание данных [25]
- •15.6. Предсказание зависимостей [25]
- •Df Линейная регрессия
- •8. Регрессия
- •8.1. Детерминированные и статистические зависимости
- •8.2. Корреляция и коэффициент корреляции
- •8.3. Уравнения регрессии
- •8.3.1. Линейная регрессия
- •8.3.2. Полиномиальная регрессия
- •8.3.3. Нелинейная регрессия
- •8.4. Сглаживание данных
- •8.5. Предсказание зависимостей
- •Параболическая и экспоненциальная регрессия.
- •Аппроксимация. Параболическая регрессия
- •Интерполяция
- •[Править]Определения
- •[Править]Пример
- •[Править]Способы интерполяции [править]Интерполяция методом ближайшего соседа
- •[Править]Интерполяция многочленами
- •[Править]Определение и история
- •[Править]Классификация сплайнов
- •Интерполяционный сплайн
- •1.4. Линейные операторы
- •Фильтр Гаусса
- •Фильтр Лапласа
- •Компьтерное зрение. Оператор Собеля Среда, Февраль 10th, 2010 | Программирование (10 голосов, средний: 4.60 из 5)
- •Быстрое размытие по Гауссу
Расчет аналогового нормированного фильтра нижних частот Баттерворта
Содержание
Введение. Исходные данные для расчета фильтра Баттерворта. Основные соотношения при аппроксимации АЧХ фильтра
Порядок расчета фильтра Баттерворта
Нули и полюса фильтра Баттерворта
Расчет передаточной характеристики фильтра Баттерворта
Пример расчета фильтра Баттерворта
Выводы
Введение. Исходные данные для расчета фильтра Баттерворта. Основные соотношения при аппроксимации АЧХ фильтра
В предыдущей статье мы рассмотрели основные свойства полиномов комплексной переменной и передаточной функции аналогового фильтра . Также была рассмотрена постановка задачи расчета фильтра, и проанализированы основные виды аппроксимирующих полиномов АЧХ фильтра.
В данной статье мы рассмотрим расчет фильтра Баттерворта по заданному коридору АЧХ, показанному на рисунке 1.
Рисунок 1: Идеальная и реальная АЧХ ФНЧ
Приведем основные соотношения связывающие параметры аппроксимации АЧХ (данные соотношения были подробно рассмотрены здесь):
|
(1) |
Аппроксимация АЧХ ФНЧ Баттерворта представляется в виде:
|
(2) |
Порядок фильтра Баттерворта рассчитывается из уравнения:
|
(3) |
Прологарифмируем правую и левую части уравнения и получим:
|
(4) |
Все вышеприведенные соотношения уже были рассмотрены ранее. Мы привели их еще раз без пояснений, и они нам будут необходимы при рассечет фильтра Баттерворта.
Порядок расчета фильтра Баттерворта
Итак приступим. Исходными данными для расчета фильтра Баттерворта служат: частота среза , переходная полоса, задаваемая , допустимое искажение в полосе пропускания и требуемое подавление в полосе заграждения .
Первый шаг: из выражения (1) рассчитываются параметры , , и .
Второй шаг расчет требуемого порядка фильтра согласно выражению (4).
Третий
шаг расчет передаточной функции
фильтра ![]() .
Здесь мы остановимся подробнее.
.
Здесь мы остановимся подробнее.
Нули и полюса фильтра Баттерворта
Для
расчета нулей и полюсов подставим в
выражение аппроксимации АЧХ (2) ![]() ,
тогда
,
тогда
|
(5) |
Очевидно,
что ни при каких конечных
комплексных ![]() выражение
(5) не равно нулю, другими словами, фильтр
Баттерворта не имеет нулей. Для расчета
полюсов фильтра Баттерворта приравняем
знаменатель к нулю:
выражение
(5) не равно нулю, другими словами, фильтр
Баттерворта не имеет нулей. Для расчета
полюсов фильтра Баттерворта приравняем
знаменатель к нулю:
|
(6) |
Рассмотрим отдельно четные и нечетные . При четных имеем:
|
(7) |
Представим ![]() в
правой части через комплексную
экспоненту
в
правой части через комплексную
экспоненту ![]() ,
,![]() ,
тогда
,
тогда
|
(8) |
Прологарифмируем левую и правую части уравнения получим:
|
(9) |
Преобразуем:
|
(10) |
тогда:
|
(11) |
И окончательно можно записать выражения для полюсов передаточной функции при четных :
|
(12) |
При нечетных из выражения (6) имеем:
|
(13) |
Представим ![]() в
правой части через комплексную
экспоненту
в
правой части через комплексную
экспоненту ![]() ,
,
тогда
,
,
тогда
|
(14) |
Прологарифмируем левую и правую части уравнения получим:
|
(15) |
Преобразуем:
|
(16) |
тогда:
|
(17) |
И окончательно можно записать выражения для полюсов передаточной функции при нечетных :
|
(18) |
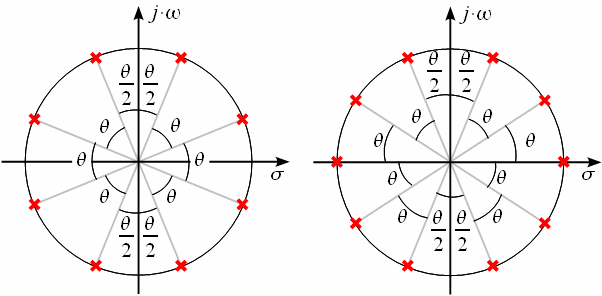
На
рисунке 2 показаны расположения полюсов
квадрата модуля передаточной функции,
заданной выражением (5) при четном
(слева)и
нечетном ![]() (справа)
порядках фильтра Баттерворта.
(справа)
порядках фильтра Баттерворта.
 Рисунок
2: Расположение полюсов квадрата модуля
передаточной функции при четном
и
нечетном
порядках
фильтра Баттерворта
Рисунок
2: Расположение полюсов квадрата модуля
передаточной функции при четном
и
нечетном
порядках
фильтра Баттерворта
Все
полюса квадрата модуля АЧХ фильтра
Баттерворта расположены на окружности
радиуса ![]() ,
и отстоят друг от друга на угол
,
и отстоят друг от друга на угол ![]() .
При
все
полюса расположены на единичной
окружности.
.
При
все
полюса расположены на единичной
окружности.
Расчет передаточной характеристики фильтра Баттерворта
Ранее говорилось, что для получения устойчивого и физически реализуемого фильтра необходимо, чтобы все нули и полюса располагались в левой полуплоскости комплексной плоскости. Тогда для расчета передаточной функции фильтра Баттерворта необходимо из всех полюсов выбрать только те, что лежат в левой полуплоскости. Тогда все полюса расположенные в левой полуплоскости могут быть записаны как для четного , так и для нечетного (смотри рисунок 2):
|
(19) |
Или перепишем в тригонометрической форме:
|
(20) |
Таким образом мы задали все полюса передаточной функции фильтра Баттерворта порядка . Тогда передаточная функция фильтра Баттерворта может быть представлена :
|
(21) |
Обратим внимание, что все полюса передаточной функции фильтра Баттерворта четного порядка (смотри рисунок 2) представляют собой комплексно-сопряженные пары, а у фильтра нечетного порядка есть один вещественный полюс. Тогда можно представить передаточную функцию фильтра Баттерворта при помощи биквадратной формы. Для четного :
|
(22) |
Тогда окончательно можно записать:
|
(23) |
В
случае нечетного
имеем
дополнительный вещественный полюс ![]() .
Тогда для нечетного
можно
представить передаточную функцию
фильтра Баттерворта при помощи
биквадратной формы как:
.
Тогда для нечетного
можно
представить передаточную функцию
фильтра Баттерворта при помощи
биквадратной формы как:
|
(24) |
Окончательно
можно объединить выражения (23) и (24). Для
любого целого![]() (
(![]() может
принимать значения 0 или 1) передаточную
функцию фильтра Баттерворта можно
представить в виде:
может
принимать значения 0 или 1) передаточную
функцию фильтра Баттерворта можно
представить в виде:
|
(25) |
Коэффициент
передачи фильтра Баттерворта на нулевой
частоте ![]() равен:
равен:
|
(26) |
Для
нормировки коэффициента передачи
фильтра Баттерворта на нулевой
частоте ![]() необходимо
передаточную функцию фильтра Баттерворта
(25) разделить на
.
Тогда получим характеристику нормированного
ФНЧ Баттерворта в виде:
необходимо
передаточную функцию фильтра Баттерворта
(25) разделить на
.
Тогда получим характеристику нормированного
ФНЧ Баттерворта в виде:
|
(27) |
Необходимо
отметить, что при
, ![]() и
без
нормировки, при этом
соответствует
и
без
нормировки, при этом
соответствует![]() .
При этом выражение для передаточной
характеристики фильтра (27) преобразуется
к виду:
.
При этом выражение для передаточной
характеристики фильтра (27) преобразуется
к виду:
|
(28) |
Такая форма записи (28) передаточной характеристики получила широкое распространение ввиду того, что не требуется нормировки. Однако выражение (27) позволяет регулировать коэффициент передачи фильтра на частоте среза и является более общей.
Пример расчета фильтра Баттерворта
Рассчитаем нормированный ФНЧ Баттерворта при следующих параметрах коридора АЧХ:
|
(29) |
Шаг 1
Рассчитываем все необходимые параметры исходя из выражения (1):
|
(30) |
Шаг 2
Рассчитываем порядок фильтра согласно выражению (4):
|
(31) |
Округляем
до ближайшего целого в большую сторону,
получаем, что заданному коридору
удовлетворяет ![]() .
.
Шаг 3
Рассчитываем передаточную характеристику согласно выражению (27).
При
этом ![]() значит
значит ![]() ,
, ![]() .
Рассчитываем
.
Рассчитываем ![]()
|
(32) |
Рассчитываем
значения ![]() .
В нашем случае
,
поэтому будет только одно значение
.
В нашем случае
,
поэтому будет только одно значение ![]() равное
:
равное
:
|
(33) |
Тогда передаточную характеристику фильтра можно записать:
|
(34) |
На этом расчет фильтра Баттерворта окончен
Комплексный коэффициент передачи полученного фильтра равен:
|
(35) |
На
рисунках 3 - 5 показаны АЧХ
,
ФЧХ ![]() и
групповая задержка
и
групповая задержка ![]() рассчитанного
фильтра Баттерворта третьего порядка.
рассчитанного
фильтра Баттерворта третьего порядка.
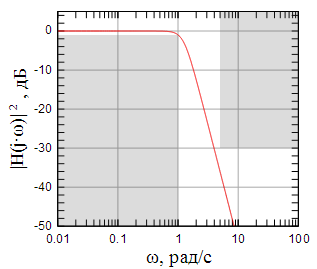
Р |
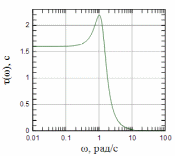
Рисунок 4: ФЧХ рассчитанного фильтра Баттерворта |
Рисунок 5: Групповая задержка рассчитанного фильтра Баттерв орта |
На графике АЧХ (рисунок 3) серым отмечен заданный коридор АЧХ. Обратите внимание, что по оси абсцисс частота представлена в логарифмическом масштабе. Видно что полученная АЧХ помещается в коридор даже с запасом, так как при расчете использовался порядок равный 3 вместо 2.56545 (дробный порядок не может быть).
Отметим, что на практике для программной реализации функции расчета передаточной функции необходимо численно перемножать полиномы при помощи линейной свертки. Подробно данный вопрос был рассмотрен здесь.
Выводы
Таким образом, в данной статье мы рассмотрели порядок расчета передаточной функции аналогового ФНЧ Баттерворта и привели пример расчета фильтра по заданному коридору АЧХ.
Расчет аналогового эллиптического фильтра нижних частот
Содержание
Введение. Исходные данные и основные соотношения при аппроксимации АЧХ фильтра
Порядок расчета эллиптического фильтра
Нули и полюса эллиптического фильтра
Передаточная характеристика эллиптического фильтра
Пример расчета эллиптического фильтра
Выводы
Введение. Исходные данные и основные соотношения при аппроксимации АЧХ фильтра
В предыдущей
статье мы
рассмотрели основные свойства полиномов
комплексной переменной и передаточной
функции аналогового фильтра ![]() .
Также была рассмотрена постановка
задачи расчета
фильтра, и проанализированы основные
виды аппроксимирующих полиномов АЧХ
фильтра.
.
Также была рассмотрена постановка
задачи расчета
фильтра, и проанализированы основные
виды аппроксимирующих полиномов АЧХ
фильтра.
В данной статье мы рассмотрим расчет нормированного эллиптического фильтра Кауэра (Золотарева-Кауэра) по заданному коридору АЧХ, показанному на рисунке 1.
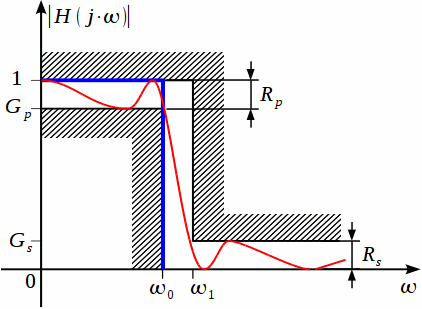 Рисунок
1: Идеальная и реальная АЧХ ФНЧ
Рисунок
1: Идеальная и реальная АЧХ ФНЧ
В отличии от фильтров Чебышева первого и второго рода, АЧХ эллиптических фильтров имеет равноволновые колебания как в полосе пропускания, так и в полосе заграждения.
Приведем основные соотношения связывающие параметры аппроксимации АЧХ (данные соотношения были подробно рассмотрены здесь):
|
(1) |
Аппроксимация АЧХ нормированного ФНЧ Кауэра представляется в виде:
|
(2) |
где ![]() - эллиптическая
дробно-рациональная функция,
зависящая от параметра
- эллиптическая
дробно-рациональная функция,
зависящая от параметра ![]() порядка
порядка ![]() :
:
|
(3) |
Все вышеприведенные соотношения уже были рассмотрены ранее. Мы привели их еще раз без пояснений, и они нам будут необходимы при рассечете фильтра Кауэра.
Порядок эллиптического фильтра можно рассчитать из уравнения:
|
(4) |
где ![]() -
полный эллиптический интеграл, а
-
полный эллиптический интеграл, а ![]() -
полный комплиментарный эллиптический
интеграл (подробнеездесь),
а
и
-
полный комплиментарный эллиптический
интеграл (подробнеездесь),
а
и ![]() рассчитываются
согласно (1).
рассчитываются
согласно (1).
Порядок расчета эллиптического фильтра Кауэра
Итак
приступим. Исходными данными для расчета
эллиптического фильтра служат: частота
среза ![]() ,
переходная полоса, задаваемая
,
переходная полоса, задаваемая ![]() ,
допустимое искажение в полосе
пропускания
,
допустимое искажение в полосе
пропускания ![]() и
требуемое подавление в полосе
заграждения
и
требуемое подавление в полосе
заграждения ![]() .
.
Первый
шаг: из выражения (1) рассчитываются
параметры ![]() ,
, ![]() ,
и
.
,
и
.
Второй
шаг — расчет требуемого порядка
фильтра ![]() согласно
выражению (4).
согласно
выражению (4).
Третий шаг пересчет параметра согласно следующему выражению:
|
(5) |
Смысл
пересчета параметра
заключается
в том, что при расчете порядка
фильтра
согласно
выражению (4), мы округляем
до
ближайшего целого, в результате мы
меняем параметры эллиптической
дробно-рациональной функции. Так на
рисунках 2-4 показаны АЧХ эллиптического
фильтра при различном
и
фиксированном ![]() .
Из рисунков 2-4 видно, что увеличение
порядка
при
фиксированном
приводит
к изменению уровня боковых лепестков
при аппроксимации АЧХ фильтра. В
результате фильтр рассчитывается с
большим запасом по уровню подавления
сигнала в полосе заграждения.
.
Из рисунков 2-4 видно, что увеличение
порядка
при
фиксированном
приводит
к изменению уровня боковых лепестков
при аппроксимации АЧХ фильтра. В
результате фильтр рассчитывается с
большим запасом по уровню подавления
сигнала в полосе заграждения.
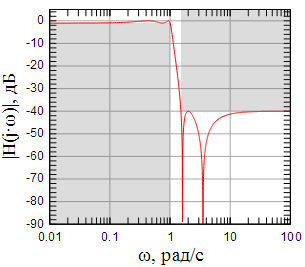
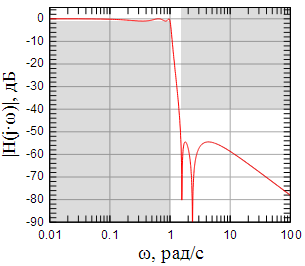
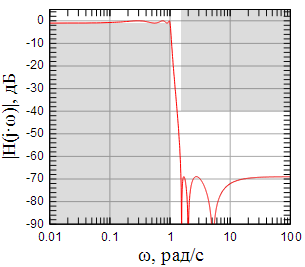
Рисунок
2: АЧХ эллиптического фильтра при
|
Рисунок
3: АЧХ эллиптического фильтра при |
Рисунок
4: АЧХ эллиптического фильтра при |
С другой стороны, эллиптическая дробно-рациональная функция допускает изменение модуля , тем самым появляется возможность оставить уровень подавления в полосе заграждения постоянным (ни у фильтров Чебышева ни у фильтров Баттерворта подобного параметра нет). Для этого и применяют выражение (5). Так на рисунках 5-7 показаны АЧХ эллиптических фильтров различного порядка с пересчитанными согласно (5) модулями .
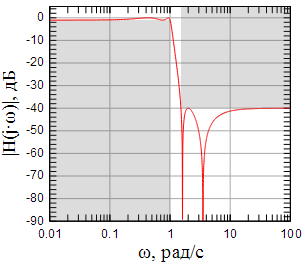
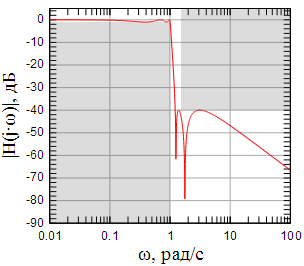
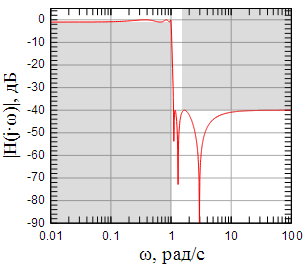
Рисунок 5: АЧХ эллиптического фильтра при |
Рисунок
6: АЧХ эллиптического фильтра при |
Рисунок
7: АЧХ эллиптического фильтра при |
Видно, что все фильтры имеют одинаковый уровень боковых лепестков в полосе заграждения, но при увеличении порядка фильтра сужается переходная полоса фильтра. Таким образом, важно понять, что при округлении порядка фильтра необходимо произвести пересчет модуля для обеспечения заданного уровня боковых лепестков АЧХ фильтра.
Шаг 4. расчет передаточной функции эллиптического фильтра. Здесь как и ранее мы остановимся более подробно.
Нули и полюса эллиптического фильтра
Предварительно очень рекомендую еще раз обратится к рекуррентным соотношениям для расчета эллиптических функций при помощи преобразования Ландена, так как они являются основным вычислительным инструментом при расчете эллиптических фильтров.
Поскольку ![]() ,
то
,
то ![]() и
выражение (2) можно переписать:
и
выражение (2) можно переписать:
|
(6) |
Эллиптическая
дробно-рациональная функция имеет как
нули так и полюса. Тогда согласно
(6) ![]() обращается
в ноль, когда знаменатель выражения (2)
равен бесконечности. Другими словами,
нули эллиптического фильтра совпадают
с полюсами эллиптической дробно-рациональной
функции и находятся из уравнения:
обращается
в ноль, когда знаменатель выражения (2)
равен бесконечности. Другими словами,
нули эллиптического фильтра совпадают
с полюсами эллиптической дробно-рациональной
функции и находятся из уравнения:
|
(7) |
решение которого можно представить:
|
(8) |
С учетом (6), нули эллиптического фильтра можно записать:
|
(9) |
Полюса эллиптического фильтра можно найти решив уравнение
|
(10) |
Мы не будем решать данное уравнение, а приведем выражения для полюсов эллиптического фильтра, расположенных в левой полуплоскости в окончательном виде для четного порядка фильтра:
|
(11) |
Для
нечетного порядка
дополнительно
будет еще один некратный чисто вещественный
полюс ![]() :
:
|
(12) |
Р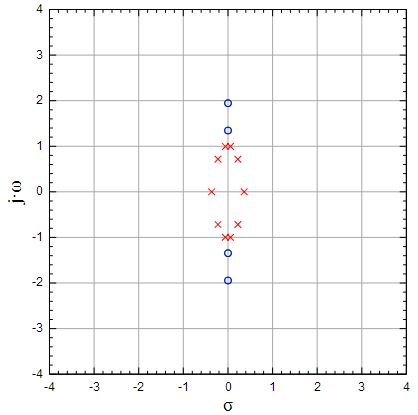
 асположение
нулей и полюсов эллиптического фильтра
на комплексной плоскости для фильтра
четного и нечетного порядков при
подавлении в полосе заграждения равном
45 дБ показано на рисунках 8 и 9.
асположение
нулей и полюсов эллиптического фильтра
на комплексной плоскости для фильтра
четного и нечетного порядков при
подавлении в полосе заграждения равном
45 дБ показано на рисунках 8 и 9.
Рисунок 8: Расположение нулей и полюсов эллиптического фильтра 5-го порядка |
Рисунок 9: Расположение нулей и полюсов эллиптического фильтра 6-го порядка |
Красными крестиками обозначены полюса фильтра, а синими кружочками — нули. Видно, что у фильтра нечетного порядка имеются чисто вещественные полюса. Обратите внимание, что нули и полюса отображены в одинаковом масштабе. Все полюса фильтра расположены на эллипсе, как и у фильтра Чебышева первого рода, но в отличии от фильтра Чебышева первого рода, эллиптический фильтр имеет нули, как и инверсный фильтр Чебышева. Это позволяет регулировать как неравномерность АЧХ в полосе пропускания, так и уровень подавления в полосе заграждения.
Передаточная характеристика эллиптического фильтра
Зная нули и полюса эллиптического фильтра, выразив из них только полюса, лежащие в левой полуплоскости можно получить передаточную характеристику фильтра в виде:
|
(13) |
Для
представления передаточной характеристики
эллиптического фильтра при помощи
биквадратной формы заметим, что в случае
нечетного порядка ![]() имеется
не кратный вещественный полюс. При
остальных
полюса
будут комплексно-сопряженные. Тогда
для любого
,
где
имеется
не кратный вещественный полюс. При
остальных
полюса
будут комплексно-сопряженные. Тогда
для любого
,
где ![]() может
принимать значения 0 или 1, передаточную
функцию эллиптического фильтра можно
записать через биквадратную форму:
может
принимать значения 0 или 1, передаточную
функцию эллиптического фильтра можно
записать через биквадратную форму:
|
(14) |
где ![]() и
и ![]() -
реальная и мнимая части соответственно.
-
реальная и мнимая части соответственно.
Тогда,
коэффициент передачи на нулевой частоте
фильтра при ![]() равен:
равен:
|
(15) |
Также
необходимо учесть, что как и в случае с
фильтром Чебышева первого рода,
эллиптический фильтр на нулевой частоте
имеет коэффициент передачи равный ![]() .
Тогда окончательно можно передаточную
характеристику эллиптического фильтра
для порядка
представить
в виде:
.
Тогда окончательно можно передаточную
характеристику эллиптического фильтра
для порядка
представить
в виде:
|
(16) |
Пример расчета эллиптического фильтра
Рассчитаем нормированный эллиптический ФНЧ исходя из следующего коридора АЧХ:
|
(17) |
Шаг 1. Из выражения (1) рассчитаем параметры коридора:
|
(18) |
Шаг 2. Рассчитаем порядок фильтра удовлетворяющий заданному коридору согласно выражению (4). Для этого предварительно при помощи преобразования Ландена рассчитаем полные и комплиментарные эллиптические интегралы:
|
(19) |
Тогда порядок фильтра равен:
|
(20) |
Округляем
в большую сторону, таким образом порядок
фильтра ![]() .
.
Шаг
3. Пересчет эллиптического модуля
согласно выражению (5). Предварительно
представим ![]() ,
откуда
,
откуда![]() ,
, ![]() .
Тогда
.
Тогда
|
(21) |
Пересчитываем модуль :
|
(22) |
Вычисление
эллиптических функций ![]() производилось
также при помощи преобразования Ландена.
производилось
также при помощи преобразования Ландена.
Шаг 4. Расчет нулей и полюсов фильтра.
Нули фильтра рассчитываются согласно (16):
|
(23) |
Рассчитаем полюса фильтра. Для этого предварительно рассчитаем:
|
(24) |
Тогда полюса согласно выражению (16):
|
(25) |
Поскольку , то рассчитываем некратный полюс :
|
(26) |
Шаг 5. Рассчитываем передаточную характеристику на основе биквадратной формы согласно выражению (16). Для этого произведем предварительно расчет коэффициента передачи на нулевой частоте для нормировки фильтра.
|
(27) |
Поскольку фильтр нечетного порядка, то учитывать не требуется.
Передаточная характеристика фильтра равна:
|
(28) |
На этом расчет эллиптического фильтра можно считать оконченным.
Подставив
в выражение для передаточной
характеристики
получим
комплексный коэффициент передачи![]() из
которого можно рассчитать АЧХ, ФЧХ и
групповую задержку фильтра. На рисунках
10 - 12 показаны графики АЧХ, ФЧХ и групповой
задержки рассчитанного фильтра
из
которого можно рассчитать АЧХ, ФЧХ и
групповую задержку фильтра. На рисунках
10 - 12 показаны графики АЧХ, ФЧХ и групповой
задержки рассчитанного фильтра
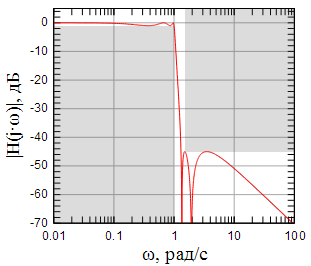
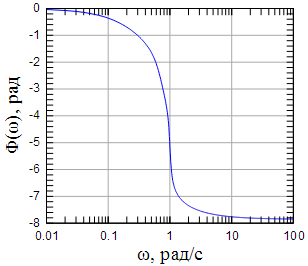
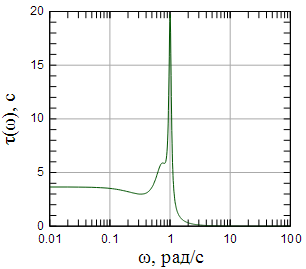
Рисунок 10: АЧХ рассчитанного фильтра |
Рисунок 11: ФЧХ рассчитанного фильтра |
Рисунок 12: Групповая задержка рассчитанного фильтра |
На графике АЧХ серым цветом отмечен заданный коридор в который помещается АЧХ рассчитанного фильтра. Как видно из рисунка фильтр полностью укладывается в заданный коридор АЧХ.
Выводы
В данной статье мы рассмотрели расчет аналогового нормированного ФНЧ Кауэра (эллиптический фильтр). Были получены выражения для нулей и полюсов эллиптического фильтра , показано геометрическое расположение нулей и полюсов на комплексной плоскости. Приведено выражение для передаточной характеристики фильтра на основе биквадратной формы для четного и нечетного порядков фильтра. Показан вид АЧХ эллиптического фильтра и рассмотрен пример расчета фильтра по заданному коридору АЧХ.
Аппроксимация передаточной характеристики аналогового фильтра нижних частот по Чебышеву.
Расчет аналогового нормированного ФНЧ Чебышева первого рода
Содержание
Введение. Исходные данные и основные соотношения при аппроксимации АЧХ фильтра
Порядок расчета фильтра Чебышева первого рода
Нули и полюса фильтра Чебышева первого рода
Передаточная характеристика фильтра Чебышева первого рода
Пример расчета фильтра Чебышева первого рода
Выводы
Введение. Исходные данные и основные соотношения при аппроксимации АЧХ фильтра
В предыдущей статье мы рассмотрели основные свойства полиномов комплексной переменной и передаточной функции аналогового фильтра . Также была рассмотрена постановка задачи расчета фильтра, и проанализированы основные виды аппроксимирующих полиномов АЧХ.
В данной статье мы рассмотрим расчет фильтра Чебышева первого рода по заданному коридору АЧХ, показанному на рисунке 1.
 Рисунок
1: Идеальная и реальная АЧХ ФНЧ
Рисунок
1: Идеальная и реальная АЧХ ФНЧ
Приведем основные соотношения связывающие параметры аппроксимации АЧХ (данные соотношения были подробно рассмотрены здесь):
|
(1) |
Аппроксимация АЧХ ФНЧ Чебышева первого рода представляется в виде:
|
(2) |
где - многочлен Чебышева.
Порядок фильтра Чебышева первого рода рассчитывается из уравнения:
|
(3) |
Решение которого имеет вид:
|
(4) |
где - арккосинус гиперболический.
Все вышеприведенные соотношения уже были рассмотрены ранее. Мы привели их еще раз без пояснений, и они нам будут необходимы при рассечет фильтра Чебышева первого рода.
Порядок расчета фильтра Чебышева первого рода
Итак приступим. Исходными данными для расчета фильтра Чебышева первого рода служат: частота среза , переходная полоса, задаваемая , допустимое искажение в полосе пропускания и требуемое подавление в полосе заграждения .
Первый шаг: из выражения (1) рассчитываются параметры , , и .
Второй шаг: расчет требуемого порядка фильтра согласно выражению (4).
Третий шаг, на котором мы остановимся более подробно: расчет передаточной функции фильтра Чебышева.
Нули и полюса фильтра Чебышева первого рода
Предварительно
мы вспомним некоторые свойства
тригонометрических функций комплексного
переменного. Во первых, рассмотрим
косинус комплексной переменной ![]() .
Представим как косинус суммы и получим:
.
Представим как косинус суммы и получим:
|
(5) |
Учтем, что тригонометрические функции связаны с гиперболическими следующими соотношениями:
|
(6) |
Тогда
окончательно можно представить выражение
(5), с учетом выражения (6) ![]() и:
и:
|
(7) |
Соотношение (7) мы будем широко использовать в дальнейшем. Также вспомним следующее соотношение справедливое для произведения комплексно-споряженных чисел:
|
(8) |
Данное соотношение нам также очень пригодится.
Итак приступим к расчету передаточной функции фильтра Чебышева первого рода. Как и в случае с фильтром Баттерворта, для фильтра Чебышева мы рассчитаем нули и полюса квадрата модуля переаточной характеристики, выберем из них только те, что лежат в левой полуплоскости (с отрицательной реальной частью) для обеспечения физической реализуемости и устойчивости фильтра, и после представим передаточную функцию фильтра на основе биквадратной формы.
Как
и в случае фильтра Баттерворта, фильтр
Чебышева не имеет нулей, так как ни при
каких комплексных значениях ![]() квадрат
модуля передаточной функции фильтра
Чебышева (2) не обращается в ноль. Для
расчета полюсов фильтра Чебышева
приравняем знаменатель (2) к нулю:
квадрат
модуля передаточной функции фильтра
Чебышева (2) не обращается в ноль. Для
расчета полюсов фильтра Чебышева
приравняем знаменатель (2) к нулю:
|
(9) |
Учтем
что ![]() ,
тогда уравнение (9) перепишется к виду:
,
тогда уравнение (9) перепишется к виду:
|
(10) |
Учтем (8), тогда выражение (10) можно представить в виде произведения комплексно-сопряженных выражений:
|
(11) |
Уравнение (11) можно переписать:
|
(12) |
Теперь нам надо решить уравнение (12) относительно . Для этого введем обозначение
|
(13) |
тогда
|
(14) |
Или с учетом соотношения (7) можно записать:
|
(15) |
Приравняем реальные и мнимые слагаемые в левой и правой частях уравнения и получим систему:
|
(16) |
Рассмотрим
систему подробнее. Гиперболический
косинус ![]() никогда
не обращается в ноль. Поэтому первое
уравнение (16) можно записать:
никогда
не обращается в ноль. Поэтому первое
уравнение (16) можно записать:
|
(17) |
Из
второго уравнения, с учетом (17) можно
заметить, что ![]() и
тогда
и
тогда
|
(18) |
Таким
образом, мы рассчитали значения ![]() и
и ![]() в
выражении (13). Теперь необходимо решить
уравнение (13) относительно
.
в
выражении (13). Теперь необходимо решить
уравнение (13) относительно
.
|
(19) |
Откуда с учетом выражения (7) можно записать:
|
(20) |
Тогда окончательно полюса квадрата модуля АЧХ фильтра Чебышева первого рода можно записать с учетом (17) и (18):
|
(21) |
Для анализа расположения полюсов фильтра Чебышева рассмотрим соотношение:
|
(22) |
Тогда вспомнив каноническое уравнение эллипса :
|
(23) |
можно сделать вывод о том, что полюса фильтра Чебышева первого рода расположены на эллипсе с осями:
|
(24) |
Графически это показано на рисунке 2 для и на рисунке 3 для .
Рисунок 2: Расположение полюсов квадрата модуля АЧХ фильтра Чебышева первого рода при |
Рисунок 3: Расположение полюсов квадрата модуля АЧХ фильтра Чебышева первого рода при |
Красными
крестиками показаны полюса фильтра
Чебышева. Зеленым показана окружность
радиуса ![]() и
полюса фильтра
Баттерворта при
и
при
неравномерности фильтра Баттерворта
равной
и
полюса фильтра
Баттерворта при
и
при
неравномерности фильтра Баттерворта
равной ![]() .
Аналогично синим показана окружность
радиуса
.
Аналогично синим показана окружность
радиуса ![]() и
полюса фильтра Баттерворта при
и
и
при неравномерности фильтра Баттерворта
равной
и
полюса фильтра Баттерворта при
и
и
при неравномерности фильтра Баттерворта
равной ![]() .
Синими и зелеными линиями показано
геометрическое расположение полюсов
фильтра Чебышева первого рода, относительно
полюсов « большого » и « малого » фильтров
Баттерворта. Важно отметить, что если
малую ось эллипса приближать к большой
оси, то фильтр Чебышева будет приближаться
к фильтру Баттерворта. Если эллипс на
котором расположены полюса фильтра
Чебышева превратить в окружность, то
фильтр Чебышева автоматически переходит
в фильтр Баттерворта. Другими словами
если
.
Синими и зелеными линиями показано
геометрическое расположение полюсов
фильтра Чебышева первого рода, относительно
полюсов « большого » и « малого » фильтров
Баттерворта. Важно отметить, что если
малую ось эллипса приближать к большой
оси, то фильтр Чебышева будет приближаться
к фильтру Баттерворта. Если эллипс на
котором расположены полюса фильтра
Чебышева превратить в окружность, то
фильтр Чебышева автоматически переходит
в фильтр Баттерворта. Другими словами
если ![]() ,
то согласно (24) необходимо чтобы
,
то согласно (24) необходимо чтобы
|
(25) |
Таким образом при уменьшении неравномерности в полосе пропускания фильтра Чебышева первого рода, его характеристика приближается к характеристики фильтра Баттерворта.
Передаточная характеристика фильтра Чебышева первого рода
Для
получения передаточной характеристики
физически реализуемого фильтра
необходимо, чтобы все его нули и полюса
располагались в левой полуплоскости.
Тогда из всех полюсов фильтра Чебышева
(21) необходимо выбрать только те, у
которых![]() ,
тогда все полюса фильтра Чебышева можно
представить в виде:
,
тогда все полюса фильтра Чебышева можно
представить в виде:
|
(26) |
Передаточная характеристика фильтра Чебышева первого рода будет иметь вид:
|
(27) |
Для
представления передаточной характеристики
фильтра Чебышева первого рода при помощи
биквадратной формы заметим, что в случае
нечетного порядка ![]() при
при ![]() получим
получим ![]() некратный
вещественный полюс (смотри рисунок 2).
При остальных
полюса
будут комплексно-сопряженные. Тогда
для любого
,
где
может
принимать значения 0 или 1 передаточную
функцию фильтра Чебышева первого рода
можно записать через биквадратную
форму:
некратный
вещественный полюс (смотри рисунок 2).
При остальных
полюса
будут комплексно-сопряженные. Тогда
для любого
,
где
может
принимать значения 0 или 1 передаточную
функцию фильтра Чебышева первого рода
можно записать через биквадратную
форму:
|
(28) |
Тогда,
коэффициент передачи на нулевой частоте
фильтра при ![]() равен:
равен:
|
(29) |
Кроме
того при нормировке необходимо учесть,
что при нечетных порядках фильтра,
многочлен Чебышева ![]() и
соответственно
и
соответственно ![]() согласно
выражению (2), а при четных порядках
фильтра, многочлен Чебышева
согласно
выражению (2), а при четных порядках
фильтра, многочлен Чебышева ![]() и
соответственно
и
соответственно ![]() ,
таким образом, при четном порядке
фильтра, его коэффициент передачи на
нулевой частоте должен быть меньше
единицы и равен
,
таким образом, при четном порядке
фильтра, его коэффициент передачи на
нулевой частоте должен быть меньше
единицы и равен ![]() .
С учетом этого передаточная функция
нормированного фильтра Чебышева 1 рода
для любого
имеет
вид:
.
С учетом этого передаточная функция
нормированного фильтра Чебышева 1 рода
для любого
имеет
вид:
|
(30) |
На рисунках 4 - 9 показаны АЧХ , ФЧХ и групповая задержка фильтров Чебышева первого рода 4-го и 5-го порядков с неравномерностью АЧХ в полосе пропускания 2 дБ.
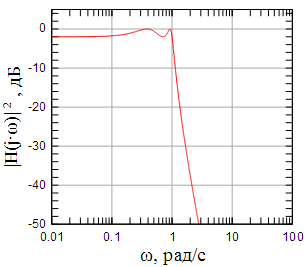
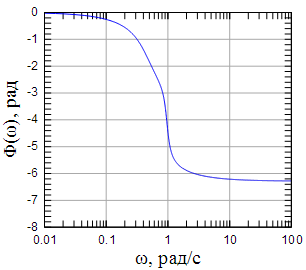
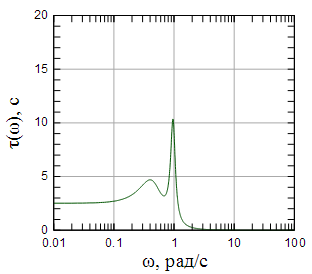
Рисунок 4: АЧХ фильтра Чебышева первого рода 4-го порядка |
Рисунок 5: ФЧХ фильтра Чебышева первого рода 4-го порядка |
Рисунок 6: Групповая задержка фильтра Чебышева первого рода 4-го порядка |
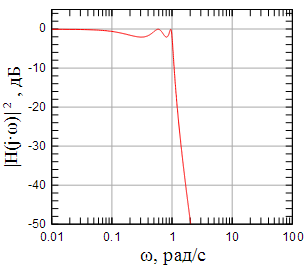
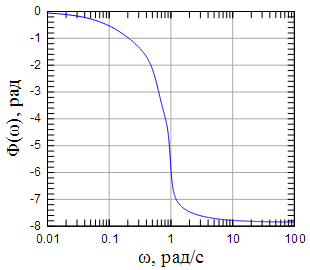
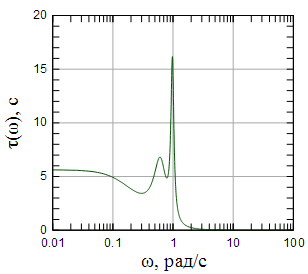
Рисунок 7: АЧХ фильтра Чебышева первого рода 5-го порядка |
Рисунок 8: ФЧХ фильтра Чебышева первого рода 5-го порядка |
Рисунок 9: Групповая задержка фильтра Чебышева первого рода 5-го порядка |
Из графиков хорошо видно, что АЧХ фильтра Чебышева имеет равноволновые колебания в полосе пропускания и монотонно убывает в полосе заграждения.
Пример расчета фильтра Чебышева первого рода
Рассчитаем нормированный ФНЧ Чебышева первого рода исходя из следующего коридора АЧХ:
|
(31) |
Шаг 1. Из выражения (1) рассчитаем параметры коридора:
|
(32) |
Шаг 2. Рассчитаем порядок фильтра удовлетворяющий заданному коридору согласно выражению (4):
|
(33) |
Округляем в большую сторону, таким образом порядок фильтра .
Шаг 3. Рассчитываем передаточную характеристику на основе биквадратной формы согласно выражению (30). Для этого произведем предварительные расчеты.
Порядок
фильтр ![]() ,
откуда
,
откуда ![]() .
Параметр
равен:
.
Параметр
равен:
|
(34) |
Параметры ![]() где
принимает
значения 1 или 2 равны:
где
принимает
значения 1 или 2 равны:
|
(35) |
Рассчитаем
параметры ![]() и
и ![]() ,
а также рассчитаем
,
а также рассчитаем ![]() :
:
|
(36) |
Обратим
внимание, что ![]() и
рассчитывать параметр
и
рассчитывать параметр ![]() не
требуется. Теперь можно рассчитать
передаточную характеристику фильтра:
не
требуется. Теперь можно рассчитать
передаточную характеристику фильтра:
|
(37) |
После раскрытия скобок и приведения подобных слагаемых получим передаточную характеристику в окончательном виде:
|
(38) |
На этом расчет фильтра Чебышева первого рода можно считать оконченным.
Подставив
в выражение для передаточной
характеристики
получим
комплексный коэффициент передачи![]() из
которого можно рассчитать АЧХ, ФЧХ и
групповую задержку фильтра. На рисунках
10 - 12 показаны графики АЧХ, ФЧХ и групповой
задержки рассчитанного фильтра.
из
которого можно рассчитать АЧХ, ФЧХ и
групповую задержку фильтра. На рисунках
10 - 12 показаны графики АЧХ, ФЧХ и групповой
задержки рассчитанного фильтра.
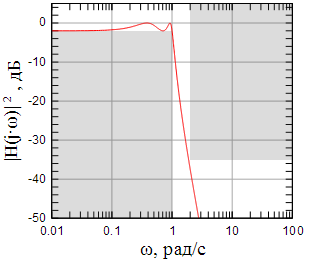
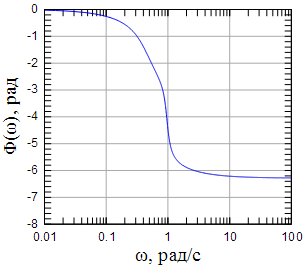
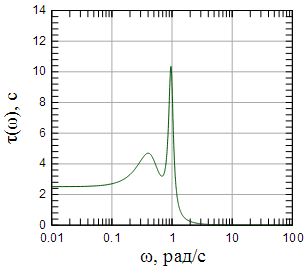
Рисунок 10: АЧХ рассчитанного фильтра |
Рисунок 11: ФЧХ рассчитанного фильтра |
Рисунок 12: Групповая задержка рассчитанного фильтра |
На графике АЧХ серым цветом отмечен заданный коридор в который помещается АЧХ рассчитанного фильтра. Как видно из рисунка 10, АЧХ полностью укладывается в заданный коридор АЧХ.
Выводы
В данной статье мы рассмотрели расчет аналогового нормированного ФНЧ Чебышева первого рода. Были получены выражения для нулей и полюсов фильтра Чебышева первого рода, показано геометрическое расположение нулей и полюсов на комплексной плоскости. Приведено выражение для передаточной характеристики фильтра Чебышева первого рода на основе биквадратной формы для четного и нечетного порядков фильтра. Показан вид АЧХ фильтра Чебышева первого рода и рассмотрен пример расчета фильтра по заданному коридору АЧХ.
Расчет аналогового нормированного ФНЧ Чебышева второго рода
Содержание
Введение. Исходные данные и основные соотношения при аппроксимации АЧХ фильтра
Порядок расчета фильтра Чебышева второго рода
Нули и полюса фильтра Чебышева второго рода
Передаточная характеристика фильтра Чебышева второго рода
Пример расчета фильтра Чебышева второго рода
Выводы
Введение. Исходные данные и основные соотношения при аппроксимации АЧХ фильтра
В
предыдущей статье мы рассмотрели
основные свойства полиномов комплексной
переменной и передаточной функции
аналогового фильтра ![]() .
Также была рассмотрена постановка
задачи расчета фильтра, и проанализированы
основные виды аппроксимирующих полиномов
АЧХ фильтра.
.
Также была рассмотрена постановка
задачи расчета фильтра, и проанализированы
основные виды аппроксимирующих полиномов
АЧХ фильтра.
В данной статье мы рассмотрим расчет фильтра Чебышева второго рода (инверсный фильтр Чебышева) по заданному коридору АЧХ, показанному на рисунке 1.
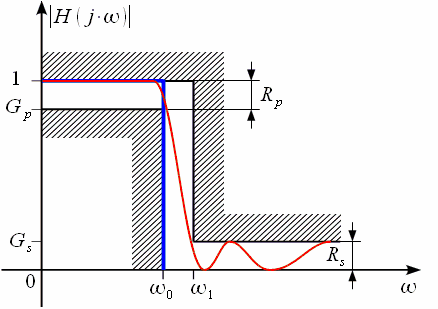 Рисунок
1: Идеальная и реальная АЧХ ФНЧ
Рисунок
1: Идеальная и реальная АЧХ ФНЧ
В отличие от фильтров Чебышева первого рода, инверсные фильтры Чебышева обладают гладкой АЧХ в полосе пропускания и обеспечивают заданный уровень подавления в полосе заграждения.
Приведем основные соотношения связывающие параметры аппроксимации АЧХ (данные соотношения были подробно рассмотрены здесь):
|
(1) |
Аппроксимация АЧХ ФНЧ Чебышева второго рода представляется в виде:
|
(2) |
где ![]() -
многочлен Чебышева.
-
многочлен Чебышева.
Порядок фильтра Чебышева второго рода рассчитывается из уравнения:
|
(3) |
Решение которого имеет вид:
|
(4) |
где ![]() -
арккосинус гиперболический.
-
арккосинус гиперболический.
Все вышеприведенные соотношения уже были рассмотрены ранее. Мы привели их еще раз без пояснений, и они нам будут необходимы при рассечет фильтра Чебышева второго рода.
Порядок расчета фильтра Чебышева второго рода
Итак
приступим. Исходными данными для расчета
фильтра Чебышева второго рода служат:
частота среза ![]() ,
переходная полоса, задаваемая
,
переходная полоса, задаваемая ![]() ,
допустимое искажение в полосе
пропускания
,
допустимое искажение в полосе
пропускания ![]() и
требуемое подавление в полосе заграждения
и
требуемое подавление в полосе заграждения![]() .
.
Первый
шаг: из выражения (1) рассчитываются
параметры ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
Второй
шаг расчет требуемого порядка
фильтра ![]() согласно
выражению (4).
согласно
выражению (4).
Далее необходимо произвести расчет передаточной функции фильтра Чебышева второго рода. И здесь мы остановимся подробнее
Нули и полюса фильтра Чебышева второго рода
Предварительно
мы вспомним некоторые свойства
тригонометрических функций комплексного
переменного. Во первых рассмотрим
косинус комплексной переменной ![]() .
Представим как косинус суммы и получим:
.
Представим как косинус суммы и получим:
|
(5) |
Учтем, что тригонометрические функции связаны с гиперболическими следующими соотношениями:
|
(6) |
Тогда
окончательно можно представить выражение
(5), с учетом выражения (6) ![]() и:
и:
|
(7) |
Соотношение (7) мы будем широко использовать в дальнейшем. Также вспомним следующее соотношение справедливое для произведения комплексно-споряженных чисел:
|
(8) |
Данное соотношение нам также очень пригодится.
Итак приступим к расчету передаточной функции фильтра Чебышева второго рода. Порядок расчета очень похож на тот, что мы использовали при расчете фильтра Чебышева первого рода. Для фильтра Чебышева второго рода мы рассчитаем нули и полюса квадрата модуля передаточной характеристики, выберем из них только те, что лежат в левой полуплоскости (с отрицательной реальной частью) для обеспечения физической реализуемости и устойчивости фильтра, и после представим передаточную функцию фильтра на основе биквадратной формы.
В отличие от фильтра Чебышева первого рода, инверсный фильтр Чебышева имеет нули, которые находятся из уравнения:
|
(9) |
Учтем
что ![]() ,
тогда уравнение (9) примит вид:
,
тогда уравнение (9) примит вид:
|
(10) |
Откуда
можно получить выражение для нулей
фильтра Чебышева второго рода ![]() :
:
|
(11) |
Нули фильтра Чебышева второго рода всегда чисто мнимые и по модулю больше нуля. Расположение нулей на комплексной плоскости будет показано ниже. Пока же мы получим выражение для полюсов фильтра Чебышева второго рода. Порядок расчета полюсов фильтра Чебышева второго рода тот же, что и порядок расчета полюсов фильтра Чебышева первого рода.
Для расчета полюсов фильтра Чебышева приравняем знаменатель (2) к нулю:
|
(12) |
Учтем (8), тогда выражение (12) можно представить в виде произведения комплексно-сопряженных выражений:
|
(13) |
Уравнение (13) можно переписать:
|
(14) |
Теперь
нам надо решить уравнение (14) относительно ![]() .
Для этого введем обозначение
.
Для этого введем обозначение
|
(15) |
Тогда
|
(16) |
Или с учетом соотношения (7) можно записать:
|
(17) |
Приравняем реальные и мнимые части в левой и правой частях уравнения и получим систему:
|
(18) |
Рассмотрим
систему подробнее. Гиперболический
косинус ![]() никогда
не обращается в ноль. Поэтому первое
уравнение (18) можно записать:
никогда
не обращается в ноль. Поэтому первое
уравнение (18) можно записать:
|
(19) |
Из
второго уравнения, с учетом (19) можно
заметить, что ![]() и
тогда
и
тогда
|
(20) |
Таким
образом, мы рассчитали значения ![]() и
и ![]() в
выражении (15). Теперь необходимо решить
уравнение (15) относительно
:
в
выражении (15). Теперь необходимо решить
уравнение (15) относительно
:
|
(21) |
Откуда с учетом выражения (7) можно записать:
|
(22) |
Тогда окончательно полюса квадрата модуля АЧХ фильтра Чебышева второго рода можно записать с учетом (19) и (20):
|
(23) |
Для
получения передаточной характеристики
физически реализуемого фильтра необходимо
чтобы все его нули и полюса располагались
в левой полуплоскости. Тогда из всех
полюсов фильтра Чебышева (23) необходимо
выбрать только те, у которых![]() ,
тогда все полюса фильтра Чебышева можно
представить в виде:
,
тогда все полюса фильтра Чебышева можно
представить в виде:
|
(24) |
Р
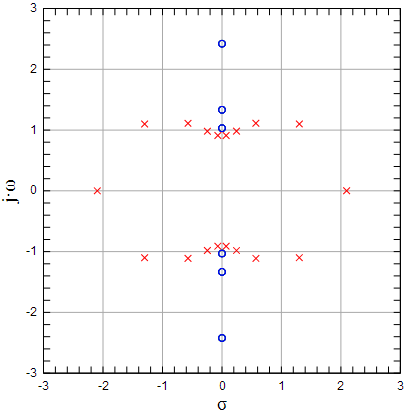 асположение
нулей и полюсов фильтра Чебышева второго
рода на комплексной плоскости представлено
для фильтра четного и нечетного порядков
при подавлении в полосе заграждения
равном 30 дБ показано на рисунках 2 и 3.
асположение
нулей и полюсов фильтра Чебышева второго
рода на комплексной плоскости представлено
для фильтра четного и нечетного порядков
при подавлении в полосе заграждения
равном 30 дБ показано на рисунках 2 и 3.
Рисунок 2: Расположение нулей и полюсов фильтра Чебышева второго рода 8-го порядка |
Рисунок 3: Расположение нулей и полюсов фильтра Чебышева второго рода 9-го порядка |
Красными крестиками обозначены полюса фильтра, а синими кружочками — нули. Видно, что у фильтра нечетного порядка имеется чисто вещественные полюса. Обратите внимание, что нули и полюса отображены в одинаковом масштабе, что привело к тому, что не все нули фильтра нашли отражение на рисунках 2 и 3.
Передаточная характеристика фильтра Чебышева второго рода
Зная нули и полюса фильтра Чебышева второго рода, передаточная характеристика будет иметь вид:
|
(25) |
Для
представления передаточной характеристики
фильтра Чебышева второго рода при помощи
биквадратной формы заметим, что в случае
нечетного порядка ![]() при
при ![]() получим
получим ![]() не
кратный вещественный полюс. При
остальных
полюса
будут комплексно-сопряженные. Тогда
для любого
не
кратный вещественный полюс. При
остальных
полюса
будут комплексно-сопряженные. Тогда
для любого ![]() ,
где
,
где ![]() может
принимать значения 0 или 1 передаточную
функцию фильтра Чебышева второго рода
можно записать через биквадратную
форму:
может
принимать значения 0 или 1 передаточную
функцию фильтра Чебышева второго рода
можно записать через биквадратную
форму:
|
(26) |
Тогда,
коэффициент передачи на нулевой частоте
фильтра при ![]() равен:
равен:
|
(27) |
На
рисунках 4 - 9 показаны АЧХ ![]() ,
ФЧХ
,
ФЧХ ![]() и
групповая задержка
и
групповая задержка ![]() фильтров
Чебышева второго рода 8-го и 9-го порядков
с подавлением в полосе заграждения
равным 30 дБ (нули и полюса данных фильтров
показаны на рисунках 2 и 3).
фильтров
Чебышева второго рода 8-го и 9-го порядков
с подавлением в полосе заграждения
равным 30 дБ (нули и полюса данных фильтров
показаны на рисунках 2 и 3).
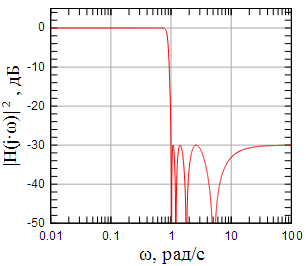
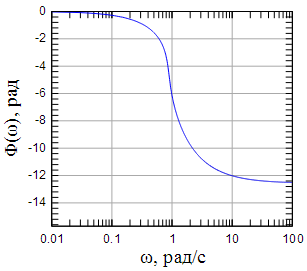
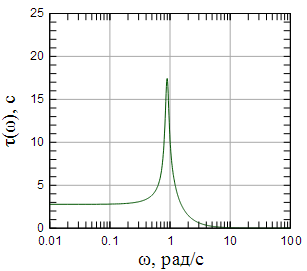
Рисунок 4: АЧХ фильтра Чебышева второго рода 8-го порядка |
Рисунок 5: ФЧХ фильтра Чебышева второго рода 8-го порядка |
Рисунок 6: Групповая задержка фильтра Чебышева второго рода 8-го порядка |
|
|
|
Рисунок 7: АЧХ фильтра Чебышева второго рода 9-го порядка |
Рисунок 8: ФЧХ фильтра Чебышева второго рода 9-го порядка |
Рисунок 9 : Групповая задержка фильтра Чебышева второго рода 9-го порядка |
Из
графиков хорошо видно, что АЧХ фильтра
Чебышева второго рода имеет гладкую
АЧХ в полосе пропускания и равноволновые
колебания в полосе заграждения,
обеспечивая тем самым заданный уровень
подавления . При этом можно заметить,
что АЧХ при четном порядке фильтра при
увеличении частоты стремится к значению ![]() ,
а при нечетном порядке фильтра к нулю.
,
а при нечетном порядке фильтра к нулю.
Пример расчета фильтра Чебышева второго рода
Рассчитаем нормированный ФНЧ Чебышева второго рода исходя из следующего коридора АЧХ:
|
(28) |
Шаг 1. Из выражения (1) рассчитаем параметры коридора:
|
(29) |
Шаг 2. Рассчитаем порядок фильтра удовлетворяющий заданному коридору согласно выражению (4):
|
(30) |
Округляем
в большую сторону, таким образом порядок
фильтра ![]() .
.
Шаг 3. Рассчитываем передаточную характеристику на основе биквадратной формы согласно выражению (26). Для этого произведем предварительные расчеты.
Порядок
фильтр ![]() ,
откуда
,
откуда ![]() .
Параметр
равен:
.
Параметр
равен:
|
(31) |
Параметры ![]() где
принимает
значения 1 или 2 равны:
где
принимает
значения 1 или 2 равны:
|
(32) |
Тогда нули передаточной функции равны:
|
(33) |
Рассчитаем
параметры ![]() и
и ![]() ,
а также рассчитаем
,
а также рассчитаем ![]() :
:
|
(34) |
Обратим
внимание, что ![]() и
требуется также рассчитать параметр
и
требуется также рассчитать параметр ![]() :
:
|
(35) |
Рассчитаем
нормировочный коэффициент ![]() согласно
выражению (27):
согласно
выражению (27):
|
(36) |
Теперь можно рассчитать передаточную характеристику фильтра:
|
(37) |
На этом расчет фильтра Чебышева второго рода можно считать оконченным.
Подставив
в выражение для передаточной
характеристики
получим
комплексный коэффициент передачи![]() из
которого можно рассчитать АЧХ, ФЧХ и
групповую задержку фильтра. На рисунках
10 - 12 показаны графики АЧХ, ФЧХ и групповой
задержки рассчитанного фильтра
из
которого можно рассчитать АЧХ, ФЧХ и
групповую задержку фильтра. На рисунках
10 - 12 показаны графики АЧХ, ФЧХ и групповой
задержки рассчитанного фильтра
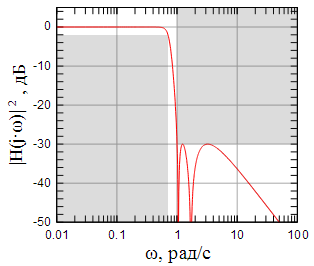
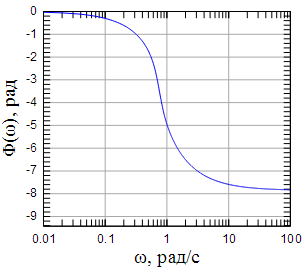
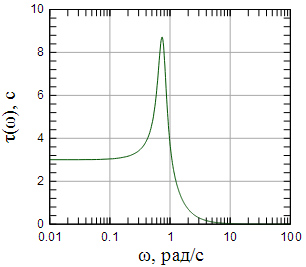
Рисунок 10: АЧХ рассчитанного фильтра |
Рисунок 11: ФЧХ рассчитанного фильтра |
Рисунок 12: Групповая задержка рассчитанного фильтра |
На графике АЧХ серым цветом отмечен заданный коридор в который помещается АЧХ рассчитанного фильтра.
Как видно из рисунка фильтр полностью укладывается в заданный коридор АЧХ.
Выводы
В данной статье мы рассмотрели расчет аналогового нормированного ФНЧ Чебышева второго рода. Были получены выражения для нулей и полюсов фильтра Чебышева второго рода, показано геометрическое расположение нулей и полюсов на комплексной плоскости. Приведено выражение для передаточной характеристики фильтра Чебышева второго рода на основе биквадратной формы для четного и нечетного порядков фильтра. Показан вид АЧХ фильтра Чебышева второго рода и рассмотрен пример расчета фильтра по заданному коридору АЧХ.
Построение аналоговых фильтров нижних частот с произвольной частотой среза, верхних частот, полосового, режекторного.
Частотные преобразования фильтров. Преобразование ФНЧ-ФНЧ и ФНЧ-ФВЧ
Содержание
Введение. Постановка задачи
Преобразование ФНЧ-ФНЧ
Расчет ФНЧ с заданной частотой среза на основе коридора АЧХ
Преобразование ФНЧ-ФВЧ
Расчет ФВЧ с заданной частотой среза по заданному коридору АЧХ
Введение. Постановка задачи
В предыдущих статьях мы рассмотрели вопросы расчета аналоговых нормированных фильтров нижних частот. Был рассмотрен расчет фильтров Баттерворта, Чебышева и Кауэра (эллиптических фильтров). Однако это были лишь ФНЧ с частотой среза равной 1 рад/с. На практике требуется рассчитать различные типы фильтров: фильтры верхних частот (ФВЧ), полосовые фильтры (ПФ) и режекторные фильтры (РФ), да и ФНЧ тоже может потребоваться с различной частотой среза. В данной статье мы рассмотрим как нормированный ФНЧ можно пересчитать в любой тип фильтра с заданными характеристиками. Такой пересчет называется частотное преобразование фильтра и строится на дробно-рациональной подстановке, численный расчет которой был представлен здесь.
Пусть
мы рассчитали передаточную характеристику
нормированного ФНЧ ![]() при
использовании выбранной аппроксимации
АЧХ фильтра (Баттерворта, Чебышева или
Кауэра):
при
использовании выбранной аппроксимации
АЧХ фильтра (Баттерворта, Чебышева или
Кауэра):
|
(1) |
Частота
среза нормированного ФНЧ равна ![]() .
Рассмотрим различные частотные
преобразования передаточной
характеристики
.
.
Рассмотрим различные частотные
преобразования передаточной
характеристики
.
Преобразование ФНЧ-ФНЧ
Первое
что мы рассмотрим, это преобразование
нормированного ФНЧ с передаточной
характеристикой
в
ФНЧ, с передаточной характеристикой ![]() ,
но с другой частотой среза
,
но с другой частотой среза ![]() .
При этом очень важно, чтобы неравномерность
в полосе пропускания фильтра и уровень
подавления в полосе заграждения не
изменились. Для этого используют
дробно-рациональную подстановку вида:
.
При этом очень важно, чтобы неравномерность
в полосе пропускания фильтра и уровень
подавления в полосе заграждения не
изменились. Для этого используют
дробно-рациональную подстановку вида:
|
(2) |
Такая подстановка эквивалентна подстановке частоты в выражения для комплексного коэффициента передачи:
|
(3) |
где ![]() -
циклическая частота нормированного
ФНЧ с АЧХ
-
циклическая частота нормированного
ФНЧ с АЧХ ![]() .
Графическое представление частотного
преобразования ФНЧ-ФНЧ показано на
рисунке 1.
.
Графическое представление частотного
преобразования ФНЧ-ФНЧ показано на
рисунке 1.
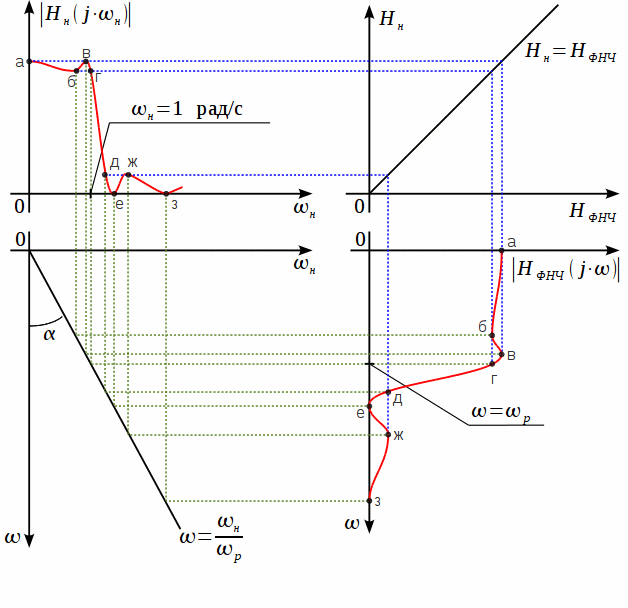 Рисунок
1: Графическое представление частотного
преобразования ФНЧ->ФНЧ
Рисунок
1: Графическое представление частотного
преобразования ФНЧ->ФНЧ
На
верхнем левом графике показана АЧХ
исходного нормированного ФНЧ
,
а на нижнем правом — АЧХ после частотного
преобразования ![]() (повернутая
на 90 градусов). Для того, чтобы
неравномерность в полосе пропускания
и уровень подавления в полосе заграждения
пересчитанного фильтра были такими же,
что и у исходного нормированного ФНЧ,
используют проекцию
(повернутая
на 90 градусов). Для того, чтобы
неравномерность в полосе пропускания
и уровень подавления в полосе заграждения
пересчитанного фильтра были такими же,
что и у исходного нормированного ФНЧ,
используют проекцию ![]() (верхний
правый график), а для преобразования
оси частот используют проекцию (3), как
это показано на нижнем левом графике.
Сами проекции отмечены синими и зелеными
пунктирными линиями. Пересечение
проекций преобразуют частоту согласно
(3). Так на рисунке 1 показано преобразование
нескольких точек исходного нормированного
ФНЧ в ФНЧ с заданной частотой среза
.
(верхний
правый график), а для преобразования
оси частот используют проекцию (3), как
это показано на нижнем левом графике.
Сами проекции отмечены синими и зелеными
пунктирными линиями. Пересечение
проекций преобразуют частоту согласно
(3). Так на рисунке 1 показано преобразование
нескольких точек исходного нормированного
ФНЧ в ФНЧ с заданной частотой среза
.
Например рассчитаем нормированный эллиптический ФНЧ, исходя из следующих начальных данных:
частота среза ;
частота
заграждения ![]()
неравномерность
в полосе пропускания ![]()
подавление
в полосе заграждения ![]()
Передаточная характеристика рассчитанного фильтра равна:
|
(4) |
Пересчитаем
полученную передаточную характеристику
в передаточную характеристику
эллиптического ФНЧ с частотой среза ![]() .
Для этого в выражение (4) сделаем
подстановку (2) получим:
.
Для этого в выражение (4) сделаем
подстановку (2) получим:
|
(5) |
На рисунках показаны АЧХ исходного нормированного ФНЧ и пересчитанного ФНЧ после частотного преобразования.
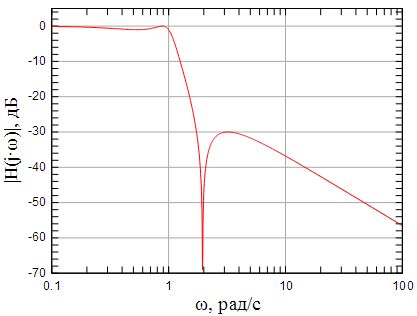
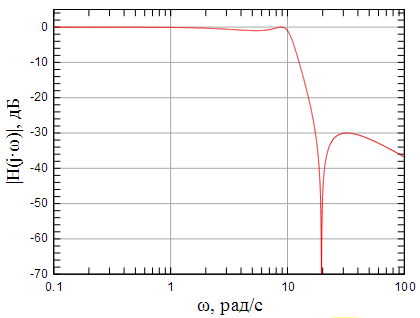
Рисунок 2: АЧХ исходного нормированного ФНЧ |
Рисунок 3: АЧХ пересчитанного ФНЧ с частотой среза 10 рад/с |
Расчет ФНЧ с заданной частотой среза на основе коридора АЧХ
Из рисунков 1 - 3 можно заметить, что неравномерность в полосе пропускания и уровень подавления в полосе заграждения не изменились, частота среза пересчитанного фильтра (рисунок 3) стала равна , но и переходная полоса тоже изменилась. АЧХ пересчитанного фильтра как бы «растянулась» до нужной частоты среза. При этом «растяжении» АЧХ, переходная полоса также растягивается, поэтому для расчета ФНЧ с заданной частотой среза и заданной переходной полосой необходимо рассчитывать передаточную характеристику ФНЧ по следующему правилу:
Шаг
1. Задаем частоту среза
и
частоту заграждения рассчитываемого
фильтра ![]()
Параметры коридора АЧХ нормированного ФНЧ задаются следующим образом:
|
(6) |
Шаг 2. Рассчитываем передаточную характеристику нормированного ФНЧ
Шаг 3. Осуществляем подстановку (2) и получаем искомую передаточную характеристику фильтра.
Например рассчитаем эллиптический ФНЧ исходя из следующих начальных данных:
частота среза ;
частота
заграждения ![]() ;
;
неравномерность в полосе пропускания ;
подавление
в полосе заграждения ![]() ;
;
Шаг 1. Рассчитываем коридор нормированного ФНЧ:
частота среза ;
частота
заграждения 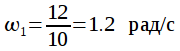 ;
;
неравномерность в полосе пропускания ;
подавление в полосе заграждения ;
Шаг 2. Рассчитываем передаточную характеристику нормированного ФНЧ. Получаем со следующими коэффициентами:
|
|
|
|
|
|
|
0.18601 |
0.0 |
0.28002 |
0.0 |
0.11727 |
0.0 |
0.01 |
|
|
|
|
|
|
|
0.20871 |
0.56518 |
1.43169 |
1.47989 |
2.23783 |
0.91544 |
1.00000 |
Шаг 3. Осуществляем подстановку (2):
|
(7) |
И получаем передаточную характеристику ФНЧ , рассчитанную по заданному коридору АЧХ. Коэффициенты передаточной характеристики приведены в таблицах:
|
|
|
|
|
|
|
186010.0 |
0.0 |
2800.2 |
0.0 |
11.727 |
0.0 |
0.01 |
|
|
|
|
|
|
|
208710.0 |
56518.0 |
14317.0 |
1479.9 |
223.78 |
9.1544 |
1.0 |
АЧХ исходного нормированного ФНЧ и ФНЧ после частотного преобразования показаны на рисунках 4 и 5.
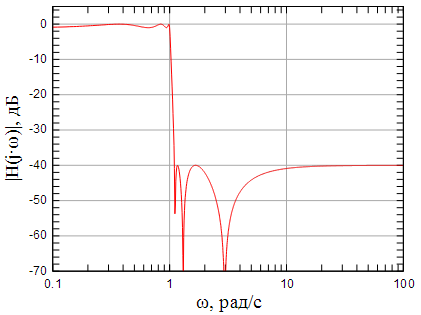
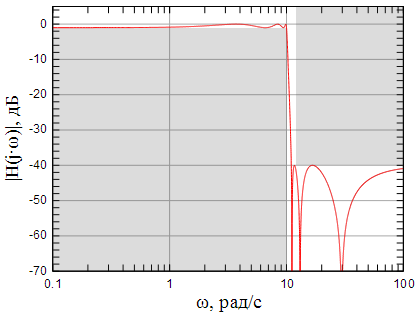
Рисунок 4: АЧХ исходного нормированного ФНЧ с пересчитанной переходной полосой |
Рисунок 5: АЧХ ФНЧ, рассчитанного по заданному коридору АЧХ |
Серым отмечен заданный коридор АЧХ рассчитываемого ФНЧ. Из рисунка 5 хорошо видно, что рассчитанный ФНЧ с частотой среза полностью укладывается в заданный коридор АЧХ.
Преобразование ФНЧ-ФВЧ
В данном разделе мы рассмотрим вопрос частотного преобразования нормированного ФНЧ в фильтр верхних частот с частотой среза , при сохранении неравномерности АЧХ в полосе пропускания и уровня подавления в полосе заграждения. Для частотного преобразования ФНЧ-ФВЧ применяют следующую подстановку:
|
(8) |
Как нетрудно заметить, подстановка (8) обратна подстановке (2), таким образом, частотное преобразование можно графически представить как это показано на рисунке 6.
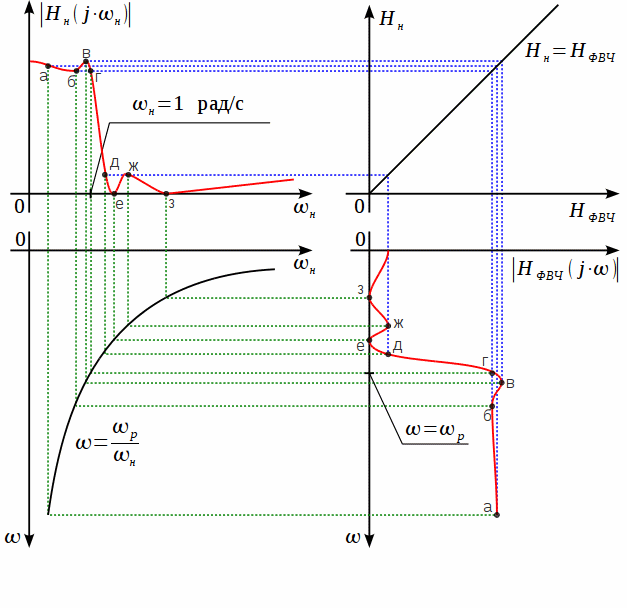 Рисунок
6: Графическое представление частотного
преобразования ФНЧ-ФВЧ
Рисунок
6: Графическое представление частотного
преобразования ФНЧ-ФВЧ
Как
и в случае преобразования ФНЧ-ФНЧ, на
верхнем левом графике показана АЧХ
исходного нормированного ФНЧ
,
а на нижнем правом — АЧХ после частотного
преобразования ![]() (повернутая
на 90 градусов). Для того, чтобы
неравномерность в полосе пропускания
и уровень подавления в полосе заграждения
пересчитанного фильтра были такими же
что и у исходного нормированного ФНЧ,
используют проекцию
(повернутая
на 90 градусов). Для того, чтобы
неравномерность в полосе пропускания
и уровень подавления в полосе заграждения
пересчитанного фильтра были такими же
что и у исходного нормированного ФНЧ,
используют проекцию ![]() (верхний
правый график), а для преобразования
оси частот используют проекцию, как это
показано на нижнем левом графике. Сами
проекции отмечены синими и зелеными
пунктирными линиями. Пересечение
проекций преобразуют частотную ось.
Так показано преобразование нескольких
точек исходного нормированного ФНЧ в
ФВЧ с заданной частотой среза
.
(верхний
правый график), а для преобразования
оси частот используют проекцию, как это
показано на нижнем левом графике. Сами
проекции отмечены синими и зелеными
пунктирными линиями. Пересечение
проекций преобразуют частотную ось.
Так показано преобразование нескольких
точек исходного нормированного ФНЧ в
ФВЧ с заданной частотой среза
.
Данное
преобразование является нелинейным,
так как ![]() ,
таким образом, нулевая частота исходного
нормированного ФНЧ переносится на
бесконечность, полоса нормированного
ФНЧ от 0 до 1 рад/с преобразуется в полосу
ФВЧ от
до
бесконечности, а полоса нормированного
ФНЧ от 1 рад/с до бесконечности рад/с
полностью размещается внутри полосы
от 0 до
пересчитанного
ФВЧ. Таким образом ось частот как бы
«выворачивается» относительно частоты
1 рад/с и переносится на
.
,
таким образом, нулевая частота исходного
нормированного ФНЧ переносится на
бесконечность, полоса нормированного
ФНЧ от 0 до 1 рад/с преобразуется в полосу
ФВЧ от
до
бесконечности, а полоса нормированного
ФНЧ от 1 рад/с до бесконечности рад/с
полностью размещается внутри полосы
от 0 до
пересчитанного
ФВЧ. Таким образом ось частот как бы
«выворачивается» относительно частоты
1 рад/с и переносится на
.
Например
преобразуем передаточную характеристику
эллиптического ФНЧ (4) в ФВЧ с частотой
среза
.
Произведем подстановку (8) и получим
передаточную характеристику ![]() :
:
|
(9) |
АЧХ исходного ФНЧ показана на рисунке 7 . На рисунке показана АЧХ ФВЧ с частотой среза полученного при помощи частотного преобразования (8).
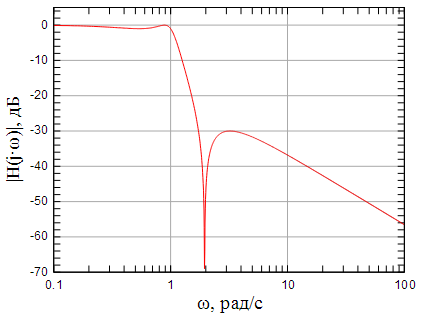
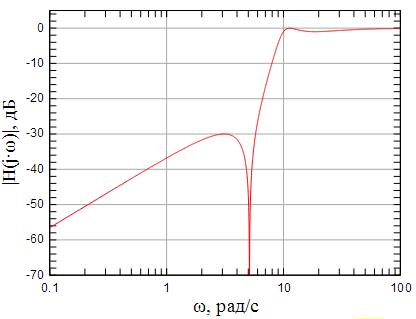
Рисунок 7: АЧХ исходного нормированного ФНЧ |
Рисунок 8: АЧХ пересчитанного ФВЧ с частотой среза |
Расчет ФВЧ с заданной частотой среза по заданному коридору АЧХ
При расчете ФВЧ, также как и в случае с ФНЧ, мы можем задать коридор АЧХ, как это показано на рисунке 9
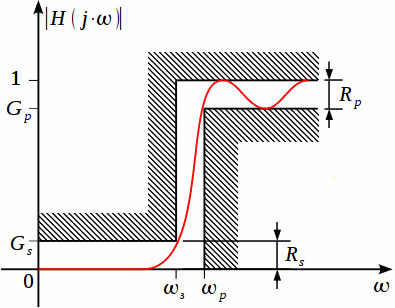 Рисунок
9: Коридор АЧХ для фильтра верхних частот
Рисунок
9: Коридор АЧХ для фильтра верхних частот
Для расчета ФВЧ по заданном коридору АЧХ необходимо исходный нормированный ФНЧ рассчитать исходя из следующих параметров:
|
(10) |
Обратите
внимание, что в отличии от ФНЧ, частота
среза фильтра верхних частот всегда
выше частоты заграждения![]() (смотри
рисунок 9), тогда при расчете нормированного
ФНЧ согласно (10)
(смотри
рисунок 9), тогда при расчете нормированного
ФНЧ согласно (10) ![]() .
.
Например рассчитаем эллиптический ФВЧ исходя из следующих начальных данных:
частота
среза ![]() ;
;
частота
заграждения ![]() ;
;
неравномерность в полосе пропускания ;
подавление в полосе заграждения .
Шаг 1. Рассчитываем коридор нормированного ФНЧ:
частота среза ;
частота
заграждения  ;
;
неравномерность в полосе пропускания ;
подавление в полосе заграждения .
Шаг 2. Рассчитываем передаточную характеристику нормированного ФНЧ. Получаем со следующими коэффициентами:
|
|
|
|
|
|
|
0.18601 |
0.0 |
0.28002 |
0.0 |
0.11727 |
0.0 |
0.01 |
|
|
|
|
|
|
|
0.20871 |
0.56518 |
1.43169 |
1.47989 |
2.23783 |
0.91544 |
1.00000 |
Шаг 3. Осуществляем подстановку (2):
|
(11) |
И получаем передаточную характеристику ФВЧ , рассчитанную по заданному коридору АЧХ. Коэффициенты передаточной характеристики приведены в таблицах:
|
|
|
|
|
|
|
29860 |
0.0 |
2431.6 |
0.0 |
40.323 |
0.0 |
0.18601 |
|
|
|
|
|
|
|
2986000 |
227790 |
46404 |
2557.2 |
206.16 |
6.7822 |
0.20871 |
АЧХ исходного нормированного ФНЧ и ФВЧ после частотного преобразования показаны на рисунках 10 и 11.
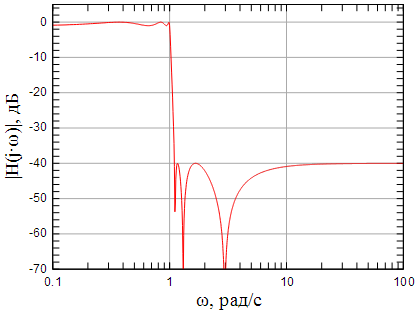
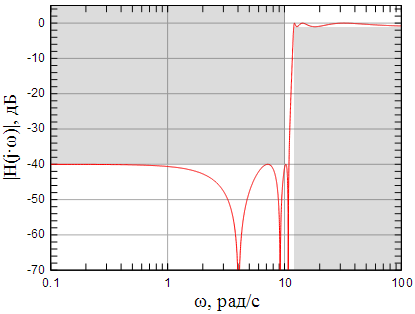
Рисунок 10: АЧХ исходного нормированного ФНЧ с пересчитанной переходной полосой |
Рисунок 11: АЧХ ФВЧ, рассчитанного по заданному коридору АЧХ |
Как видно из рисунка 11 рассчитанный ФВЧ полностью размещается в заданном коридоре АЧХ.
Таким образом мы рассмотрели в данной статье как преобразовать нормированный ФНЧ в ФНЧ с заданной частотой среза, а также в ФВЧ с заданной частотой среза. При этом важно подчеркнуть, что пересчет ФНЧ-ФНЧ и ФНЧ-ФВЧ не изменяет количества коэффициентов передаточной характеристики фильтра. В следующей статье мы рассмотрим оставшиеся два преобразования: ФНЧ — полосовой фильтр и ФНЧ — режекторный фильтр.
Частотное преобразование фильтров. Преобразование ФНЧ-ПФ и ФНЧ-РФ
Содержание
Введение
Частотное преобразование ФНЧ-ПФ
Расчет полосового фильтра по заданному коридору АЧХ
Пример расчета полосового фильтра по заданному коридору АЧХ
Частотное преобразование ФНЧ-РФ
Пример расчета режекторного фильтра по заданному коридору АЧХ
Выводы
Введение
В предыдущей статье мы рассмотрели вопрос частотного преобразования нормированного ФНЧ в ФНЧ с произвольной частотой среза, а также в фильтр верхних частот. В данной статье мы продолжим рассмотрение частотных преобразований аналоговых фильтров и приведем примеры преобразования ФНЧ — полосовой фильтр (ФНЧ-ПФ) и ФНЧ — режекторный фильтр (ФНЧ-РФ) по заданному коридору АЧХ.
Частотное преобразование ФНЧ-ПФ
Для начала рассмотрим коридор АЧХ для полосового фильтра (ПФ), представленный на рисунке 1.
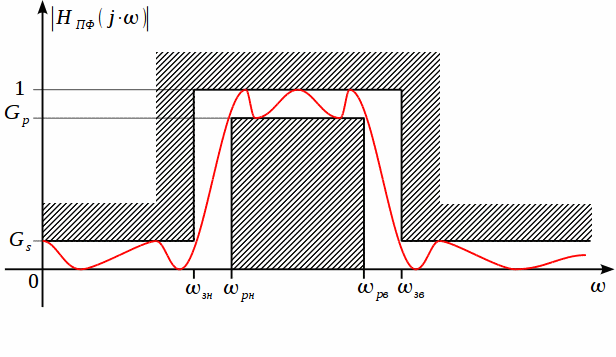 Рисунок
1: Коридор АЧХ полосового фильтра
Рисунок
1: Коридор АЧХ полосового фильтра
На
рисунке 1 обозначены: ![]() -
нижняя частота заграждения ПФ,
-
нижняя частота заграждения ПФ, ![]() -
нижняя частота пропускания ПФ,
-
нижняя частота пропускания ПФ, ![]() -
верхняя частота пропускания ПФ,
-
верхняя частота пропускания ПФ, ![]() -
верхняя частота заграждения ПФ, причем
-
верхняя частота заграждения ПФ, причем ![]() .
.
Преобразование нормированного ФНЧ в полосовой фильтр выполняется в виде постановки:
|
(1) |
При этом частотная ось нормированного ФНЧ связана с частотной осью ПФ соотношением:
|
(2) |
Обратите
внимание, что при пересчете используются
как положительные, так и отрицательные
частоты
комплексного
коэффициента передачи ![]() .
.
Также
можно заметить, если ![]() ,
то согласно (2),
,
то согласно (2), ![]() ,
т.е. нулевая частота исходного
нормированного ФНЧ преобразуется в
частоту
,
т.е. нулевая частота исходного
нормированного ФНЧ преобразуется в
частоту ![]() .
Если
.
Если ![]() то
согласно (2),
то
согласно (2), ![]() ,
а если
,
а если ![]() ,
то
,
то ![]() .
Таким образом, вся отрицательная полуось
частот нормированного ФНЧ преобразуется
в интервал от 0 до
полосового
фильтра, а положительная полуось частот
нормированного ФНЧ преобразуется в
интервал от
до
бесконечности. Графически частотное
преобразование ФНЧ-ПФ показано на
рисунке 2.
.
Таким образом, вся отрицательная полуось
частот нормированного ФНЧ преобразуется
в интервал от 0 до
полосового
фильтра, а положительная полуось частот
нормированного ФНЧ преобразуется в
интервал от
до
бесконечности. Графически частотное
преобразование ФНЧ-ПФ показано на
рисунке 2.
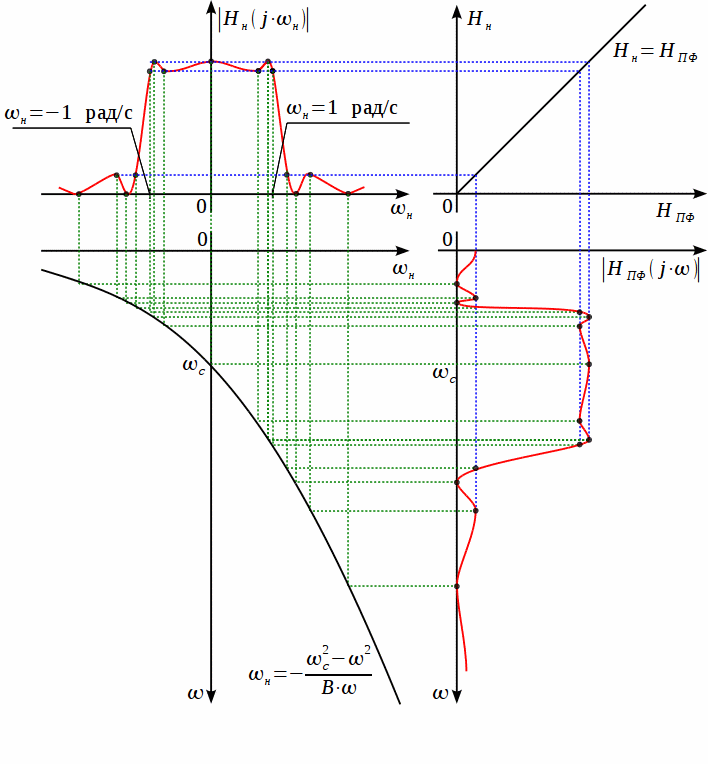 Рисунок
2: Графическое представление преобразования
ФНЧ-ПФ
Рисунок
2: Графическое представление преобразования
ФНЧ-ПФ
На
верхнем левом графике показана АЧХ
исходного нормированного ФНЧ
для
положительных и отрицательных
частот
(поскольку
коэффициенты передаточной функции
нормированного ФНЧ чисто вещественны,
то
симметрично
относительно нуля). Поскольку требуется
оставить без изменения уровни подавления
в полосе заграждения и неравномерность
в полосе пропускания пересчитанного
фильтра, то используется проекция![]() (верхний
правый график, проекции отображены
синей пунктирной линией). Преобразование
частоты согласно (2) показано на нижнем
левом графике (линии проекции отображены
зеленой пунктирной линией). На правом
нижнем графике показана АЧХ пересчитанного
ПФ, повернутая на 90 градусов, полученная
в результате пересечения линий проекции.
(верхний
правый график, проекции отображены
синей пунктирной линией). Преобразование
частоты согласно (2) показано на нижнем
левом графике (линии проекции отображены
зеленой пунктирной линией). На правом
нижнем графике показана АЧХ пересчитанного
ПФ, повернутая на 90 градусов, полученная
в результате пересечения линий проекции.
Сделаем
важное замечание. Если некоторая
частота ![]() преобразуется
согласно (2) в частоту
,
а частота
преобразуется
согласно (2) в частоту
,
а частота ![]() в
частоту
в
частоту ![]() ,
то можно записать:
,
то можно записать:
|
(3) |
откуда
|
(4) |
Таким
образом мы получили, что симметричные
относительно
точки
АЧХ исходного нормированного ФНЧ
преобразуются в точки с геометрической
симметрией относительно частоты
(термин
геометрическая симметрия означает,
что ![]() ,
т.е.
,
т.е. ![]() есть
среднее геометрическое
есть
среднее геометрическое ![]() и
).
Это крайне важное свойство частотного
преобразования ФНЧ-ПФ, которое мы будем
использовать в дальнейшем.
и
).
Это крайне важное свойство частотного
преобразования ФНЧ-ПФ, которое мы будем
использовать в дальнейшем.
Расчет полосового фильтра по заданному коридору АЧХ
Геометрическая симметрия полученного ПФ относительно позволяет нам произвести пересчет частоты заграждения аналогового нормированного ФНЧ таким образом, что при нелинейном преобразовании оси частот согласно выражению (2) АЧХ полученного ПФ полностью укладывалась в заданный коридор АЧХ. До этого мы не накладывали никаких ограничений на частоты коридора АЧХ ПФ, а значит они могут быть выбраны произвольно лишь бы выполнялось условие . В случае с ФНЧ и ФВЧ у нас всегда была переходная полоса, которая задавала частоту заграждения нормированного ФНЧ, в случае с ПФ таких переходных полос две, и если даже мы удовлетворяем одной из этих двух переходных полос, то нет никакой гарантии, что мы удовлетворяем и второй. Поэтому прежде всего мы должны выработать правило выбора переходной полосы на основе которой мы будем производить пересчет коридора для исходного нормированного ФНЧ. Для этого рассмотрим рисунок 3.
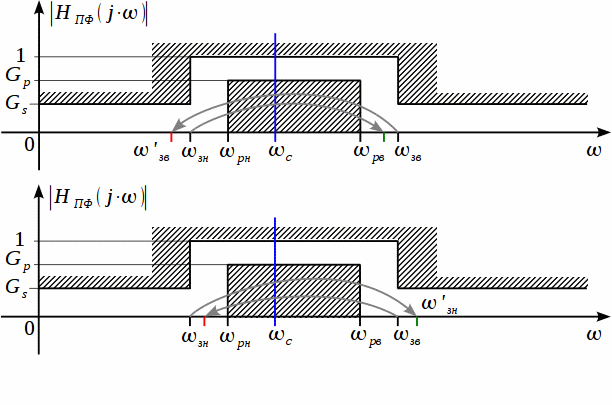 Рисунок
3: Выбор переходной полосы пересчета
частоты заграждения
Рисунок
3: Выбор переходной полосы пересчета
частоты заграждения
Мы
произвольно задали
,
рассчитали частоту
согласно
выражению
.
Теперь воспользовавшись правилом
геометрической симметрии мы можем
проверить куда относительно нижней
частоты заграждения ![]() попадает
частота
попадает
частота ![]() симметричная
верхней частоты заграждения
(на
рисунке 3
отмечена
красным цветом):
симметричная
верхней частоты заграждения
(на
рисунке 3
отмечена
красным цветом):
|
(5) |
На
рисунке 3 показано два варианта:
первый ![]() (верхний
график рисунка 3), это означает, что если
мы возьмем для расчета верхнюю переходную
полосу, то полученная АЧХ не удовлетворит
нижней переходной полосе ввиду свойства
симметрии, и надо пересчет вести по
нижней переходной полосе; второй вариант
(нижний график рисунка 3)
(верхний
график рисунка 3), это означает, что если
мы возьмем для расчета верхнюю переходную
полосу, то полученная АЧХ не удовлетворит
нижней переходной полосе ввиду свойства
симметрии, и надо пересчет вести по
нижней переходной полосе; второй вариант
(нижний график рисунка 3) ![]() говорит
о том, что выбрав верхнюю переходную
полосу мы одновременно и удовлетворим
нижней переходной полосе. Таким образом
мы можем выбрать по какой переходной
полосе вести пересчет частоты заграждения
нормированного ФНЧ. Тогда частоту
заграждения нормированного ФНЧ, можно
рассчитать из выражения:
говорит
о том, что выбрав верхнюю переходную
полосу мы одновременно и удовлетворим
нижней переходной полосе. Таким образом
мы можем выбрать по какой переходной
полосе вести пересчет частоты заграждения
нормированного ФНЧ. Тогда частоту
заграждения нормированного ФНЧ, можно
рассчитать из выражения:
|
(6) |
Рассмотрим
пример. Пусть ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
тогда пересчитываем
:
,
тогда пересчитываем
:
|
(7) |
Тогда
пересчет частоты заграждения нормированного
ФНЧ будем вести при ![]() и
получим:
и
получим:
|
(8) |
Рассмотрим
второй пример. Пусть теперь коридор АЧХ
ПФ задан с такими параметрами:
,
,![]() и
и ![]() ,
тогда пересчитываем
:
,
тогда пересчитываем
:
|
(9) |
Тогда
пересчет частоты заграждения нормированного
ФНЧ будем вести при ![]() и
получим:
и
получим:
|
(10) |
Таким образом мы рассмотрели вопрос пересчета частоты заграждения нормированного ФНЧ для удовлетворения заданного коридора АЧХ полосового фильтра. Рассмотрим пример расчета ПФ по заданному коридору АЧХ.
Пример расчета полосового фильтра по заданному коридору АЧХ
Приведем окончательно порядок расчета ПФ по заданному коридору АЧХ на конкретном примере. Пусть нам требуется рассчитать полосовой эллиптический фильтр, причем коридор АЧХ задан следующим образом:
Нижняя
частота заграждения:![]() ;
;
Нижняя
частота пропускания:![]() ;
;
Верхняя
частота пропускания:![]() ;
;
Верхняя
частота заграждения:![]() ;
;
Неравномерность
в полосе пропускания: ![]() ;
;
Уровень
подавления в полосе заграждения: ![]() .
.
Шаг
1. Рассчитываем частоту геометрической
симметрии
АЧХ
и полосу пропускания ![]() полосового
фильтра согласно (1):
полосового
фильтра согласно (1):
|
(11) |
Шаг 2. Пересчитываем полосу заграждения нормированного эллиптического ФНЧ. Для этого проверяем согласно (5):
|
(12) |
Тогда в выражение (6) подставляем и получим:
|
(13) |
Шаг
3. Рассчитываем нормированный эллиптический
ФНЧ по следующему коридору АЧХ: частота
среза
,
частота заграждения ![]() ,
неравномерность в полосе пропускания
и
подавление в полосе заграждения
.
Передаточная характеристика нормированного
ФНЧ, рассчитанная по заданному коридору
АЧХ (как рассчитывается эллиптический
фильтр смотри здесь)
имеет вид:
,
неравномерность в полосе пропускания
и
подавление в полосе заграждения
.
Передаточная характеристика нормированного
ФНЧ, рассчитанная по заданному коридору
АЧХ (как рассчитывается эллиптический
фильтр смотри здесь)
имеет вид:
|
(14) |
Шаг 4. Осуществляем подстановку:
|
(15) |
И получаем передаточную характеристику полосового фильтра с коэффициентами числителя и знаменателя приведенными в таблице:
|
|
|
|
|
|
|
|
|
|
|
0.0 |
1.4862e+7 |
0.0 |
2.0305e+6 |
0.0 |
71846 |
0.0 |
360.97 |
0.0 |
0.469721 |
0.0 |
|
|
|
|
|
|
|
|
|
|
|
2.373e+9 |
2.9217e+8 |
2.3613e+8 |
2.1934e+7 |
7.9269e+6 |
5.0402e+5 |
1.0569e+5 |
3899.4 |
559.71 |
9.2340 |
1.0 |
Обратите
внимание, что при преобразовании ФНЧ-ПФ
количество коэффициентов передаточной
функции увеличивается, и максимальные
степени полиномов числителя и знаменателя
ПФ в 2 раза выше чем степени нормированного
ФНЧ. Это связано с тем что подстановка
содержит ![]() .
Теперь нужно сделать одно важное
замечание. Когда мы вводили понятие
порядка фильтра, мы говорили о том, что
порядок фильтра равен максимальной
степени полинома числителя или знаменателя
фильтра, но это относилось к ФНЧ. Для ПФ
порядок в 2 раза ниже максимальной
степени полиномов числителя и знаменателя.
Так в нашем примере порядок ПФ равен 5
(как и порядок нормированного ФНЧ), а
максимальная степень полиномов равна
10. Поэтому если идет речь о том, что
необходимо рассчитать ПФ 7-го порядка,
то это означает, что нормированный ФНЧ
должен быть 7-го порядка, а полиномы
числителя и знаменателя ПФ будут иметь
степень 14, а количество коэффициентов
передаточной характеристики полосового
фильтра 7-го порядка будет равно 15. На
рисунках 4 и 5 показаны АЧХ нормированного
ФНЧ (14), а также полученного полосового
фильтра, коэффициенты передаточной
функции которого приведены в таблицах
выше.
.
Теперь нужно сделать одно важное
замечание. Когда мы вводили понятие
порядка фильтра, мы говорили о том, что
порядок фильтра равен максимальной
степени полинома числителя или знаменателя
фильтра, но это относилось к ФНЧ. Для ПФ
порядок в 2 раза ниже максимальной
степени полиномов числителя и знаменателя.
Так в нашем примере порядок ПФ равен 5
(как и порядок нормированного ФНЧ), а
максимальная степень полиномов равна
10. Поэтому если идет речь о том, что
необходимо рассчитать ПФ 7-го порядка,
то это означает, что нормированный ФНЧ
должен быть 7-го порядка, а полиномы
числителя и знаменателя ПФ будут иметь
степень 14, а количество коэффициентов
передаточной характеристики полосового
фильтра 7-го порядка будет равно 15. На
рисунках 4 и 5 показаны АЧХ нормированного
ФНЧ (14), а также полученного полосового
фильтра, коэффициенты передаточной
функции которого приведены в таблицах
выше.
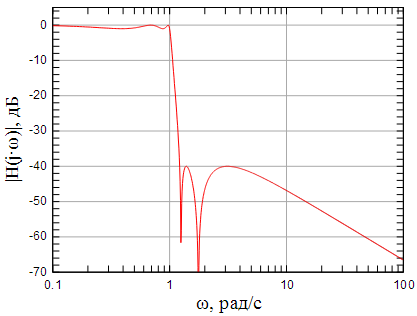
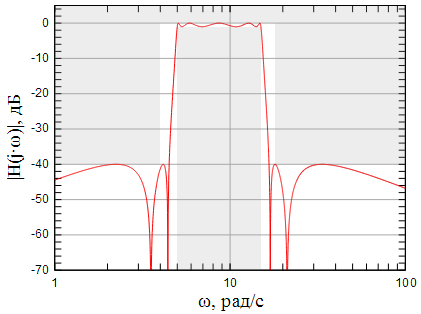
Рисунок 4: АЧХ нормированного ФНЧ |
Рисунок 5: АЧХ рассчитанного полосового фильтра |
Как можно заметить из рисунка 5, АЧХ полученного полосового фильтра полностью укладывается в заданный коридор.
Частотное преобразование ФНЧ-РФ
Нам осталось рассмотреть лишь одно преобразование передаточных характеристик, а именно ФНЧ - режекторный фильтр (ФНЧ-РФ). Коридор АЧХ для режекторного фильтра показан на рисунке 6.
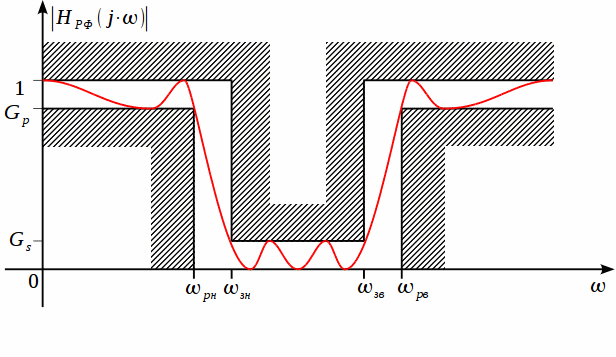 Рисунок
6: Коридор АЧХ режекторного фильтра
Рисунок
6: Коридор АЧХ режекторного фильтра
Как
и полосовой фильтр, РФ имеет две переходные
полосы, причем в отличии от ПФ, частоты
коридора АЧХ режекторного фильтра
удовлетворяют следующему правилу: ![]() ,
т.е. верхняя и нижняя частоты заграждения
находятся рядом, а верхняя и нижняя
частоты пропускания по краям.
,
т.е. верхняя и нижняя частоты заграждения
находятся рядом, а верхняя и нижняя
частоты пропускания по краям.
Преобразования фильтра нижних частот в режекторный фильтр осуществляется при помощи подстановки:
|
(16) |
Видно что данная подстановка обратна преобразованию ФНЧ-ПФ.
При этом частотная ось ФНЧ связана с частотной осью РФ соотношением:
|
(17) |
Обратите
внимание, что при пересчете используются
как положительные, так и отрицательные
частоты
комплексного
коэффициента передачи
.
Также можно заметить, если
,
то согласно (17),
,
или
т.е.
нулевая частота исходного ФНЧ «расходится»
на 0 и на бесконечность. Если ![]() то
согласно (17),
.
Таким образом, вся отрицательная полуось
частот исходного ФНЧ преобразуется в
интервал от 0 до
режекторного
фильтра, а положительная полуось частот
нормированного ФНЧ преобразуется в
интервал от
до
бесконечности. При этом полуоси исходного
ФНЧ как бы «выворачиваются», т.е. нулевая
частота
«раздваивается»
и расходится на бесконечность
и
,
а частоты разнесенные на
бесконечность
сходятся
в точке
.
Графически частотное преобразование
ФНЧ-РФ показано на рисунке 7.
то
согласно (17),
.
Таким образом, вся отрицательная полуось
частот исходного ФНЧ преобразуется в
интервал от 0 до
режекторного
фильтра, а положительная полуось частот
нормированного ФНЧ преобразуется в
интервал от
до
бесконечности. При этом полуоси исходного
ФНЧ как бы «выворачиваются», т.е. нулевая
частота
«раздваивается»
и расходится на бесконечность
и
,
а частоты разнесенные на
бесконечность
сходятся
в точке
.
Графически частотное преобразование
ФНЧ-РФ показано на рисунке 7.
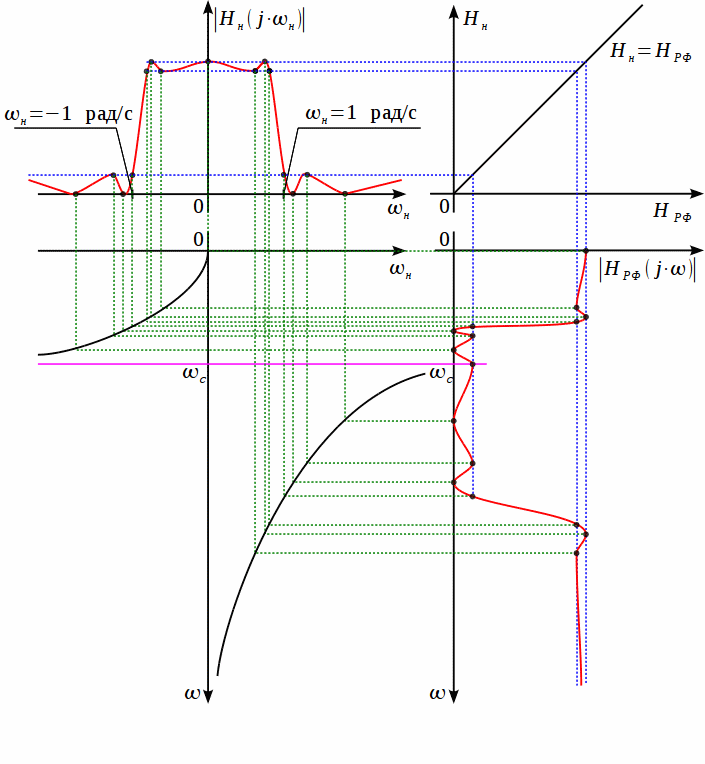 Рисунок
7: Графическое представление преобразования
ФНЧ-РФ
Рисунок
7: Графическое представление преобразования
ФНЧ-РФ
Крайне
важно заметить, что исходный ФНЧ не
является нормированным, т.е. его частота
среза не равна единицы, а меньше, так
как на частоте ![]() ФНЧ
должен обеспечивать заданный уровень
подавления.
ФНЧ
должен обеспечивать заданный уровень
подавления.
Как и в случае с полосовым фильтром, частотная характеристика преобразованного режекторного фильтра обладает геометрической симметрией относительно частоты . Действительно, возьмем две произвольные частоты, расположенные симметрично относительно нуля в АЧХ исходного ФНЧ и , тогда согласно (17) этим частотам после преобразования будут соответствовать некоторые частоты режекторного фильтра:
|
(18) |
Тогда можно приравнять:
|
(19) |
При
произвольном задании частот коридора
АЧХ режекторного фильтра (рисунок 6), мы
должны так выбрать частоту среза
исходного ФНЧ (напомним еще раз, что при
расчете режекторного фильтра мы
зафиксировали частоту заграждения
исходного ФНЧ
,
а значит должны задавать именно частоту
среза ![]() ),
при которой пересчитанный РФ будет
удовлетворять заданному коридору АЧХ.
Для задания частоты среза
исходного
ФНЧ необходимо, произвести анализ по
аналогии с тем, что мы делали при расчете
ПФ. А именно рассчитаем симметричные
частоты для верхней и нижней частот
среза РФ:
),
при которой пересчитанный РФ будет
удовлетворять заданному коридору АЧХ.
Для задания частоты среза
исходного
ФНЧ необходимо, произвести анализ по
аналогии с тем, что мы делали при расчете
ПФ. А именно рассчитаем симметричные
частоты для верхней и нижней частот
среза РФ:
|
(20) |
После
этого необходимо сделать выбор: если ![]() ,
тогда пересчет частоты среза исходного
ФНЧ осуществлять на основе верхней
частоты среза по формуле:
,
тогда пересчет частоты среза исходного
ФНЧ осуществлять на основе верхней
частоты среза по формуле:
|
(21) |
В
противном случае (если ![]() ),
то пересчет осуществлять по нижней
частоте среза РФ:
),
то пересчет осуществлять по нижней
частоте среза РФ:
|
(22) |
Рассмотрим
пример. Пусть частоты коридора АЧХ РФ
заданы следующими значениями: ![]() ,
, ![]() ,
, ![]() и
и ![]() .
Произведем пересчет частоты среза
исходного ФНЧ. Для этого предварительно
рассчитаем частоту
.
Произведем пересчет частоты среза
исходного ФНЧ. Для этого предварительно
рассчитаем частоту ![]() .
Рассчитываем симметричные частоты
согласно (20):
.
Рассчитываем симметричные частоты
согласно (20):
|
(23) |
Получили,
что ![]() ,
и значит, что пересчет частоты среза
ФНЧ надо вести по формуле (22), так как
при этом
,
и значит, что пересчет частоты среза
ФНЧ надо вести по формуле (22), так как
при этом![]() и
АЧХ полученного фильтра полностью
уложится в заданный коридор. Рассчитаем
частоту среза исходного ФНЧ согласно
(22), при учете, что
и
АЧХ полученного фильтра полностью
уложится в заданный коридор. Рассчитаем
частоту среза исходного ФНЧ согласно
(22), при учете, что ![]() :
:
|
(24) |
Обратите внимание, что частота среза полученного ФНЧ меньше единицы.
Таким образом, порядок расчета режекторного фильтра по заданному коридору АЧХ можно окончательно представить следующим образом:
Шаг 1. Выбор переходной полосы, по которой производить пересчет коридора АЧХ для ФНЧ по рассмотренному выше правилу и расчет частоты среза ФНЧ согласно (21) или (22).
Шаг 2. Расчет ФНЧ по заданному коридору АЧХ, полученному в шаге 1. Параметры неравномерности в полосе пропускания и уровня подавления в полосе заграждения принимаются такие же что и у режекторного фильтра.
Шаг 3. При помощи частотного преобразования производим пересчет частотной характеристики ФНЧ в РФ согласно (16).
Пример расчета режекторного фильтра по заданному коридору АЧХ
Пусть необходимо рассчитать эллиптический режекторный фильтр, заданный следующим коридором АЧХ
нижняя частота среза ;
нижняя частота заграждения ;
верхняя частота заграждения ;
верхняя частота среза ;
неравномерность в полосе пропускания ;
уровень подавления в полосе заграждения .
Шаг
1. Был подробно рассмотрен в примере
выше. Получили частоту среза ФНЧ равную ![]() .
.
Шаг2. Расчет ФНЧ по следующему коридору АЧХ:
частота
среза ![]()
частота заграждения
неравномерность в полосе пропускания
уровень подавления в полосе заграждения
Передаточная характеристика ФНЧ, удовлетворяющая заданному коридору имеет вид:
|
(25) |
При расчете передаточной характеристики ФНЧ применялось преобразование нормированного ФНЧ в ФНЧ с частотой среза (смотри предыдущую статью).
Шаг 3. Применяем подстановку :
|
(26) |
В результате численной подстановки получим передаточную функцию режекторного фильтра, коэффициенты которой представлены в таблице:
|
|
|
|
|
|
|
|
|
122330 |
0.0 |
12355 |
0.0 |
430.85 |
0.0 |
6.1013 |
0.0 |
0.02983 |
|
|
|
|
|
|
|
|
|
137260 |
49199 |
27130 |
4772.2 |
1326.2 |
106.05 |
13.397 |
0.53991 |
0.03347 |
Обратите внимание, что при преобразовании ФНЧ-РФ количество коэффициентов передаточной функции, как и в случае с преобразованием ФНЧ-ПФ увеличивается, и максимальные степени полиномов числителя и знаменателя РФ в 2 раза выше чем степени исходного ФНЧ. Это связано с тем что подстановка содержит . Как и в случае с ПФ порядок РФ определяется порядком исходного ФНЧ, а не степенью полиномов числителя и знаменателя. Так в нашем примере порядок РФ равен 4 (как и порядок нормированного ФНЧ), а максимальная степень полиномов равна 8. Поэтому если идет речь о том, что необходимо рассчитать РФ 7-го порядка, то это означает, что нормированный ФНЧ должен быть 7-го порядка, а полиномы числителя и знаменателя ПФ будут иметь степень 14. На рисунках 8 и 9 показаны АЧХ исходного ФНЧ, а также полученного режекторного фильтра (коэффициенты передаточной функции приведены в таблицах выше).
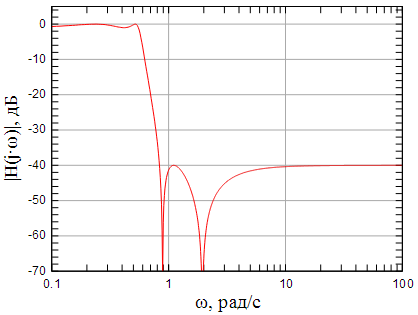
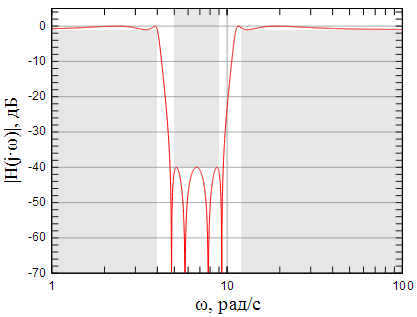
Рисунок 8: АЧХ исходного ФНЧ для расчета РФ |
Рисунок 9: АЧХ режекторного фильтра, рассчитанного по заданному коридору АЧХ |
Как видно из рисунка рассчитанный РФ полностью размещается в заданном коридоре АЧХ.
Для программной реализации всех частотных преобразований используют алгоритм дробно-рациональной подстановки, подробно рассмотренный здесь.
Выводы
Таким образом мы рассмотрели расчет полосового и режекторного фильтров по заданному коридору АЧХ на основе частотного преобразования ФНЧ. Было показано, что АЧХ ПФ и РФ обладают свойством геометрической симметрии, кроме того порядок полиномов числителя и знаменателя передаточной функции после частотного преобразования удваивается по сравнению с исходным ФНЧ.
Билинейное преобразование. Этапы проектирования цифрового фильтра.
Df Структуры цифровых фильтров и их характеристики
Содержание
Введение
Основные обозначения
Структурная схема КИХ-фильтра
Структурные схемы БИХ-фильтра. Прямая и каноническая формы БИХ-фильтра
Характеристики цифровых фильтров
Выводы
Введение
Ранее мы рассмотрели разностные уравнения цифровых фильтров в виде:
|
(1) |
где ![]() -
отсчеты на выходе фильтра,
-
отсчеты на выходе фильтра, ![]() - входные
отсчеты,
- входные
отсчеты, ![]() и
и ![]() -
коэффициенты числителя и знаменателя
передаточной характеристики фильтра
соответственно. Также мы говорили о
том, что если все коэффициенты
кроме
равны
нулю, то такой фильтр называется
КИХ-фильтром, а если хотя бы один
коэффициент
помимо
отличен
от нуля, то такой фильтр называется
БИХ-фильтр.
-
коэффициенты числителя и знаменателя
передаточной характеристики фильтра
соответственно. Также мы говорили о
том, что если все коэффициенты
кроме
равны
нулю, то такой фильтр называется
КИХ-фильтром, а если хотя бы один
коэффициент
помимо
отличен
от нуля, то такой фильтр называется
БИХ-фильтр.
В данной статье мы рассмотрим структурные схемы цифровых фильтров и их характеристики.
Основные обозначения
Согласно
выражению (1), сигнал на выходе фильтра
зависит от задержанного входного
сигнала, а также от предыдущих отсчетов
на выходе, поэтому для реализации фильтра
нам потребуются линии задержки. Вспомним,
что согласно z-преобразованию, задержка
на один отсчет соответствует умножению
образа на ![]() .
Также нам потребуются умножители на
постоянные коэффициенты
и
и
сумматоры. На рисунке 1 показаны
обозначения основных блоков для
построения цифрового фильтра.
.
Также нам потребуются умножители на
постоянные коэффициенты
и
и
сумматоры. На рисунке 1 показаны
обозначения основных блоков для
построения цифрового фильтра.
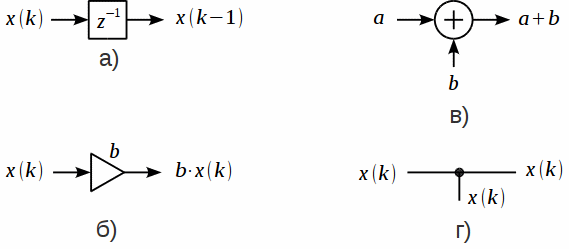 Рисунок
1: Обозначения блоков цифрового фильтра
Рисунок
1: Обозначения блоков цифрового фильтра
На рисунке 1 а) обозначена линия задержки, 1 б) умножитель на константу, 1 в) сумматор и 1 г) разветвление.
Структурная схема КИХ-фильтра
Разностное уравнение КИХ фильтра не содержит рекурсивной части:
|
(2) |
Выражение
(2) получается из выражения (1) при ![]() и
и ![]() .
.
Структурная схема нерекурсивного КИХ-фильтра показана на рисунке 2.
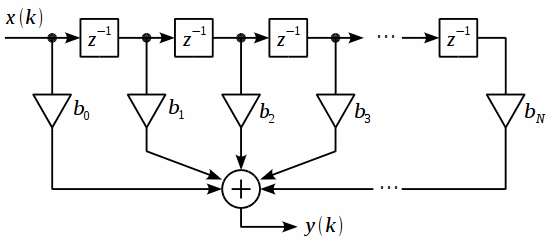 Рисунок
2: Структурная схема нерекурсивного
КИХ-фильтра
Рисунок
2: Структурная схема нерекурсивного
КИХ-фильтра
КИХ
фильтр порядка
содержит
линий
задержки и ![]() коэффициент.
Если коэффициент
коэффициент.
Если коэффициент ![]() ,
то получим КИХ фильтр порядка
у
которого умножение на
будет
тривиальным. Импульсная характеристика
КИХ-фильтра всегда конечна и полностью
совпадает с коэффициентами фильтра.
,
то получим КИХ фильтр порядка
у
которого умножение на
будет
тривиальным. Импульсная характеристика
КИХ-фильтра всегда конечна и полностью
совпадает с коэффициентами фильтра.
Структурные схемы БИХ-фильтра. Прямая и каноническая формы БИХ-фильтра
При построении БИХ-фильтра перепишем уравнение (1) к виду:
|
(3) |
В
выражении (3) можно выделить нерекурсивную
составляющую ![]() и
рекурсивную
и
рекурсивную ![]() .
Тогда БИХ-фильтр можно представить как
сумму нерекурсивной и рекурсивной
составляющих, как это показано на рисунке
3.
.
Тогда БИХ-фильтр можно представить как
сумму нерекурсивной и рекурсивной
составляющих, как это показано на рисунке
3.
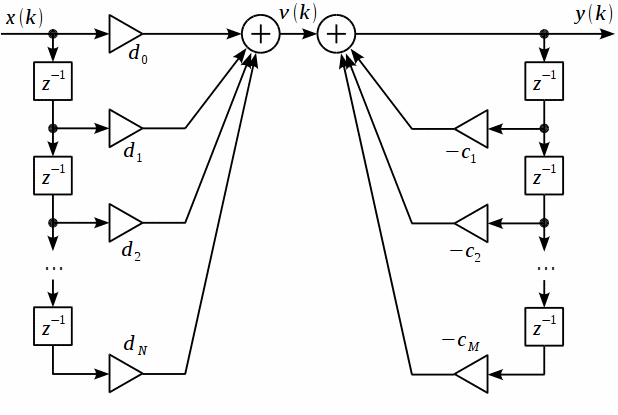 Рисунок
3: Прямая форма БИХ-фильтра
Рисунок
3: Прямая форма БИХ-фильтра
Такое
представление БИХ-фильтра называют
прямой формой реализации. Обратим
внимание, что количество линий задержек
БИХ-фильтра равно ![]() ,
что больше чем количество линий задержек
КИХ-фильтра того же порядка (напомним,
что порядок БИХ-фильтра равен максимальной
степени полинома числителя или знаменателя
передаточной характеристики фильтра).
При этом также обратим внимание, что
БИХ фильтр представляет собой каскадное
соединение нерекурсивной и рекурсивной
частей, которые можно поменять местами.
Тогда получим структуру, показанную на
рисунке 4.
,
что больше чем количество линий задержек
КИХ-фильтра того же порядка (напомним,
что порядок БИХ-фильтра равен максимальной
степени полинома числителя или знаменателя
передаточной характеристики фильтра).
При этом также обратим внимание, что
БИХ фильтр представляет собой каскадное
соединение нерекурсивной и рекурсивной
частей, которые можно поменять местами.
Тогда получим структуру, показанную на
рисунке 4.
 Рисунок
4: Перестановка нерекурсивной и рекурсивной
составляющих БИХ-фильтра
Рисунок
4: Перестановка нерекурсивной и рекурсивной
составляющих БИХ-фильтра
Объединив линии задержки в структуре, показанной на рисунке 4, получим каноническую форму БИХ-фильтра, представленную на рисунке 5.
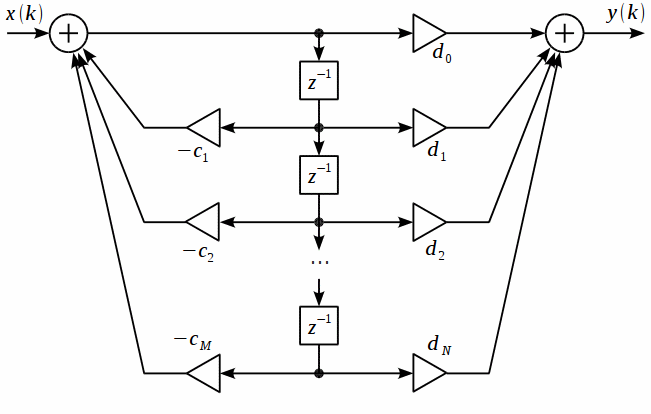 Рисунок
5: Каноническая форма БИХ-фильтра
Рисунок
5: Каноническая форма БИХ-фильтра
В канонической форме БИХ-фильтра количество линий задержек всегда равно порядку фильтра.
Характеристики цифровых фильтров
Ранее мы
уже говорили, что цифровой фильтр
задается свой передаточной характеристикой ![]() ,
которая представляет отношение
z-образов
,
которая представляет отношение
z-образов ![]() выходного
сигнала ко входному
выходного
сигнала ко входному ![]() :
:
|
(4) |
При
этом мы
уже знаем,
что z-преобразование мы получили путем
отображения комплексной s-плоскости
вида![]() где
где ![]() -
период дискретизации исходного сигнала
и импульсной характеристики фильтра.
Без потери общности можно принять
-
период дискретизации исходного сигнала
и импульсной характеристики фильтра.
Без потери общности можно принять ![]() ,
тогда
,
тогда ![]() Тогда
подставив в передаточную характеристику
дискретного фильтра (4)
Тогда
подставив в передаточную характеристику
дискретного фильтра (4) ![]() ,
мы получим передаточную характеристику
фильтра по Лапласу, из которой можно
получить комплексный коэффициент
передачи дискретного фильтра путем
подстановки
.
Таким образом, комплексный коэффициент
передачи цифрового фильтра обозначается
как
,
мы получим передаточную характеристику
фильтра по Лапласу, из которой можно
получить комплексный коэффициент
передачи дискретного фильтра путем
подстановки
.
Таким образом, комплексный коэффициент
передачи цифрового фильтра обозначается
как ![]() и
равен:
и
равен:
|
(5) |
Амплитудно-частотная характеристика (АЧХ) цифрового фильтра может быть получена как модуль , а фазочастотная (ФЧХ) как аргумент:
|
(6) |
Также вводят понятие групповой задержки как производной от ФЧХ:
|
(7) |
Обратите
внимание, что АЧХ и ФЧХ и групповая
задержка цифрового фильтра есть
непрерывные функции частоты. При этом
согласно (5)
периодическая
функция с периодом ![]() ,
так как
,
так как ![]() .
Последнее равенство не вызывает сомнений,
если подставить его в выражение (5). Таким
образом, характеристику цифрового
фильтра достаточно проанализировать
на интервале
.
Последнее равенство не вызывает сомнений,
если подставить его в выражение (5). Таким
образом, характеристику цифрового
фильтра достаточно проанализировать
на интервале ![]() .
.
Цифровой
фильтр также определяется своей
импульсной характеристикой, преобразование
Фурье от которой дает комплексный
коэффициент передачи. Если комплексный
коэффициент передачи — периодическая
функция частоты, то импульсная
характеристика ![]() дискретного
фильтра определяется как разложение в
ряд Фурье
:
дискретного
фильтра определяется как разложение в
ряд Фурье
:
|
(8) |
Рассчитывать импульсную характеристику через интеграл не совсем удобно, кроме того количество отсчетов импульсной характеристики БИХ-фильтра бесконечно, и все их рассчитать невозможно. Однако, если фильтр устойчивый, то убывает, с увеличением , и можно рассчитать заданное количество отсчетов импульсной характеристики фильтра при помощи быстрого преобразования Фурье (FFT).
Пусть требуется рассчитать первых отсчетов импульсной характеристики фильтра, заданного передаточной характеристикой
Первое,
что мы должны сделать — рассчитать
комплексный коэффициент передачи
заданного фильтра. Для численного
расчета необходимо задать сетку
частот ![]()
![]()
![]() .
Тогда на данной сетке частот рассчитаем
комплексный коэффициент передачи
.
Тогда на данной сетке частот рассчитаем
комплексный коэффициент передачи ![]() ,
таким образом, получим
отсчетов
комплексного коэффициента передачи
фильтра. После этого можно рассчитать
импульсную характеристику как
,
таким образом, получим
отсчетов
комплексного коэффициента передачи
фильтра. После этого можно рассчитать
импульсную характеристику как ![]() ,
где
,
где ![]() -
оператор обратного быстрого преобразования
Фурье. Таким образом, мы рассчитали
характеристики фильтра с заданной
передаточной характеристикой. Данный
путь расчета приводил к комплексному
коэффициенту передачи в частотной
области, с последующим преобразованием
во временную.
-
оператор обратного быстрого преобразования
Фурье. Таким образом, мы рассчитали
характеристики фильтра с заданной
передаточной характеристикой. Данный
путь расчета приводил к комплексному
коэффициенту передачи в частотной
области, с последующим преобразованием
во временную.
На
рисунках 6 и 7 показаны рассчитанные
характеристики фильтра при ![]() и
и
|
(9) |
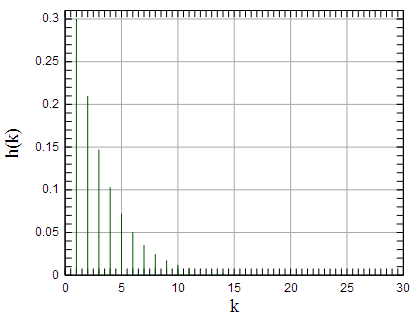
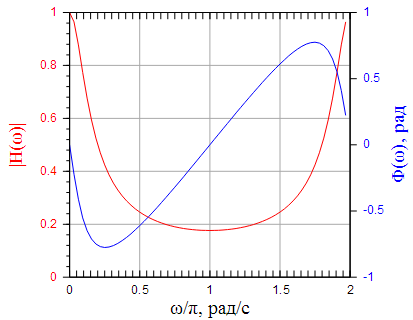
Рисунок 6: Импульсная характеристика фильтра
|
Рисунок 7: Один период АЧХ и ФЧХ фильтра
|
Обратите
внимание, что на рисунке 7 по оси абсцисс
показана частота ![]() ,
таким образом, АЧХ и ФЧХ представлена
для нормированных частот от 0 до 2. Кроме
того, можно заметить, что АЧХ
фильтра
,
таким образом, АЧХ и ФЧХ представлена
для нормированных частот от 0 до 2. Кроме
того, можно заметить, что АЧХ
фильтра ![]() является
симметричной относительно частоты
является
симметричной относительно частоты ![]() ,
или
,
или ![]() ,
т.е.
,
т.е. ![]() ,
а ФЧХ является антисимметричной, т.е.
,
а ФЧХ является антисимметричной, т.е. ![]() .
.
Рассмотрим теперь другой способ расчета характеристик фильтра — расчет во временной области. Для этого приведем структурную схему фильтра, заданного передаточной характеристикой (9) (рисунок 8).
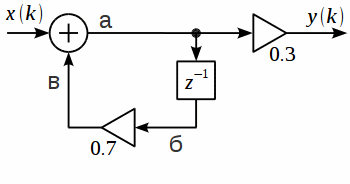 Рисунок
8: Структурная схема фильтра
Рисунок
8: Структурная схема фильтра
Для
того, чтобы получить импульсную
характеристику цифрового фильтра,
необходимо подать на вход сигнал![]() :
:
|
(10) |
Тогда на выходе фильтра будет импульсная характеристика. Рассчитаем импульсную характеристику на выходе фильтра по его структуре.
Пусть
на входе нулевой отсчет ![]() ,
тогда точка «а» равна 1, «б» и «в» равна
нулю, тогда на выходе
,
тогда точка «а» равна 1, «б» и «в» равна
нулю, тогда на выходе![]() .
При поступлении на вход отсчета
.
При поступлении на вход отсчета ![]() получим
точка «б» равна 1 (задержанная точка
«a»), точка «в» равна 0.7 и точка «а»
при
получим
точка «б» равна 1 (задержанная точка
«a»), точка «в» равна 0.7 и точка «а»
при ![]() равна
0.7, тогда
равна
0.7, тогда ![]() .
При
.
При ![]() имеем:
имеем: ![]() ,
точка «б» равна 0.7, тогда точка «в»
равна
,
точка «б» равна 0.7, тогда точка «в»
равна ![]() ,
точка «а» равна 0.49 и
,
точка «а» равна 0.49 и ![]() .
Так можно продолжать до бесконечности.
Ограничившись как и в предыдущем
случае
отсчетами
импульсной характеристики получим
полностью
совпадающую с приведенной на рисунке
выше. Тогда комплексный коэффициент
передачи фильтра можно получить если
взять БПФ от импульсной характеристики
.
.
Так можно продолжать до бесконечности.
Ограничившись как и в предыдущем
случае
отсчетами
импульсной характеристики получим
полностью
совпадающую с приведенной на рисунке
выше. Тогда комплексный коэффициент
передачи фильтра можно получить если
взять БПФ от импульсной характеристики
.
Оба приведенных способа расчета характеристик фильтра имеют приблизительно одну вычислительную сложность и какой из них выбрать решать пользователю.
Выводы
Таким образом, мы привели структурные схемы цифровых КИХ и БИХ фильтров и привели их характеристики. Была представлена структура КИХ фильтра, а также прямая и каноническая формы БИХ фильтров. Рассмотрены характеристики цифровых фильтров: комплексный коэффициент передачи, АЧХ, ФЧХ, групповая задержка и импульсная характеристика фильтра. Приведены способы численного расчета характеристик фильтра по его передаточной функции в частотной и во временной областях.
Расчет передаточной характеристики БИХ фильтра на основе аналогового фильтра прототипа. Билинейное преобразование
Содержание
Введение
Билинейное преобразование
Преобразование шкалы частот
Пояснения к отображению комплексной плоскости s в комплексную плоскость z
Выводы
Введение
В предыдущей
статье мы
рассмотрели структурные схемы, а также
характеристики цифровых фильтров при
известной передаточной функции ![]() .
Однако мы не говорили о том, как рассчитать
саму
.
В данной статье мы рассмотрим основной
на сегодняшний день метод расчета
передаточной характеристики цифрового
фильтра
на
основе передаточной характеристики
аналогового фильтра
.
Однако мы не говорили о том, как рассчитать
саму
.
В данной статье мы рассмотрим основной
на сегодняшний день метод расчета
передаточной характеристики цифрового
фильтра
на
основе передаточной характеристики
аналогового фильтра ![]() -
метод билинейного преобразования.
Мы уже
говорили о
том, что переход от передаточной
характеристики
аналогового
фильтра к
цифрового
фильтра можно осуществить переходом
-
метод билинейного преобразования.
Мы уже
говорили о
том, что переход от передаточной
характеристики
аналогового
фильтра к
цифрового
фильтра можно осуществить переходом![]() ,
где
-
период дискретизации сигнала. Но
осуществлять экспоненциальное отображение
плоскости s в плоскость z крайне не
удобно, поскольку нам бы хотелось иметь
дробно-рациональную подстановку, которую
мы умеем вычислять.
Поэтому на практике для перехода от
аналогового фильтра к цифровому
используют билинейное преобразование.
,
где
-
период дискретизации сигнала. Но
осуществлять экспоненциальное отображение
плоскости s в плоскость z крайне не
удобно, поскольку нам бы хотелось иметь
дробно-рациональную подстановку, которую
мы умеем вычислять.
Поэтому на практике для перехода от
аналогового фильтра к цифровому
используют билинейное преобразование.
Билинейное преобразование
Билинейное преобразование осуществляется подстановкой вида:
|
(1) |
Также данную подстановку можно инвертировать:
|
(2) |
Рассмотрим некоторые свойства билинейного преобразования.
Если
,
то ![]() .
.
Если ![]() -
чисто вещественно, то
-
чисто вещественно, то ![]() причем
при
причем
при ![]() модуль
модуль ![]() ,
а при
,
а при![]() модуль
модуль ![]()
Если
-
чисто мнимо, то получаем отношение
комплексно-сопряженных чисел, модуль
которого всегда равен единице, т.е. ![]() .
.
Если ![]() ,
то при
,
то при ![]() имеем
,
а при
имеем
,
а при ![]() получим
.
получим
.
Таким образом сделаем вывод. При билинейном преобразовании мнимая ось плоскости s переходит в единичную окружность на плоскости z, причем левая полуплоскость плоскости s отображается внутрь единичной окружности плоскости z, а правая полуплоскость плоскости s отображается вне единичной окружности. Отображение плоскости s в плоскость z при билинейном преобразовании показано на рисунке 1.
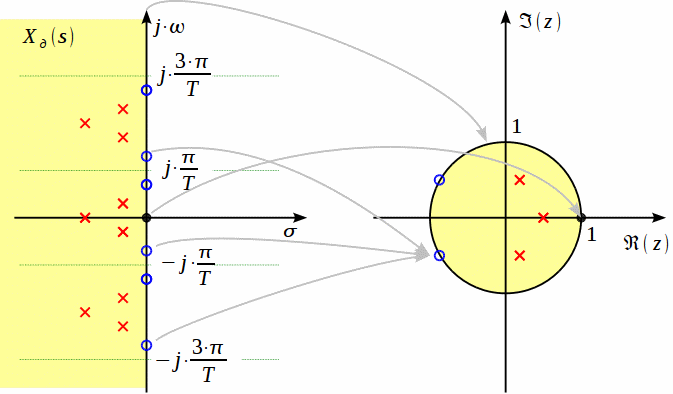 Рисунок
1: Отображение плоскости s в плоскость
z
Рисунок
1: Отображение плоскости s в плоскость
z
Данное отображение очень похоже на то, что мы приводили, когда рассматривали переход от комплексной s-плоскости в комплексную z-плоскость (подробнее здесь). Такая схожесть обуславливается тем, что выражение (2) представляет собой разложение в ряд Тейлора при ограничении степени ряда равной единицы. Действительно, разложение в ряд Тейлора экспоненты равно:
|
(3) |
Тогда можно представить:
|
(4) |
Таким образом, билинейное преобразование позволяет осуществить переход из s плоскости в z-плоскость при помощи дробно-рациональной подстановки. Поскольку в числителе и знаменателе этой подстановки полиномы только первой степени, то при переходе от передаточной характеристики аналогового фильтра к цифровому фильтру с передаточной характеристикой , максимальная степень полиномов числителя и знаменателя не изменится, а значит не измениться и порядок фильтра.
Преобразование шкалы частот
Комплексный
коэффициент передачи аналогового
фильтра
при
использовании билинейного преобразования
переходит в комплексный коэффициент
передачи дискретного фильтра![]() .
При этом мы знаем, что
-
функция периодическая, а
-
апериодическая. Обозначим как
.
При этом мы знаем, что
-
функция периодическая, а
-
апериодическая. Обозначим как ![]() циклическую
частоту аналогового фильтра, чтобы
отличить ее от циклической частоты
циклическую
частоту аналогового фильтра, чтобы
отличить ее от циклической частоты ![]() частотной
характеристики цифрового фильтра. Тогда
комплексный коэффициент передачи
аналогового фильтра обозначим как
частотной
характеристики цифрового фильтра. Тогда
комплексный коэффициент передачи
аналогового фильтра обозначим как ![]() .
Подставим теперь в выражение билинейного
преобразования (1)
.
Подставим теперь в выражение билинейного
преобразования (1)![]() и
и ![]() и
получим:
и
получим:
|
(5) |
Откуда следует, что
|
(6) |
Выражение
(6) задает частотное отображение при
билинейном преобразовании. Графически
отображение частот при билинейном
преобразовании показано на рисунке 2
при ![]() .
.
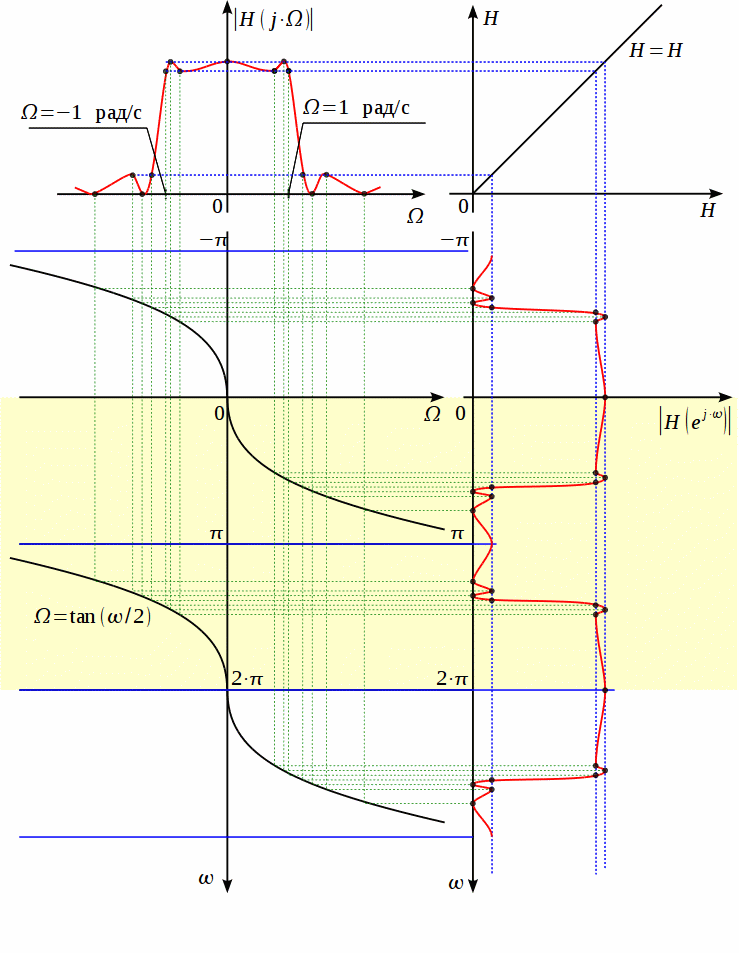 Рисунок
2: Отображение осей частот при билинейном
преобразовании
Рисунок
2: Отображение осей частот при билинейном
преобразовании
Рассмотрим
данный громоздкий рисунок 2. На верхнем
левом графике показана АЧХ ![]() аналогового
нормированного ФНЧ. На левом нижнем
графике показано частотное отображение
аналогового
нормированного ФНЧ. На левом нижнем
графике показано частотное отображение ![]() ,
соответствующее (6) при
.
Обратим внимание что тангенс - периодическая
функция, и частотная характеристика
фильтра будет многократно периодически
повторена с периодом
рад/с.
Правый верхний график показывает
проекцию АЧХ, обеспечивающий заданный
уровень боковых лепестков. И наконец,
на нижнем правом графике показана АЧХ
цифрового фильтра, полученного при
помощи билинейного преобразования из
аналогового ФНЧ. Желтым выделен один
период АЧХ цифрового фильтра.
,
соответствующее (6) при
.
Обратим внимание что тангенс - периодическая
функция, и частотная характеристика
фильтра будет многократно периодически
повторена с периодом
рад/с.
Правый верхний график показывает
проекцию АЧХ, обеспечивающий заданный
уровень боковых лепестков. И наконец,
на нижнем правом графике показана АЧХ
цифрового фильтра, полученного при
помощи билинейного преобразования из
аналогового ФНЧ. Желтым выделен один
период АЧХ цифрового фильтра.
Отметим
некоторые соотношения частот при
проекции. Нулевая частота ![]() проецируется
в частоту
.
Она же проецируется бесконечное
количество раз через
.
Частота
проецируется
в частоту
.
Она же проецируется бесконечное
количество раз через
.
Частота ![]() проецируется
на частоту
проецируется
на частоту![]() .
Таким образом, диапазон частотной
характеристики аналогового фильтра от
0 до 1 рад/с полностью размещается внутри
диапазона от 0 до
цифрового
фильтра, а частотная характеристика
от 1 до
.
Таким образом, диапазон частотной
характеристики аналогового фильтра от
0 до 1 рад/с полностью размещается внутри
диапазона от 0 до
цифрового
фильтра, а частотная характеристика
от 1 до ![]() рад/с
аналогового фильтра проецируется в
диапазон от
до
цифрового
фильтра. После через
все
повторяется.
рад/с
аналогового фильтра проецируется в
диапазон от
до
цифрового
фильтра. После через
все
повторяется.
Сделаем
еще одно важное замечание. Поскольку
функция
,
то можно сделать вывод о том что![]() ,
другими словами частотная характеристика
аналогового фильтра при
,
другими словами частотная характеристика
аналогового фильтра при ![]() из
отрицательной области частот, в силу
периодичности тангенса, переносится в
область частот
от
из
отрицательной области частот, в силу
периодичности тангенса, переносится в
область частот
от ![]() до
цифрового
фильтра. Поскольку АЧХ аналогового
фильтра с передаточной характеристикой
всегда
симметрична относительно нулевой
частоты, т.е.
до
цифрового
фильтра. Поскольку АЧХ аналогового
фильтра с передаточной характеристикой
всегда
симметрична относительно нулевой
частоты, т.е. ![]() при
вещественных коэффициентах передаточной
характеристики
,
то АЧХ цифрового фильтра, полученного
путем билинейного преобразования из
аналогового фильтра прототипа будет
симметрична относительно частоты
при
вещественных коэффициентах передаточной
характеристики
,
то АЧХ цифрового фильтра, полученного
путем билинейного преобразования из
аналогового фильтра прототипа будет
симметрична относительно частоты ![]()
Пояснения к отображению комплексной плоскости s в комплексную плоскость z
Ранее мы говорили о том, что переход из комплексной плоскости s в комплексную плоскость z существляется однозначным отображением . При этом всем нулям и полюсам фильтра в s плоскости соответствуют нули и полюса в z плоскости при фиксированном . Однако при билинейном преобразовании все нули и полюса отображаются согласно (4), при этом очевидно, что используя отображение и билинейное преобразование мы получим различные отображения одних и тех же нулей и полюсов из плоскости s в плоскость z. Именно эту разницу мы и проанализируем в данном разделе. Наиболее просто понять разницу отображения и билинейного преобразования на конкретном примере. Пусть имеется передаточная характеристика фильтра
|
(7) |
Данный
фильтр имеет единственный полюс ![]() .
Пусть интервал дискретизации
.
Найдем отображение
:
.
Пусть интервал дискретизации
.
Найдем отображение
:
|
(8) |
Отображение через билинейное преобразование дает полюс
|
(9) |
Таким образом билинейное преобразование и отображение дают различные отображения полюса из плоскости s в плоскость z, а значит мы получаем различные передаточные характеристики фильтра.
На рисунке 3 показаны АЧХ фильтров при различном отображении полюса.
 Рисунок
3: АЧХ фильтров при различном отображении
полюса
Рисунок
3: АЧХ фильтров при различном отображении
полюса
На
верхнем графике показана АЧХ ![]() полученная
при отображении полюса согласно
.
Красным показана АЧХ исходного аналогового
фильтра
полученная
при отображении полюса согласно
.
Красным показана АЧХ исходного аналогового
фильтра ![]() (деление
на
позволяет
отнормировать период дискретизации).
Синим показаны периодические повторения
АЧХ
(деление
на
позволяет
отнормировать период дискретизации).
Синим показаны периодические повторения
АЧХ ![]() ,
, ![]() .
Результирующая АЧХ
полученная
при отображении
показана
черным представляет собой сумму всех
периодических составляющих. Таким
образом, можно сделать вывод что переход
от аналогового фильтра к цифровому при
отображении
приводит
к наложению «хвостов» АЧХ аналогового
фильтра.
.
Результирующая АЧХ
полученная
при отображении
показана
черным представляет собой сумму всех
периодических составляющих. Таким
образом, можно сделать вывод что переход
от аналогового фильтра к цифровому при
отображении
приводит
к наложению «хвостов» АЧХ аналогового
фильтра.
На
втором графике показана АЧХ ![]() полученная
в результате билинейного преобразования.
Как уже было сказано выше при билинейном
преобразовании ось частот трансформируется
согласно (6), при этом все «хвосты»
аналогового фильтра укладываются в
интервал
полученная
в результате билинейного преобразования.
Как уже было сказано выше при билинейном
преобразовании ось частот трансформируется
согласно (6), при этом все «хвосты»
аналогового фильтра укладываются в
интервал ![]() ,
то есть на каждом периоде повторения
АЧХ идет «стык в стык» без наложения
«хвостов». Это принципиальное отличие
билинейного преобразования от
отображения
.
Таким образом переход от аналогового
фильтра к цифровому целесообразнее
производить через билинейное
преобразование, так как оно избавлено
от эффектов наложения в отличии от
отображения
.
,
то есть на каждом периоде повторения
АЧХ идет «стык в стык» без наложения
«хвостов». Это принципиальное отличие
билинейного преобразования от
отображения
.
Таким образом переход от аналогового
фильтра к цифровому целесообразнее
производить через билинейное
преобразование, так как оно избавлено
от эффектов наложения в отличии от
отображения
.
Выводы
Таким образом, можно сделать вывод о том, что билинейное преобразование нелинейно искажает и «периодизирует» шкалу частот, но не меняет уровня неравномерности в полосе пропускания и уровня боковых лепестков фильтра. Последнее замечание крайне важно, так как позволяет нам использовать рассчитанные передаточные характеристики аналоговых фильтров для расчета цифровых фильтров.
Рассмотренные отличия билинейного преобразования и отображения позволяют сделать вывод о том, что применение билинейного преобразования позволяет избавится от эффектов наложения при переходе от аналогового фильтра к цифровому.
Цифровые фильтры с конечной и с бесконечной импульсной характеристикой. Примеры использования в анализе финансовых рядов.
Df Физический смысл групповой задержки фильтра. Цифровые фильтры с линейной фазочастотной характеристикой
Содержание
Введение
Физический смысл ФЧХ и групповой задержки. Свойство линейности ФЧХ фильтра
Условие линейности ФЧХ фильтра
Импульсные характеристики КИХ фильтров обеспечивающие линейную ФЧХ
Выводы
Введение
Ранее мы рассмотрели структуры цифровых фильтров и их характеристики. Мы рассмотрели понятия амплитудно-частной (АЧХ), фазочастотной (ФЧХ) характеристик, а также понятие групповой задержки фильтра. В данной статье мы проанализируем физический смысл ФЧХ и групповой задержки. Рассмотрим свойство фильтров с линейной ФЧХ и получим условия линейности ФЧХ цифрового фильтра.
Физический смысл ФЧХ и групповой задержки. Свойство линейности ФЧХ фильтра
Очень часто при расчете цифровых фильтров ставится задача обеспечить постоянную групповую задержку или линейную фазочастотную характеристику (ФЧХ). В данной статье речь пойдет именно о фильтрах с линейной ФЧХ, и будут получены условия при которых цифровой фильтр будет иметь строго линейную фазочастотную характеристику.
Если
фильтр задан импульсной характеристикой ![]() ,
где
,
где ![]() ,
то его комплексный коэффициент передачи
равен:
,
то его комплексный коэффициент передачи
равен:
|
(1) |
Также вводят понятие групповой задержки как производной от ФЧХ:
|
(2) |
Смысл групповой задержки можно пояснить следующим образом. Отклик физически реализуемого фильтра всегда возникает не раньше воздействия, при этом фильтр задерживает входной сигнал при фильтрации на некоторое время. При этом если подавать на фильтр сигналы разной частоты, то сигнал на выходе одного и того же фильтра могут быть задержаны на разное время. Эта задержка выражается в сдвиге фазы сигнала на выходе относительно сигнала на входе. Групповая задержка при этом характеризует изменение временного сдвига сигнала, который получается в результате фазового сдвига. Проиллюстрируем это рисунком 1.
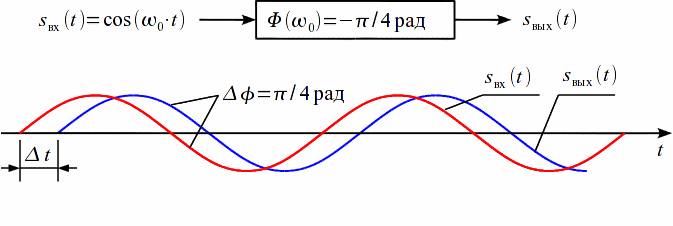 Рисунок
1: Взаимосвязь фазового и временного
сдвига сигнала
Рисунок
1: Взаимосвязь фазового и временного
сдвига сигнала
Пусть
на вход некоторого фильтра подается
сигнал ![]() ,
причем ФЧХ фильтра на частоте
сигнала
,
причем ФЧХ фильтра на частоте
сигнала ![]() равна
равна ![]() .
Тогда сигнал на выходе будет сдвинут
относительно входного на
.
Тогда сигнал на выходе будет сдвинут
относительно входного на ![]() ,
как это показано на графике. При этом
этот сдвиг фазы соответствует временному
сдвигу
,
как это показано на графике. При этом
этот сдвиг фазы соответствует временному
сдвигу ![]() .
Соответственно на некоторой другой
частоте
.
Соответственно на некоторой другой
частоте ![]() временной
сдвиг будет
временной
сдвиг будет ![]() ,
а изменение этого временного сдвига
будет зависеть от изменения ФЧХ от
частоты, т.е.
,
а изменение этого временного сдвига
будет зависеть от изменения ФЧХ от
частоты, т.е. ![]() .
Это и определяет групповая задержка:
изменение временного сдвига при изменении
частоты.
.
Это и определяет групповая задержка:
изменение временного сдвига при изменении
частоты.
Если
ФЧХ линейна, то групповая задержка ![]() постоянна,
т.е. при изменении частоты сигнала она
не меняется.
постоянна,
т.е. при изменении частоты сигнала она
не меняется.
При нелинейной ФЧХ разные частоты приобретают разные фазовые сдвиги и соответственно разные временные задержки на выходе фильтра. Чтобы понять это проведем следующий эксперимент.
Пусть имеется сигнал, у которого во времени меняется мгновенная частота. В качестве такого можно взять сигнал с фазовой модуляцией (PM) вида:
|
(3) |
П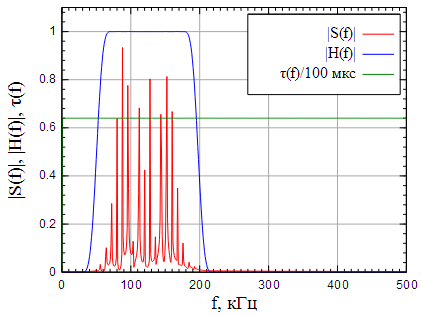
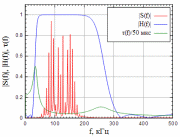 ропустим
данный сигнал через фильтр с постоянной
групповой задержкой (линейной ФЧХ) и
через фильтр с нелинейной ФЧХ, т.е.
непостоянной задержкой. Причем параметры
АЧХ
ропустим
данный сигнал через фильтр с постоянной
групповой задержкой (линейной ФЧХ) и
через фильтр с нелинейной ФЧХ, т.е.
непостоянной задержкой. Причем параметры
АЧХ ![]() фильтров
с линейной и нелинейной ФЧХ выберем
таким образом, чтобы фильтры не вносили
амплитудных искажений в амплитудный
спектр сигнала
фильтров
с линейной и нелинейной ФЧХ выберем
таким образом, чтобы фильтры не вносили
амплитудных искажений в амплитудный
спектр сигнала ![]() .
Это наглядно показано на рисунках 2 и
3. При этом на рисунках 3 и 4 показаны
осциллограммы исходного PM сигнала
(красный график) и сигналов на выходе
фильтров с линейной и нелинейной ФЧХ
(синий график) при компенсации постоянной
задержки в фильтре.
.
Это наглядно показано на рисунках 2 и
3. При этом на рисунках 3 и 4 показаны
осциллограммы исходного PM сигнала
(красный график) и сигналов на выходе
фильтров с линейной и нелинейной ФЧХ
(синий график) при компенсации постоянной
задержки в фильтре.
Рисунок 2: Фильтрация PM сигнала при помощи фильтра с линейной ФЧХ
|
Рисунок 3: Фильтрация PM сигнала при помощи фильтра с нелинейной ФЧХ
|
Рисунок 4: PM cигнал на выходе фильтра с линейной ФЧХ при компенсации задержки
|
Рисунок 5: PM cигнал на выходе фильтра с нелинейной ФЧХ при компенсации задержки
|
Из рисунка 4 следует, что сигнал на выходе фильтра полностью повторяет сигнал на входе (разумеется небольшие амплитудные искажения есть из-за неидеальности фильтра, но для нас самое главное, что фаза исходного сигнала и выходного сигнала совпадают). При этом выходной сигнал был сдвинут по оси времени для устранения постоянной задержки фильтра. Из рисунка 5 можно заметить, что скомпенсировать задержку невозможно, поскольку она меняется при изменении мгновенной частоты сигнала. Так компенсация задержки при высокой мгновенной частоте (в интервале от 100 до 150 мкс) фаза сигналов при низкой мгновенной частоте (в интервале от 50 до 100 мкс) не совпадает. Таким образом нелинейная ФЧХ фильтра привела к фазовым искажениям нашего сигнала, хотя амплитудные искажения минимальны так как АЧХ фильтра выбрана таким образом, чтобы сигнал не искажался.
Приведенный пример наглядно показывает, что нелинейная ФЧХ фильтра искажает сигнал и это надо учитывать, поскольку например при когерентной обработке искажения фазы недопустимы.
Теперь когда понятна необходимость использования фильтров с линейной ФЧХ мы исследуем свойства импульсных характеристик, которые обеспечивают эту самую линейную ФЧХ.
Условие линейности ФЧХ фильтра
Зададим линейную ФЧХ цифрового фильтра вида:
|
(4) |
где ![]() -
тангенс угла наклона ФЧХ, а
-
тангенс угла наклона ФЧХ, а ![]() .
Согласно определению, ФЧХ можно получить
из комплексного коэффициента передачи
цифрового фильтра
.
Согласно определению, ФЧХ можно получить
из комплексного коэффициента передачи
цифрового фильтра ![]() :
:
|
(5) |
Групповая
задержка фильтра при этом будет равна ![]() .
При отрицательном
мы
получим положительную групповую
задержку, что важно, так как отрицательная
задержка соответствует физически
нереализуемым фильтрам, когда отклик
на воздействие возникает раньше самого
воздействия.
.
При отрицательном
мы
получим положительную групповую
задержку, что важно, так как отрицательная
задержка соответствует физически
нереализуемым фильтрам, когда отклик
на воздействие возникает раньше самого
воздействия.
Из выражения (5) можно выразить:
|
(6) |
Откуда в свою очередь следует, что:
|
(7) |
Вспомним тригонометрические тождества, тогда (7) можно представить:
|
(8) |
После переноса в одну сторону и упрощения выражения (8) получим:
|
(9) |
Таким
образом выражение (9) задает уравнение,
которому должна удовлетворять импульсная
характеристика цифрового фильтра, чтобы
фильтр имел линейную ФЧХ. Уравнение (9)
должно выполняться при фиксированных
и ![]() и
для всех
.
и
для всех
.
Импульсные характеристики КИХ фильтров обеспечивающие линейную ФЧХ
Произведем
анализ выражения (9) для случая физически
реализуемого КИХ фильтра порядка ![]() (импульсная
характеристика содержит
(импульсная
характеристика содержит ![]() отличных
от нуля коэффициентов, а порядок фильтра
определяется количеством линий задержек
фильтра). Условие физической реализуемости
КИХ фильтра выполняется если
отличных
от нуля коэффициентов, а порядок фильтра
определяется количеством линий задержек
фильтра). Условие физической реализуемости
КИХ фильтра выполняется если ![]() при
всех
при
всех ![]() и
и ![]() .
Тогда индекс
.
Тогда индекс![]() в
сумме (9) будет принимать значения от 0
до
в
сумме (9) будет принимать значения от 0
до ![]() :
:
|
(10) |
Прежде чем вести дальнейший анализ введем понятия оси симметрии импульсной характеристики КИХ фильтра. Осью симметрии импульсной характеристики назовем значение (не обязательно целое), которое делит интервал от 0 до пополам. Чтобы понять это рассмотрим рисунок 6.
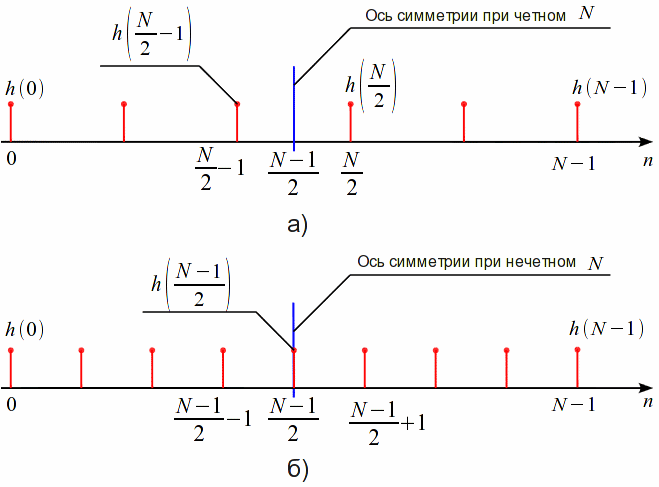 Рисунок
6: Ось симметрии имульсной характеристики
цифрового КИХ фильтра нечетного (а) и
четного (б) порядков
Рисунок
6: Ось симметрии имульсной характеристики
цифрового КИХ фильтра нечетного (а) и
четного (б) порядков
На
рисунке 6 красным условно показана
импульсная характеристика цифрового
физически реализуемого КИХ фильтра
порядка
и
отмечена ось симметрии ![]() .
Обратим внимание, что в случае нечетного
порядка
ось
симметрии
-
дробное число, а в случае четного
порядка
,
ось симметрии совпадает с «центральным
отсчетом»
.
Обратим внимание, что в случае нечетного
порядка
ось
симметрии
-
дробное число, а в случае четного
порядка
,
ось симметрии совпадает с «центральным
отсчетом» ![]() .
Напомним, что нечетный
порядок
фильтра соответствует четному
количеству
отсчетов импульсной характеристики.
.
Напомним, что нечетный
порядок
фильтра соответствует четному
количеству
отсчетов импульсной характеристики.
Рассмотрим два частных случая, при которых КИХ фильтр имеет строго линейную ФЧХ.
Фильтр
первого типа получается когда параметры
равны ![]() ,
, ![]() или
или ![]() .
Такие параметры приводят к уравнению
вида:
.
Такие параметры приводят к уравнению
вида:
|
(11) |
Уравнение
(11) выполняется если ![]() при
при ![]() ,
если
четно,
или при
,
если
четно,
или при![]() ,
если
нечетно.
Наглядно этот случай отображен на
рисунке 7.
,
если
нечетно.
Наглядно этот случай отображен на
рисунке 7.
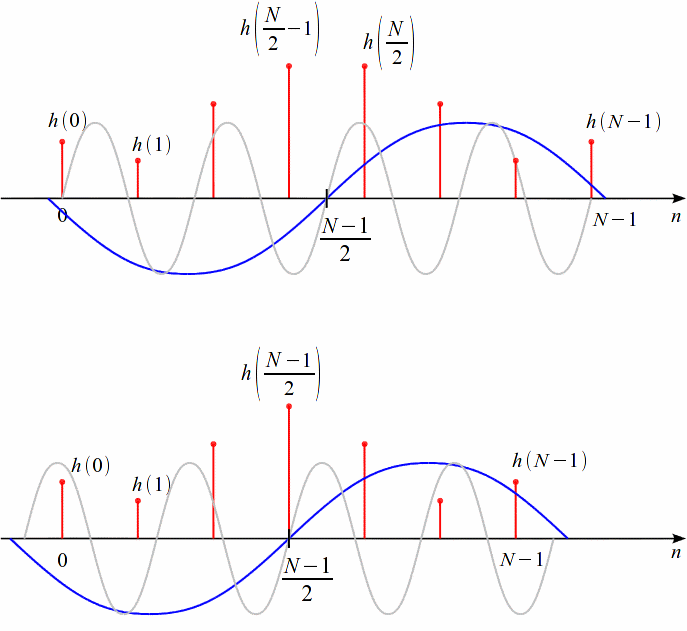 Рисунок
7: Фильтр с линейной ФЧХ и симметричной
импульсной характеристикой при нечетном
и четном порядках фильтра.
Рисунок
7: Фильтр с линейной ФЧХ и симметричной
импульсной характеристикой при нечетном
и четном порядках фильтра.
Поясним
рисунок 7. Параметр
выбран
таким образом чтобы синус ![]() всегда
имел ноль на оси симметрии, т.е. при
.
Таким образом получили синус, которые
антисимметричен относительно оси
симметрии фильтра при любой частоте
.
Тогда если справа и слева от оси симметрии
импульсная характеристика будет иметь
одинаковые значения, как это показано
на рисунке, то (11) будет иметь сумму
слагаемых с противоположными знаками,
которые взаимно скомпенсируют друг
друга и получим фильтр с линейной ФЧХ.
Важно отметить, что при четном порядке
(нижний график рисунка 7) центральный
отсчет импульсной характеристики
попадает на ноль синуса и снова получаем
фильтр с линейной ФЧХ. Таким образом
фильтр с симметричной относительно оси
симметрии импульсной характеристикой
всегда приводит к линейной ФЧХ.
всегда
имел ноль на оси симметрии, т.е. при
.
Таким образом получили синус, которые
антисимметричен относительно оси
симметрии фильтра при любой частоте
.
Тогда если справа и слева от оси симметрии
импульсная характеристика будет иметь
одинаковые значения, как это показано
на рисунке, то (11) будет иметь сумму
слагаемых с противоположными знаками,
которые взаимно скомпенсируют друг
друга и получим фильтр с линейной ФЧХ.
Важно отметить, что при четном порядке
(нижний график рисунка 7) центральный
отсчет импульсной характеристики
попадает на ноль синуса и снова получаем
фильтр с линейной ФЧХ. Таким образом
фильтр с симметричной относительно оси
симметрии импульсной характеристикой
всегда приводит к линейной ФЧХ.
Параметры
для фильтр второго типа следующие:
, ![]() или
или ![]() .
Тогда получаем уравнение вида:
.
Тогда получаем уравнение вида:
|
(12) |
Уравнение
(12) выполняется если ![]() при
,
если
четно,
или при
,
если
нечетно.
Наглядно этот случай отображен на
рисунке 8.
при
,
если
четно,
или при
,
если
нечетно.
Наглядно этот случай отображен на
рисунке 8.
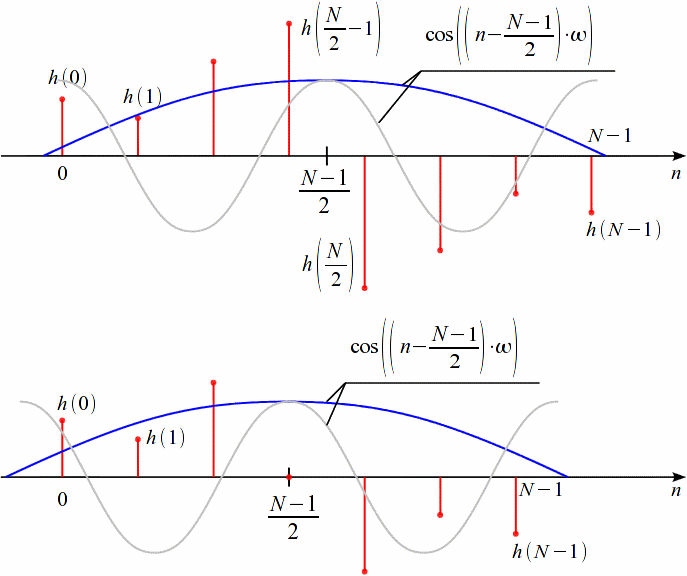 Рисунок
8: Фильтр с линейной ФЧХ и антисимметричной
импульсной характеристикой
Рисунок
8: Фильтр с линейной ФЧХ и антисимметричной
импульсной характеристикой
Поясним
рисунок 8. Параметр
выбран
таким образом чтобы ![]() всегда
имел единицу на оси симметрии, т.е. при
.
Таким образом получили косинус, который
симметричен относительно оси симметрии
фильтра при любой частоте
.
Тогда если справа и слева от оси симметрии
импульсная характеристика будет иметь
противоположные значения, как это
показано на рисунке, то (12) будет иметь
сумму слагаемых с противоположными
знаками, которые взаимно скомпенсируют
друг друга и получим фильтр с линейной
ФЧХ. Важно отметить что при четном
порядке (нижний график рисунка 8)
центральный отсчет импульсной
характеристики попадает на единицу и
он должен быть нулевым для фильтра с
линейной ФЧХ. Таким образом фильтр с
антисимметричной относительно оси
симметрии импульсной характеристикой
всегда приводит к линейной ФЧХ.
всегда
имел единицу на оси симметрии, т.е. при
.
Таким образом получили косинус, который
симметричен относительно оси симметрии
фильтра при любой частоте
.
Тогда если справа и слева от оси симметрии
импульсная характеристика будет иметь
противоположные значения, как это
показано на рисунке, то (12) будет иметь
сумму слагаемых с противоположными
знаками, которые взаимно скомпенсируют
друг друга и получим фильтр с линейной
ФЧХ. Важно отметить что при четном
порядке (нижний график рисунка 8)
центральный отсчет импульсной
характеристики попадает на единицу и
он должен быть нулевым для фильтра с
линейной ФЧХ. Таким образом фильтр с
антисимметричной относительно оси
симметрии импульсной характеристикой
всегда приводит к линейной ФЧХ.
Теперь необходимо сделать замечания.
Замечание 1. КИХ фильтры с симметричной или антисимметричной импульсной характеристикой лишь частный случай КИХ фильтров с линейной ФЧХ. Возможно обеспечить линейную ФЧХ КИХ фильтра при нарушении симметрии импульсной характеристики, но для большинства задач это не является необходимым.
Замечание 2. Поскольку БИХ фильтры не обладают свойствами симметрии импульсной характеристики и не могут иметь линейную ФЧХ. В книге [ОШ2 стр. 307] упоминается , что существует доказательство невозможности построения физически реализуемого БИХ фильтра с линейной ФЧХ.
Выводы
В данной статье мы проанализировали физический смысл ФЧХ и групповой задержки. Было установлено, что групповая задержка показывает изменение задержки сигнала на выходе фильтра при изменении частоты сигнала на входе. При этом нелинейная ФЧХ фильтра может исказить сигнал с изменяющейся во времени мгновенной частотой и это надо учитывать при когерентной обработке. Также были сформулированы требования к импульсной характеристике цифрового фильтра и получены условия при которых КИХ фильтр обладает строго линейной ФЧХ. Показано, что КИХ фильтры с импульсной характеристикой симметричной (антисимметричной) относительно оси симметрии обладают линейной ФЧХ. Полученные условия будут использованы при проектировании цифровых КИХ фильтров.
Расчет КИХ фильтра с линейной фазочастотной характеристикой методом частотной выборки
Содержание
Введение
Расчет КИХ фильтра с произвольной АЧХ и линейной ФЧХ методом частотной выборки
Численный расчет КИХ фильтра на основе обратного дискретного преобразования Фурье (ОДПФ)
Эффект Гиббса при расчете фильтров методом частотной выборки
Выводы
Введение
В предыдущей статье мы подробно рассмотрели физический смысл такой характеристики цифрового фильтра, как групповая задержка. Было показано, что БИХ фильтры с нелинейной фазочастотной характеристикой (ФЧХ) вносят в сигнал фазовые искажения, что часто бывает недопустимо если информация передается при помощи фазовой модуляции. Поэтому особое внимание уделяется фильтром с линейной ФЧХ и постоянной групповой задержкой, которые все частоты задерживают на одну и туже постоянную величину, которая может быть учтена при обработке.
Мы также выяснили, что линейная ФЧХ достижима только в случае конечной импульсной характеристики фильтра, причем существует 4 вида импульсных характеристик, которые обеспечивают линейную ФЧХ.
В данной статье мы рассмотрим порядок расчета КИХ фильтра по произвольно заданной амплитудно-частотной характеристике (АЧХ) с линейной ФЧХ методом частотной выборки.
Предварительно сделаем несколько замечаний, которые обсуждались ранее, но необходимо их вспомнить для понимания текущего материала.
Замечание
1. Необходимо вспомнить, что для КИХ
фильтров ![]() –
количество коэффициентов импульсной
характеристики
–
количество коэффициентов импульсной
характеристики![]() на
единицу больше чем порядок фильтра
на
единицу больше чем порядок фильтра ![]() .
Напомним, что порядок фильтра всегда
равен количеству линий задержки
структурной схемы КИХ фильтра, показанной
на рисунке 1 (подробно о структурных
схемах цифровых фильтров можно
почитать здесь).
.
Напомним, что порядок фильтра всегда
равен количеству линий задержки
структурной схемы КИХ фильтра, показанной
на рисунке 1 (подробно о структурных
схемах цифровых фильтров можно
почитать здесь).
 Рисунок
1: структурная схема КИХ фильтра
Рисунок
1: структурная схема КИХ фильтра
Замечание 2. Коэффициенты КИХ фильтра равны значениям отсчетов импульсной характеристики . Таким образом фильтры четного порядка содержат нечетное количество коэффициентов, а фильтры нечетного порядка — четное.
Замечание
3. ФЧХ цифрового фильтра ![]() связана
с групповой задержкой
связана
с групповой задержкой ![]() как
как
|
(1) |
откуда
|
(2) |
Замечание 4. Обозначим 4 типа импульсных характеристик КИХ фильтра, обладающих линейной ФЧХ как это показано на рисунке 2. Подробно все эти типы были рассмотрены в предыдущей статье.
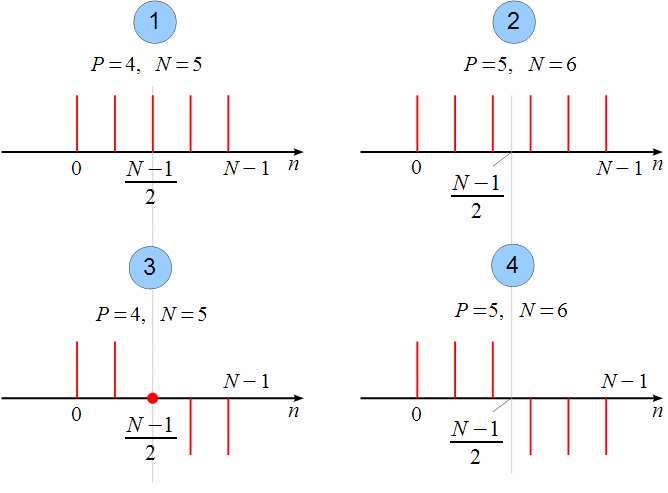 Рисунок
2: Типы импульсных характеристик КИХ
фильтров с линейной ФЧХ
Рисунок
2: Типы импульсных характеристик КИХ
фильтров с линейной ФЧХ
Фильтр
1-го типа. Фильтр четного порядка ![]() с
нечетным количеством коэффициентов
с
нечетным количеством коэффициентов ![]() .
Импульсная характеристика симметрична
относительно отсчета
.
Импульсная характеристика симметрична
относительно отсчета ![]() ,
т. е.
,
т. е. ![]() ,
при этом ось симметрии попадает на
данный отсчет.
,
при этом ось симметрии попадает на
данный отсчет.
Фильтр
2-го типа. Фильтр нечетного порядка
с
четным количеством коэффициентов
.
Импульсная характеристика симметрична
относительно оси симметрии ![]() ,
т. е.
.
,
т. е.
.
Фильтр
3-го типа. Фильтр четного порядка
с
нечетным количеством коэффициентов
.
Импульсная характеристика антисимметрична
относительно отсчета
,
т. е. ![]() при
этом ось симметрии попадает на центральный
отсчет, который должен быть равен нулю
при
этом ось симметрии попадает на центральный
отсчет, который должен быть равен нулю ![]() .
.
Фильтр 4-го типа. Фильтр нечетного порядка с четным количеством коэффициентов . Импульсная характеристика антисимметрична относительно оси симметрии , т. е. .
Обратим внимание, что фильтры четного и нечетного порядков вносят задержку при фильтрации, совпадающую с осью симметрии и равную . Таким образом, групповая задержка КИХ фильтра с линейной ФЧХ должна быть постоянной и равна .
Расчет КИХ фильтра с произвольной АЧХ и линейной ФЧХ методом частотной выборки
Пусть
задана АЧХ КИХ фильтра ![]() аналитически,
или предварительно измеренная каким-либо
способом. АЧХ
КИХ
фильтра — периодическая, четная функция
с периодом
аналитически,
или предварительно измеренная каким-либо
способом. АЧХ
КИХ
фильтра — периодическая, четная функция
с периодом ![]() рад/c,
как это показано на рисунке 3.
рад/c,
как это показано на рисунке 3.
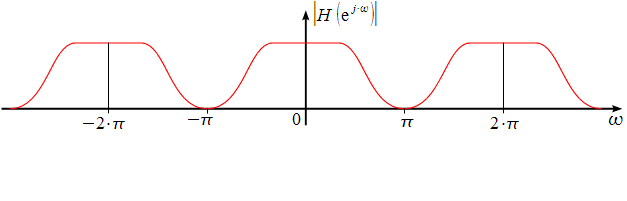 Рисунок
3: Периодическая симметричная АЧХ КИХ
фильтра
Рисунок
3: Периодическая симметричная АЧХ КИХ
фильтра
Важно
вспомнить, что частота цифрового фильтра
всегда нормирована к частоте дискретизации,
поэтому все частотные характеристики
фильтров задаются на интервале от 0
до ![]() рад/c.
рад/c.
Если
бы у нас был комплексный коэффициент
передачи фильтра ![]() (без
модуля), то мы могли бы произвести расчет
импульсной характеристики как разложение
в ряд Фурье периодической функции
:
(без
модуля), то мы могли бы произвести расчет
импульсной характеристики как разложение
в ряд Фурье периодической функции
:
|
(3) |
Но
у нас задана только АЧХ, т.е. модуль
комплексного коэффициента передачи
,
поэтому мы должны добавить ФЧХ ![]() ,
тогда:
,
тогда:
|
(4) |
и можно использовать выражение (3).
Таким
образом, мы должны к требуемой АЧХ задать
линейную ФЧХ и рассчитать КИХ согласно
(3). Для того чтобы правильно задать
линейную ФЧХ мы должны потребовать,
чтобы фильтр вносил постоянную групповую
задержку![]() для
любого из четырех типов фильтров. Тогда
согласно (2)
для
любого из четырех типов фильтров. Тогда
согласно (2)
|
(5) |
При расчете неопределенного интеграла постоянная интегрирования приравнена к нулю.
Окончательно выражение для импульсной характеристики КИХ фильтра с линейной ФЧХ принимает вид:
|
(6) |
Данное выражение позволяет произвести аналитический расчет импульсной характеристики КИХ фильтра с линейной ФЧХ, что очень важно. Однако, на практике АЧХ может не быть задана аналитически, а даже если и задана, то аналитическое интегрирование не всегда возможно. Поэтому нам бы хотелось производить численный расчет импульсной характеристики КИХ фильтра с произвольной АЧХ, чем мы и займемся дальше.
Численный расчет КИХ фильтра на основе обратного дискретного преобразования Фурье (ОДПФ)
Мы уже говорили о том, что требуется алгоритм численного расчета (6), ввиду сложностей с аналитическим вычислением интеграла (6). Для этой цели мы можем продискретизировать комплексный коэффициент передачи КИХ фильтра как это показано на рисунке 4 и рисунке 5 для четного и нечетного количества коэффициентов КИХ фильтра соответственно. К такому приему мы уже прибегали при переходе от интеграла Фурье к дискретному преобразованию.
 Рисунок
4: Дискретизация периодической АЧХ и
ФЧХ КИХ фильтра при четном N
Рисунок
4: Дискретизация периодической АЧХ и
ФЧХ КИХ фильтра при четном N
 Рисунок
5: Дискретизация периодической АЧХ и
ФЧХ КИХ фильтра при нечетном N
Рисунок
5: Дискретизация периодической АЧХ и
ФЧХ КИХ фильтра при нечетном N
Дискретизацию будем осуществлять на равноотстоящей сетке:
|
(7) |
Тогда АЧХ и ФЧХ дискретизируются на данной сетке частот и комплексный коэффициент передачи представляется дискретными отсчетами:
|
(8) |
где ![]() –
дельта-функция:
–
дельта-функция:
|
(9) |
Подставив выражение (8) в (6) получим:
|
(10) |
В выражении (10) операции интегрирования и суммирования поменяны местами и применено фильтрующее свойство дельта-функции.
Учтем (7) и окончательно можно записать:
|
(11) |
Выражение (11) ничто иное, как обратное дискретное преобразование Фурье (ОДПФ) комплексного коэффициента передачи
|
(12) |
Это позволяет производить численный расчет КИХ фильтра с произвольной АЧХ с применением алгоритмов быстрого преобразования Фурье, что существенно увеличивает эффективность данного метода.
Сделаем очень важное замечание. При расчете необходимо правильно дискретизировать ФЧХ комплексного коэффициента передачи, так как это показано на рисунках 3 и 5. Так для фильтра с четным количеством коэффициентов ФЧХ дискретизируется согласно выражению (смотри рисунок 3):
|
(13) |
В случае нечетного количества коэффициентов КИХ фильтра , ФЧХ дискретизируется согласно выражению (смотри рисунок 5):
|
(14) |
В случае четного мы получим КИХ фильтр 2-го или 4-го типа, а при нечетном – первого или третьего типа.
Такая дискретизация ФЧХ необходима, чтобы обеспечить свойства симметрии комплексного коэффициента передачи фильтра, который по сути – дискретное преобразование Фурье от импульсной характеристики КИХ фильтра. Поскольку импульсная характеристика должна быть чисто вещественной, то необходимо выдерживать симметрию АЧХ и ФЧХ, иначе при расчете импульсной характеристики при помощи ОДПФ появится мнимая часть.
Эффект Гиббса при расчете фильтров методом частотной выборки
Основное
достоинство метода частотной выборки
заключается в том, что он позволяет
довольно просто рассчитать КИХ фильтр
с линейной ФЧХ и произвольной АЧХ,
заданной на сетке частот ![]() .
Для этого требуется построить комплексный
коэффициент передачи фильтра
.
Для этого требуется построить комплексный
коэффициент передачи фильтра ![]() на
заданной сетке частот, и взять от него
обратное дискретное преобразование
Фурье. Однако при всей простоте данного
метода, он хранит в себе подводные камни.
Рассмотрим на примере.
на
заданной сетке частот, и взять от него
обратное дискретное преобразование
Фурье. Однако при всей простоте данного
метода, он хранит в себе подводные камни.
Рассмотрим на примере.
Пусть ![]() и
нам требуется рассчитать ФНЧ с частотой
среза
и
нам требуется рассчитать ФНЧ с частотой
среза ![]() .
Аналитически заданная АЧХ ФНЧ, и ее
дискретные отсчеты показаны на рисунке
6.
.
Аналитически заданная АЧХ ФНЧ, и ее
дискретные отсчеты показаны на рисунке
6.
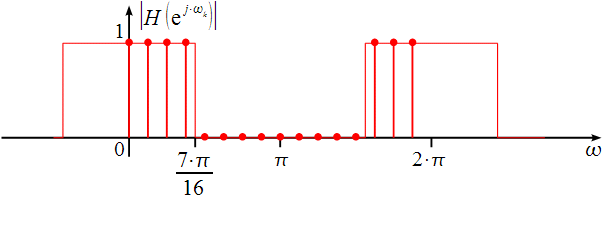 Рисунок
6: Дискретизация периодической АЧХ ФНЧ
при N = 16
Рисунок
6: Дискретизация периодической АЧХ ФНЧ
при N = 16
На рисунке 7 показаны отсчеты линейной ФЧХ, взятые в соответствии с выражением (13) при четном .
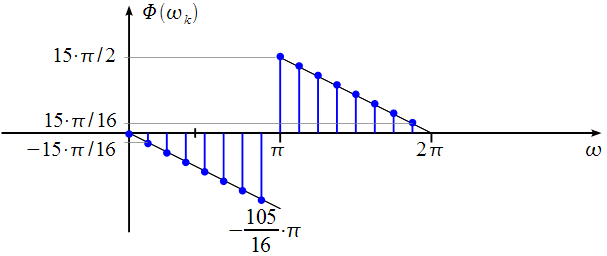 Рисунок
7: Дискретизация линейной ФЧХ ФНЧ при N
= 16
Рисунок
7: Дискретизация линейной ФЧХ ФНЧ при N
= 16
Таким образом, мы можем сформировать отсчеты комплексного коэффициента передачи как:
|
(15) |
Значения реальной и мнимой частей комплексного коэффициента передачи (15) приведены в таблице:
|
|
|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
+1.0000000 -0.9807853 +0.9238795 -0.8314696 +0.0000000 -0.0000000 +0.0000000 -0.0000000 -0.0000000 -0.0000000 +0.0000000 -0.0000000 +0.0000000 -0.8314696 +0.9238795 -0.9807853 |
-0.0000000 -0.1950903 +0.3826834 -0.5555702 +0.0000000 -0.0000000 +0.0000000 -0.0000000 -0.0000000 +0.0000000 -0.0000000 +0.0000000 -0.0000000 +0.5555702 -0.3826834 +0.1950903 |
Для расчета коэффициентов фильтра необходимо взять ОДПФ от комплексного коэффициента передачи (15):
|
(16) |
В
нашем случае
кратно
степени двойки, и можно воспользоваться
алгоритмом быстрого преобразования
Фурье. Результат расчета импульсной
характеристики ![]() КИХ
фильтра с линейной ФЧХ приведен в
таблице:
КИХ
фильтра с линейной ФЧХ приведен в
таблице:
|
|
|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
-0.0485469 +0.0307880 +0.0678165 -0.0079250 -0.0980449 -0.0384873 +0.1898828 +0.4045168 +0.4045168 +0.1898828 -0.0384873 -0.0980449 -0.0079250 +0.0678165 +0.0307880 -0.0485469 |
-0.0000000 -0.0000000 -0.0000000 -0.0000000 +0.0000000 +0.0000000 -0.0000000 -0.0000000 -0.0000000 -0.0000000 +0.0000000 +0.0000000 -0.0000000 +0.0000000 +0.0000000 +0.0000000 |
Нельзя
забывать, что в общем случае результат
при обратном дискретном преобразовании
Фурье является комплексным, поэтому в
таблице приведена как реальная
,
так и мнимая
части
импульсной характеристики
.
Однако, поскольку мы воспользовались
свойствами симметрии дискретного
преобразования Фурье при дискретизации
комплексного коэффициента передачи
фильтра, в частности его линейной ФЧХ,
то мнимая часть в нашем случае равна
нулю (на практике она отличается от нуля
ввиду ошибок округления при расчете,
но имеет очень маленькие значения ![]() и
меньше) и импульсная характеристика
чисто
вещественная.
и
меньше) и импульсная характеристика
чисто
вещественная.
Замечание. Если при расчете вы получили мнимую часть отличную от нуля, то это означает, что при дискретизации комплексного коэффициента передачи допущена ошибка.
На рисунке 7 показан вид импульсной характеристики рассчитанного фильтра. Как можно заметить, получен фильтр 2-го типа с симметричной импульсной характеристикой и линейной ФЧХ.
|
|
На рисунке 8 показана АЧХ рассчитанного фильтра (красный график), которая, как видно, точно проходит через узлы дискретизации, однако между точками дискретизации сильно отличается от идеальной характеристики. При этом наблюдается сильная неравномерность АЧХ в полосе пропускания фильтра, и высокий уровень боковых лепестков в полосе заграждения.
Данный эффект носит название эффекта Гиббса и возникает ввиду ограничения количества отсчетов импульсной характеристики.
Физический смысл эффекта Гиббса заключается в следующем: при дискретизации АЧХ мы задаем точки через которые должна пройти АЧХ рассчитанного фильтра, однако мы не накладываем никаких ограничений на поведение АЧХ в других точках. При расчете мы получаем набор коэффициентов КИХ фильтра как разложение в ряд Фурье комплексного коэффициента передачи. Эти коэффициенты разложение мы рассчитываем через обратное дискретное преобразование Фурье. Поскольку мы ограничиваем количество коэффициентов разложения (количество коэффициентов КИХ фильтра), то получаем усеченный ряд, который лишь аппроксимирует идеальную АЧХ. Аппроксимация будет тем лучше, чем больше коэффициентов импульсной характеристики, т. е. чем чаще мы будем дискретизировать идеальную АЧХ. Эффект Гиббса – негативный эффект, который не позволяет получить КИХ фильтр высокой избирательности. Поэтому было предложено использовать для расчета КИХ фильтров аппарат весовых окон, которые были рассмотрены при спектральном анализе ограниченных во времени сигналов. Использование весовых окно позволяет улучшить частотные характеристики КИХ фильтров, о чем пойдет речь в следующей статье.
Выводы
В данной статье мы рассмотрели алгоритм расчета коэффициентов КИХ фильтра произвольной АЧХ и линейной ФЧХ на основе частотной выборки. Мы показали что численный расчет импульсной характеристики фильтра производится на основе обратного дискретного преобразования Фурье после дискретизации комплексного коэффициента передачи, при этом возможно использование эффективных алгоритмов быстрого преобразования Фурье. Приведен пример расчета КИХ фильтра и показано, что при ограничении порядка фильтра возникает эффект Гиббса – негативный эффект, который искажает АЧХ фильтра, снижая избирательный свойства.
Расчет КИХ фильтра с линейной фазочастотной характеристикой методом частотной выборки с применением оконного сглаживания
Содержание
Введение
Уменьшение эффекта Гиббса при использовании оконного сглаживания
Практические рекомендации по выбору оконной функции при расчете КИХ фильтров
Выводы
Введение
В
предыдущей статье мы рассмотрели расчет
КИХ фильтра с линейной ФЧХ методом
частотной выборки на
основе обратного дискретного преобразования
Фурье от дискретизированного в частотной
области комплексного коэффициента
передачи![]() .
При этом мы показали, что использование
метода частотной выборки приводит к
финитной импульсной характеристике
фильтра
.
При этом мы показали, что использование
метода частотной выборки приводит к
финитной импульсной характеристике
фильтра ![]() ,
–
количество коэффициентов КИХ фильтра,
что в свою очередь сопровождается
эффектом Гиббса. Эффект Гиббса заключается
в том, что АЧХ полученного фильтра
полностью совпадает с требуемой АЧХ в
узлах частотной выборки, т.е. в узлах
дискретизации комплексного коэффициента
передачи
,
но отличается от требуемой АЧХ между
узлами частотной выборки, как это
показано на рисунке 1 для КИХ фильтра
при
.
,
–
количество коэффициентов КИХ фильтра,
что в свою очередь сопровождается
эффектом Гиббса. Эффект Гиббса заключается
в том, что АЧХ полученного фильтра
полностью совпадает с требуемой АЧХ в
узлах частотной выборки, т.е. в узлах
дискретизации комплексного коэффициента
передачи
,
но отличается от требуемой АЧХ между
узлами частотной выборки, как это
показано на рисунке 1 для КИХ фильтра
при
.
 Рисунок
1: Эффект Гиббса при расчете КИХ фильтра
Рисунок
1: Эффект Гиббса при расчете КИХ фильтра
Видно, что АЧХ идеального ФНЧ, комплексный коэффициент передачи которого был дискретизирован, перестает быть идеальным и приобретает неравномерность в полосе пропускания и боковые лепестки в полосе заграждения ввиду ограничения количества коэффициентов фильтра.
Примечательным
свойством эффекта Гиббса является тот
факт, что уровень приобретаемой
неравномерности в полосе пропускания
и уровень боковых лепестков в полосе
заграждения не уменьшается с ростом
количества коэффициентов фильтра, что
наглядно показано на рисунке 2 для
АЧХ ![]() ФНЧ
при различном количестве коэффициентов
фильтра
от
16 до 128.
ФНЧ
при различном количестве коэффициентов
фильтра
от
16 до 128.
|
|
|
|
Рисунок 2: Уровень неравномерности в полосе пропускания и боковых лепестков в полосе заграждения при увеличении количества коэффициентов КИХ фильтра
Из рисунка 2 можно заметить, что с увеличением количества коэффициентов КИХ фильтра возрастает количество боковых лепестков, но максимальный уровень первого бокового лепестка практически не уменьшается, как не уменьшается и максимальная неравномерность АЧХ в полосе пропускания. Также можно заметить, что с ростом неравномерность в полосе пропускания возрастает ближе к частоте среза фильтра, а скорость спада боковых лепестков растет.
Напомним, что количество коэффициентов КИХ фильтра на единицу больше порядка фильтра . Порядок фильтра равен количеству линий задержки, необходимое для реализации данного фильтра.
В данной статье мы рассмотрим расчет КИХ фильтров с линейной ФЧХ методом частотной выборки с применением оконного сглаживания (в англоязычной литературе window method), который позволяет регулировать уровень боковых лепестков АЧХ в полосе заграждения, и неравномерность АЧХ в полосе пропускания.
Уменьшение эффекта Гиббса при использовании оконного сглаживания
Простота и высокая вычислительная эффективность метода частотной выборки делает его очень привлекательным для практического использования, однако на выходе получается фильтр с очень высоким уровнем боковых лепестков в полосе заграждения и неравномерностью в полосе пропускания, что привело к необходимости доработки метода частотной выборки для практического применения.
Отметим, что такие боковые лепестки возникают ввиду резкого перехода от частоты пропускания к частоте подавления и возникают из-за интерполяции дискретизированного комплексного коэффициента передачи фильтра. Для того, чтобы уменьшить уровень боковых лепестков, необходимо сгладить переход между полосой пропускания и заграждения как это показано на рисунке 3.
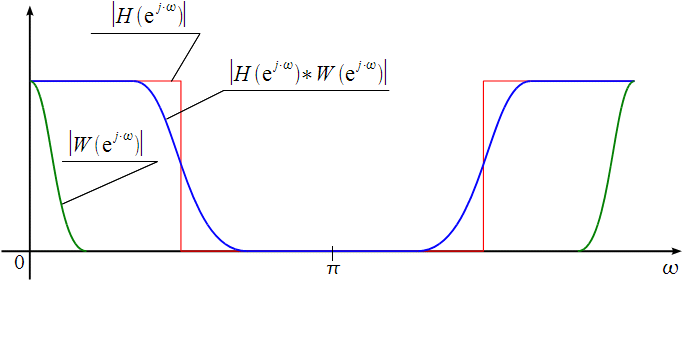 Рисунок
3: Сглаживание перехода между полосой
пропускания и заграждения
Рисунок
3: Сглаживание перехода между полосой
пропускания и заграждения
Исходный
комплексный коэффициент передачи
идеального фильтра
(красная
АЧХ) сворачивается с комплексным
коэффициентом передачи ![]() (зеленая
АЧХ) и получается сглаженная АЧХ (синяя),
у которой нет резкого перехода. Мы
искусственно вводим еще один комплексный
коэффициент передачи
,
который можем менять, и у нас появляется
возможность регулировки уровня боковых
лепестков нашего фильтра, рассчитанного
на основе частотной выборки. Очевидно,
что идеальная АЧХ при сглаживании
искажается и появляется переходная
полоса между полосой пропускания и
заграждения, но это искажение мы можем
регулировать при помощи
,
в отличии от искажений возникающих в
результате эффекта Гиббса. Функцию
можно
считать спектральным окном, а
свертку
(зеленая
АЧХ) и получается сглаженная АЧХ (синяя),
у которой нет резкого перехода. Мы
искусственно вводим еще один комплексный
коэффициент передачи
,
который можем менять, и у нас появляется
возможность регулировки уровня боковых
лепестков нашего фильтра, рассчитанного
на основе частотной выборки. Очевидно,
что идеальная АЧХ при сглаживании
искажается и появляется переходная
полоса между полосой пропускания и
заграждения, но это искажение мы можем
регулировать при помощи
,
в отличии от искажений возникающих в
результате эффекта Гиббса. Функцию
можно
считать спектральным окном, а
свертку ![]() называют
оконным сглаживанием.
называют
оконным сглаживанием.
Мы
уже однажды прибегали к оконному
сглаживанию, когда рассматривали спектральный
анализ ограниченных во времени сигналов.
По сути в данном случае имеем дело с тем
же самым анализом ограниченного во
времени сигнала, в качестве импульсной
характеристики КИХ фильтра
,
чей спектр представляет собой АЧХ КИХ
фильтра.
Свертка
комплексного коэффициента и спектрального
окна в частотной области, при переходе
во временную область, согласносвойствам
преобразования Фурье,
соответствует произведению импульсной
характеристики
и
оконной функции ![]() ,
,![]() .
При этом ранее мы рассматривали множество
различных оконных функций, позволяющих
обеспечить различное подавление боковых
лепестков и различное расширение
переходной полосы. Посмотреть вид
различных оконных функций можно вэтом
приложении.
.
При этом ранее мы рассматривали множество
различных оконных функций, позволяющих
обеспечить различное подавление боковых
лепестков и различное расширение
переходной полосы. Посмотреть вид
различных оконных функций можно вэтом
приложении.
Сделаем очень важное замечание. Все рассмотренные ранее оконные функции являются симметричными, т.е.
|
(1) |
Это означает что импульсная характеристика
|
(2) |
также будет соответствовать фильтру с линейной ФЧХ, поскольку свойства симметрии и антисимметрии, необходимые для обеспечения линейной ФЧХ не нарушатся (подробнее об этом мы говорили в этой статье).
На рисунке 4 показаны АЧХ фильтра нижних частот рассчитанного методом частотной выборки без оконного сглаживания (красный график) и с окном Хэмминга (синий) и Блэкмана (черный).
|
|
Рисунок 4: АЧХ КИХ фильтра при использовании оконного сглаживания
Из
рисунка 4 отчетливо видно, что применение
оконных функций обеспечивает снижение
уровня боковых лепестков, уменьшает
неравномерность в полосе пропускания,
но также приводит к расширению переходной
полосы. Важно отметить, что точкой
пересечения АЧХ при использовании
оконного сглаживания и без него является
точка по уровню ![]() .
.
Практические рекомендации по выбору оконной функции при расчете КИХ фильтров
БИХ фильтры мы рассчитывали на основе задания требуемых характеристик в виде коридора АЧХ (смотри здесь). Аналогично можно задать коридор АЧХ для КИХ ФНЧ как это показано на рисунке 5.
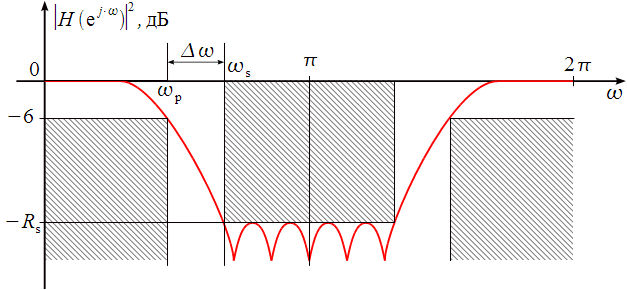 Рисунок
5: Коридор АЧХ для расчета КИХ фильтра
методом частотной выборки с оконным
сглаживанием
Рисунок
5: Коридор АЧХ для расчета КИХ фильтра
методом частотной выборки с оконным
сглаживанием
Необходимо
выбрать количество коэффициентов КИХ
фильтра для обеспечения заданной
переходной полосы ![]() и
оконную функцию для обеспечения заданного
подавления в полосе заграждения
и
оконную функцию для обеспечения заданного
подавления в полосе заграждения ![]() .
.
Первый
шаг – выбор оконной функции для
обеспечения заданного подавления в
полосе заграждения. У оконной функции
есть параметр ![]() задающий
уровень боковых лепестков спектрального
окна. Необходимо выбрать оконную функцию
у которой
задающий
уровень боковых лепестков спектрального
окна. Необходимо выбрать оконную функцию
у которой
|
(3) |
Теперь надо рассчитать требуемое количество коэффициентов импульсной характеристики фильтра по формуле
|
(4) |
где ![]() –
параметр оконной функции, задающий
расширение переходный полосы (приведен
в таблице 2 в
приложении).
–
параметр оконной функции, задающий
расширение переходный полосы (приведен
в таблице 2 в
приложении).
Приведем
пример. Пусть требуется рассчитать КИХ
ФНЧ со следующими параметрами: ![]() ,
, ![]() ,
,![]() .
.
Шаг
первый выбираем оконную функцию у
которой ![]() .
Из таблицы
2 можно
выбрать окно Хемминга с
.
Из таблицы
2 можно
выбрать окно Хемминга с![]() и
коэффициентом расширения
и
коэффициентом расширения ![]() ,
тогда
,
тогда
|
(5) |
На
рисунке 6 показан вид импульсной
характеристики КИХ фильтра при ![]() и
сглаживающем окне Хемминга, а также его
АЧХ
и
сглаживающем окне Хемминга, а также его
АЧХ
|
|
Рисунок 6: Импульсная характеристика и АЧХ рассчитанного фильтра
Видно, что АЧХ полученного фильтра удовлетворяет требуемому коридору.
Выводы
В данной статье мы рассмотрели расчет цифровых КИХ фильтром методом частотной выборки с применением оконного сглаживания для уменьшения эффекта Гиббса и улучшения характеристик фильтра. Приведены практические рекомендации по выбору оконной функции и количества коэффициентов КИХ фильтра для расчета по заданному коридору АЧХ фильтра. Многообразие оконных функций позволяет рассчитать КИХ фильтр под любые практические задачи, однако ученые на этом не успокоились. Кайзером было предложено параметрическое окно, обеспечивающее квазиоптиоптимальные характеристики фильтра, рассчитанного методом частотной выборки с оконным сглаживанием. Кроме того был разработан метод оптимальной Чебышевской аппроксимации комплексного коэффициента передачи КИХ фильтра с линейной ФЧХ, который мы рассмотрим в следующих разделах.
Адаптивные фильтры. Фильтр Калмана.





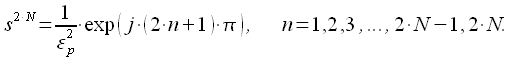
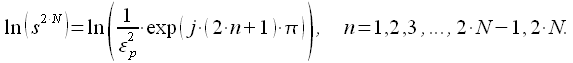


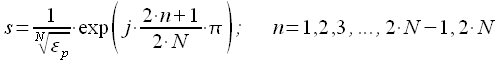
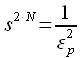
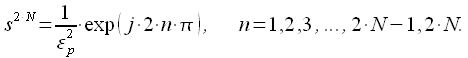
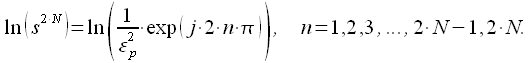
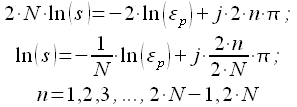

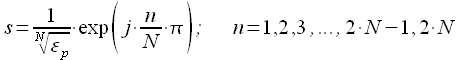
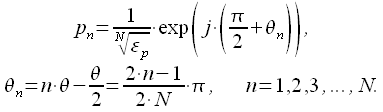
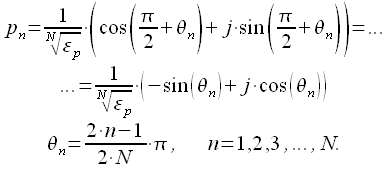
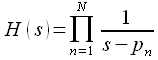

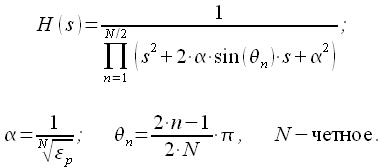
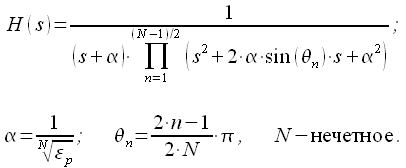

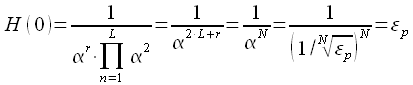
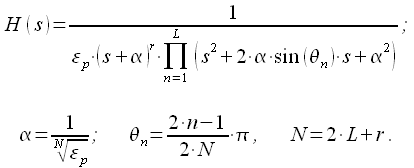
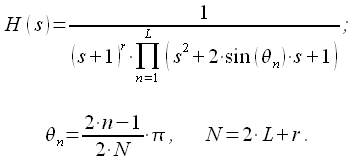
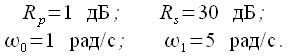
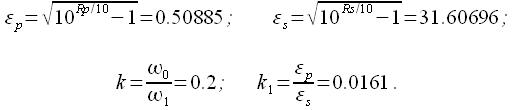
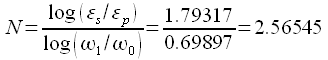

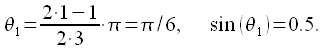
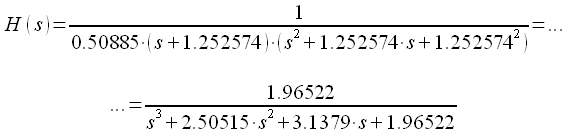
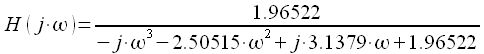
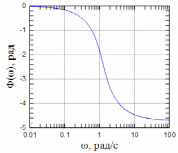 исунок
3: АЧХ рассчитанного фильтра Баттерворта
исунок
3: АЧХ рассчитанного фильтра Баттерворта
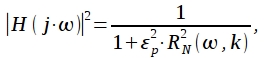
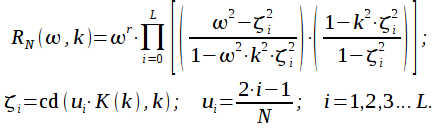
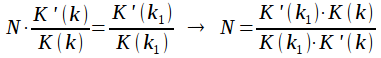
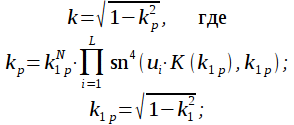
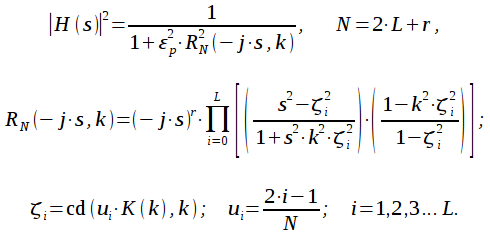

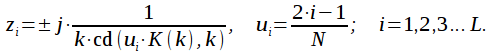


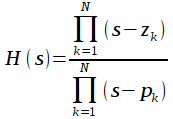

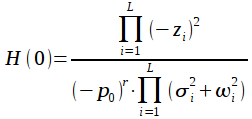
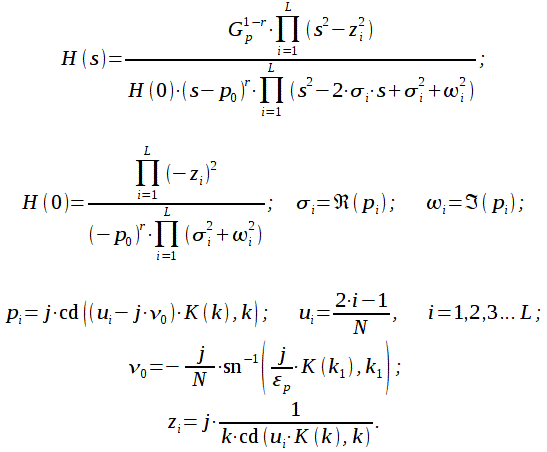
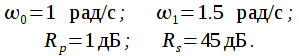
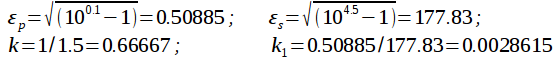
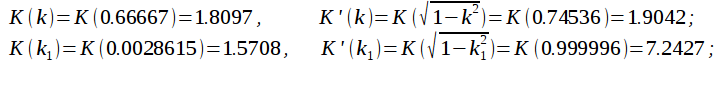


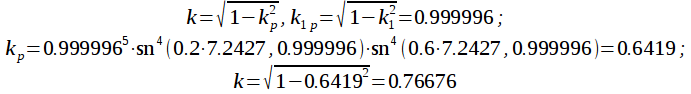
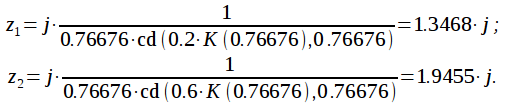

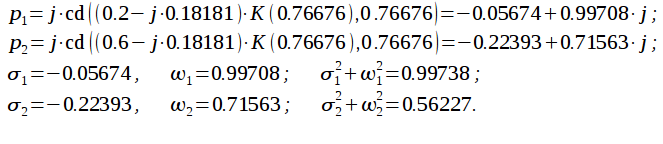

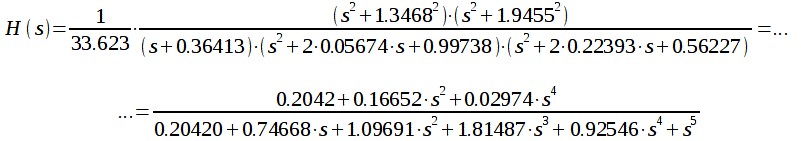
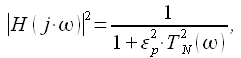
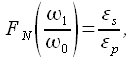
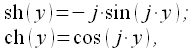

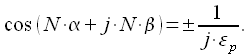
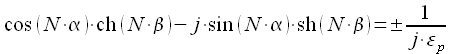
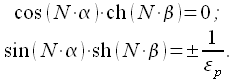

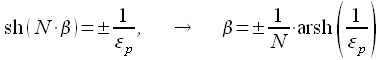
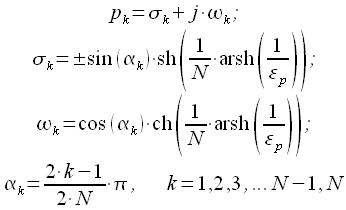

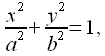
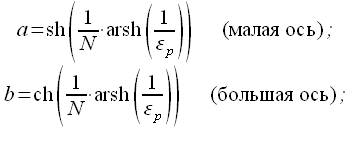
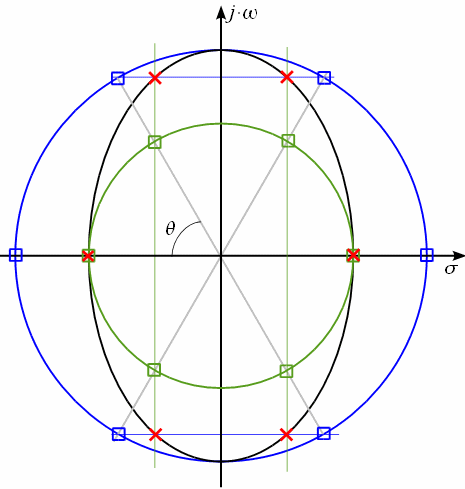

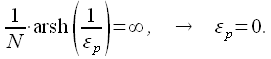
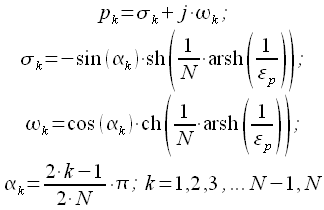
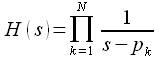

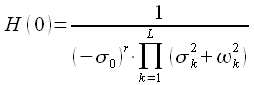

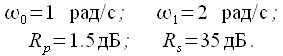

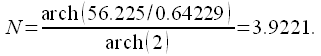
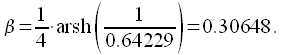
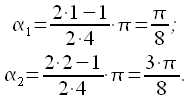

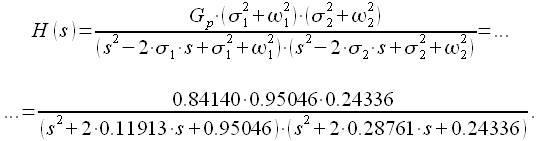
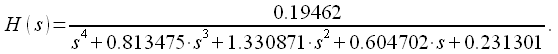
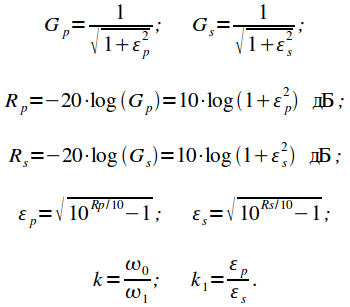

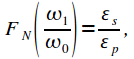
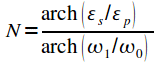

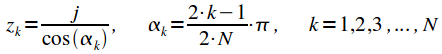
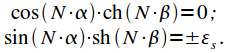

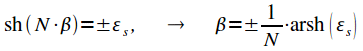
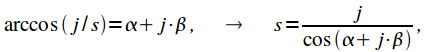

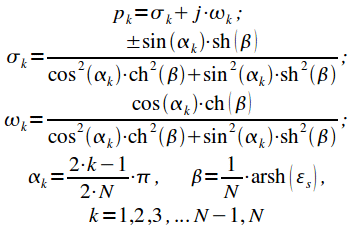
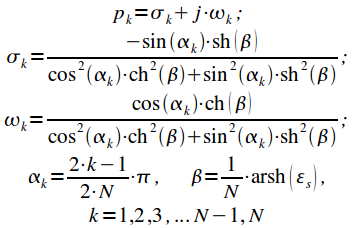
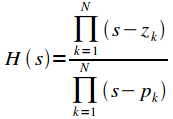
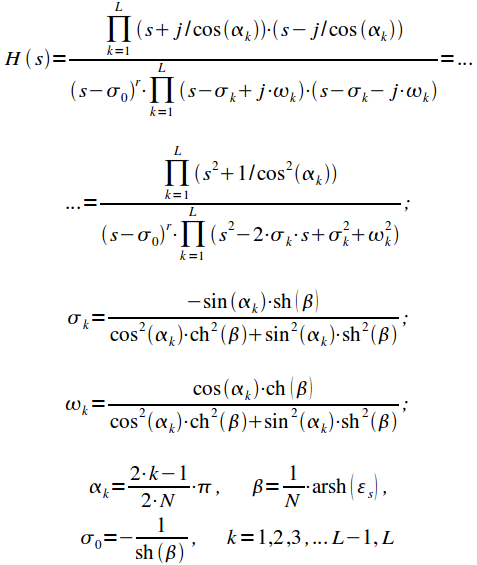

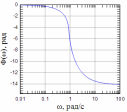
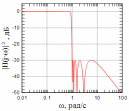
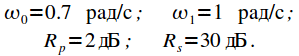

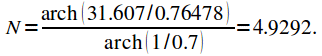
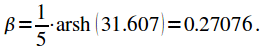
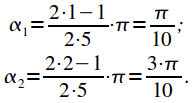
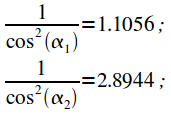
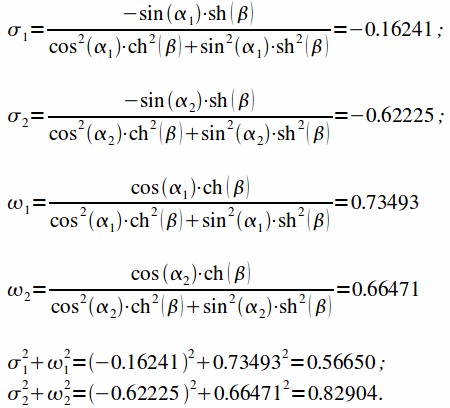

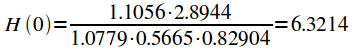
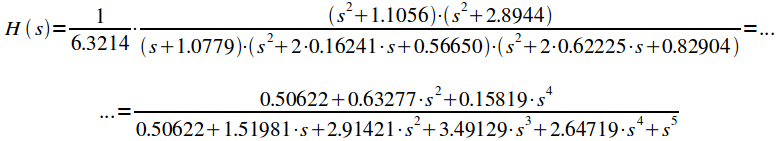
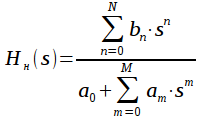

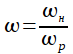
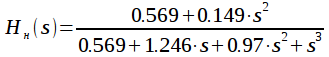
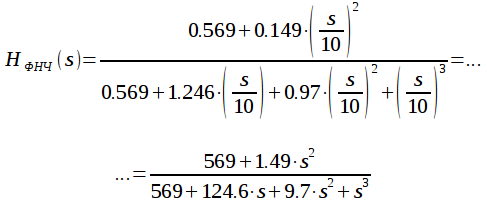

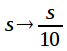
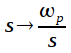
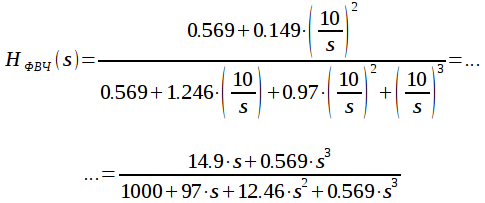

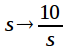

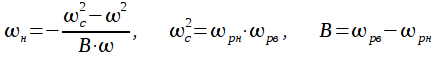


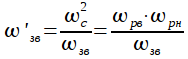
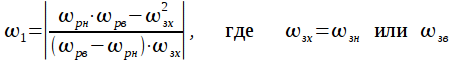
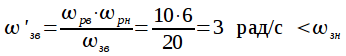

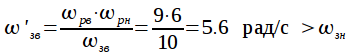
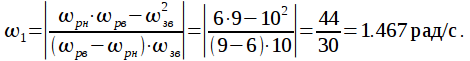
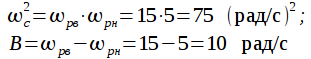
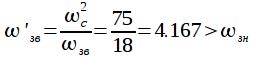
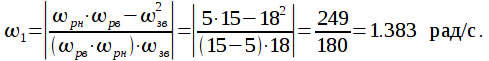

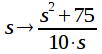
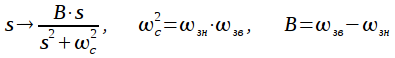

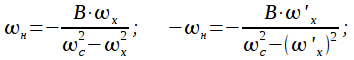
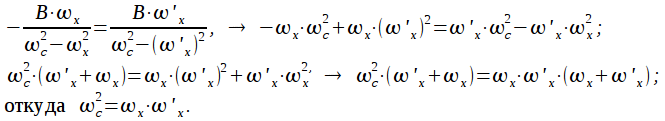
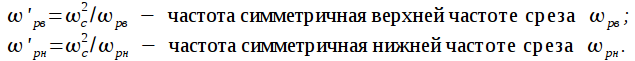
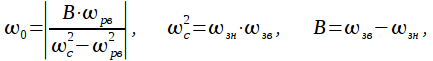


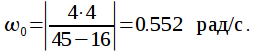



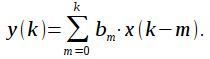

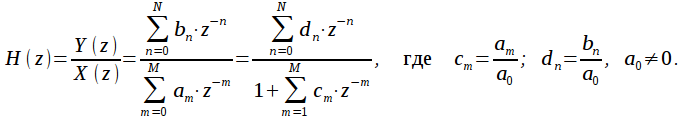

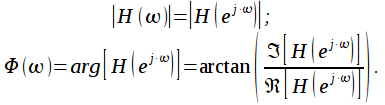
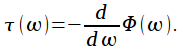
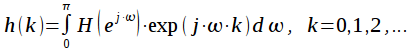 .
.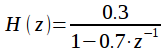 .
.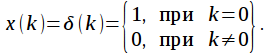
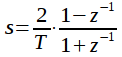


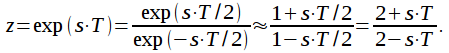
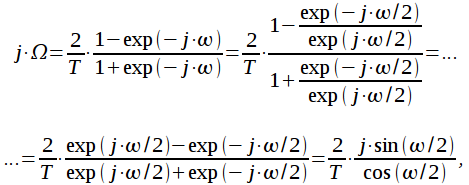
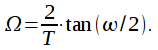
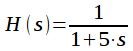

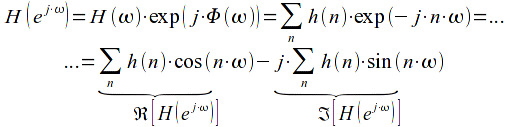
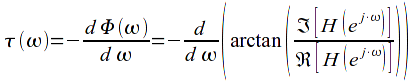
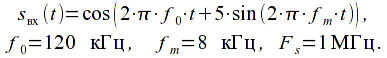
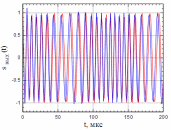
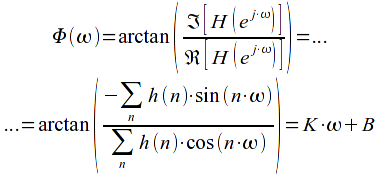
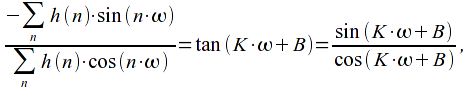

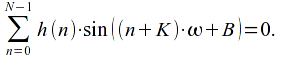
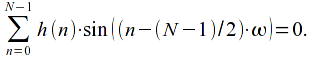
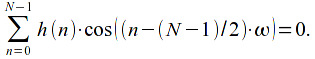
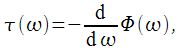
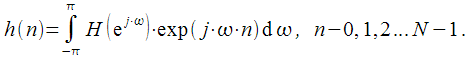




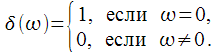
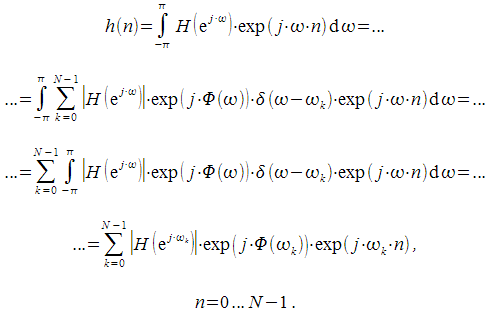

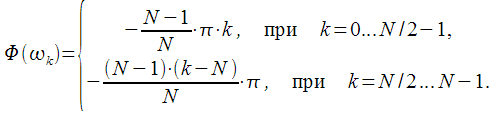
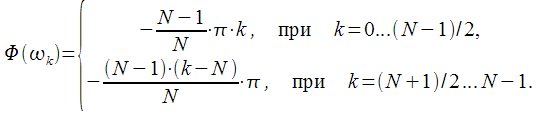
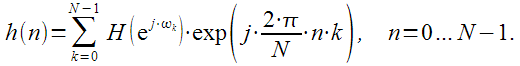
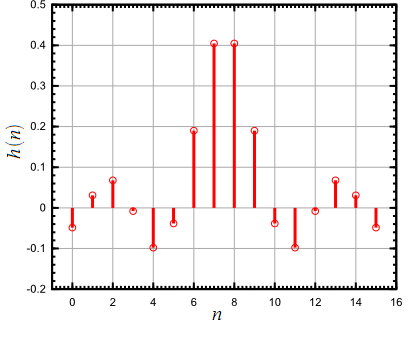 Рисунок
8: Импульсная характеристика рассчитанного
фильтра
Рисунок
8: Импульсная характеристика рассчитанного
фильтра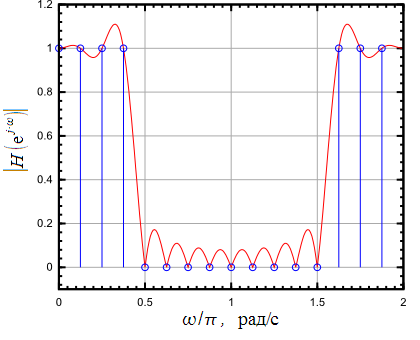 Рисунок
9: АЧХ рассчитанного фильтра точно
проходит через узлы дискретизации
Рисунок
9: АЧХ рассчитанного фильтра точно
проходит через узлы дискретизации