8.3. Уравнения регрессии

Аппроксимация данных с учетом их статистических параметров относится к задачам регрессии. Они обычно возникают при обработке экспериментальных данных, полученных в результате измерений процессов или физических явлений, статистических по своей природе (как, например, измерения в радиометрии и ядерной геофизике), или на высоком уровне помех (шумов). Задачей регрессионного анализа является подбор математических формул, наилучшим образом описывающих экспериментальные данные.

Математическая постановка задачи регрессии заключается в следующем. Зависимость величины (числового значения) определенного свойства случайного процесса или физического явления Y от другого переменного свойства или параметра Х, которое в общем случае также может относиться к случайной величине, зарегистрирована на множестве точек   множеством значений   при этом в каждой точке зарегистрированные значения Y_k и X_k отображают действительные значения Y_k(X_k) со случайной погрешностью  , распределенной, как правило, по нормальному закону. По совокупности значений Y_k требуется подобрать функцию   для которой зависимость Y(X) отображалась бы с минимальной погрешностью.

Функцию   называют регрессией величины y на величину х. Регрессионный анализ предусматривает задание вида функции   и определение численных значений ее параметров a₀, a₁, … , a_n, обеспечивающих наименьшую погрешность приближения к множеству значений Y_k. Как правило, при регрессионном анализе погрешность приближения вычисляется методом наименьших квадратов (МНК).

Виды регрессии обычно называются по типу аппроксимирующих функций: полиномиальная, экспоненциальная, логарифмическая и т.п.

8.3.1. Линейная регрессия

Если разброс точек около предполагаемой кривой зависимости одной величины от другой невелик, то эту зависимость можно определить с помощью МНК, подбирая подходящие параметры этой функции. Если разброс точек велик, то, как правило, достаточно трудно подобрать какую-либо иную функцию, кроме линейной. Такая эмпирическая кривая будет прямой регрессии.

Пусть мы имеем некоторое количество пар точек  ,  . Подберем прямую, проходящую между этими точками, и, в некотором смысле, наилучшим способом аппроксимирующую зависимость Y от  .

Точки (X_k, Y_k), вообще говоря, не лежат на аппроксимирующей прямой. Поэтому  , где   - расстояние по ординате точки (X_k, Y_k) до этой прямой.

Введем в рассмотрение арифметические средние

,

Потребуем, чтобы выполнялось условие  .

Получим  .

Снова будем пользоваться обозначениями центрированных переменных  ,  . Теперь наши исходные уравнения принимают вид  .

Для определения А применим метод наименьших квадратов

,

где, как и раньше,

,

Величина А является коэффициентом регрессии, а уравнение регрессии принимает вид

или  .

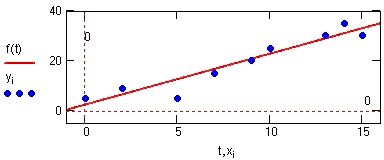
Для построения функции линейной регрессии применяют полином первой степени, т.е. функцию вида   (рис. 8.3.1).

Рис. 8.3.1. Линейная регрессия.

Отклонения точек (X_k, Y_k) от прямой регрессии создают некоторую неопределенность (ошибку) в вычислении коэффициента регрессии А. Для вычисления ошибки А воспользуемся правилами МНК. Нормальным уравнением для МНК-оценки коэффициента регрессии будет  , а остаточные разности суть отклонения Y_k от коэффициента регрессии в точках  .

Вычислим среднеквадратическую ошибку «единицы веса» 

Нужно заметить, что хотя нормальное уравнение содержит одну неизвестную величину, в знаменателе приведенной формулы нужно брать n-2, так как число степеней свободы прямой регрессии две: параллельный перенос и поворот. Степень свободы параллельного переноса мы использовали, выбрав за начало отсчета точку плоскости с координатами  .

Весом неизвестного А является коэффициент [xx] нормального уравнения, поэтому

.

Полученную формулу можно упростить, если ввести в рассмотрение эмпирический коэффициент корреляции. Раскрывая скобки и суммируя, получим

.

Подставим сюда  .

, где  .

Следовательно,  . Обозначим  . Теперь  .

Переменные X и Y в данной задаче равноправны. В отличие от классических задач, в которых используется метод наименьших квадратов, X_k не являются точными значениями аргумента. Несовпадение прямой регрессии с наблюдательными данными в том числе вызвано и погрешностями в определении X_k. Поэтому задачу аппроксимации зависимости этих двух переменных друг от друга можно также решать, как определение линейной зависимости X от  .

Тогда, повторяя приведенные выше выкладки, получим

.

Зависимость Y от X при условии минимизации отклонений Y_k от прямой регрессии, как уже говорилось, называется регрессией y на x. Наоборот, зависимость X от Y называется регрессией x на y. Эти две прямые, вообще говоря, не совпадают.