Примечания
Достоинства:
Вейвлетные преобразования обладают всеми достоинствами преобразований Фурье.
Вейвлетные базисы могут быть хорошо локализованными как по частоте, так и по времени. При выделении в сигналах хорошо локализованных разномасштабных процессов можно рассматривать только те масштабные уровни разложения, которые представляют интерес.
Базисные вейвлеты могут реализоваться функциями различной гладкости.
Недостатки:
Можно выделить один недостаток, это относительная сложность преобразования.
Чирплет
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
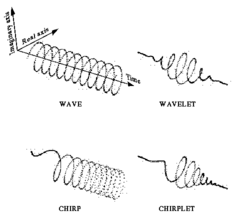
Сопоставление волна(wave)- вейвлет, ЛЧМ-сигнал(chirp)- чирплет
В обработке сигналов чирплет преобразование — это скалярное произведение входного сигнала с семейством элементарных математических функций, именуемых чирплетами.
Содержание
|
Аналогия с другими преобразованиями
Подобно вейвлетам (см. Непрерывное вейвлет-преобразование или Дискретное вейвлет-преобразование), чирплеты получаются из одного материнского чирплета (аналогично «материнскому» или «родительскому» вейвлету в теории вейвлетов).
Чирплеты и чирплет-преобразование
Термин «chirplet transform» был предложен Стивом Манном[1] — он служил заголовком первой опубликованной на эту тему статьи. Само по себе слово «чирплет» использовалось Стивом Манном, Доминго Миховиловичем и Рональдом Брейсвеллом для описания результата применения взвешивающего окна к ЛЧМ-сигналу (англ. chirp). По словам Манна:[2]
Вейвлет — это кусочек волны [wave], а чирплет — соответственно, кусочек ЛЧМ-сигнала [chirp]. Точнее, чирплет — результат умножения такого сигнала на окно, что обеспечивает свойство локализованности во времени. В условиях частотно-временного пространства мелкие ЛЧМ-импульсы существуют как вращающиеся, сдвинутые, деформированные структуры, движущиеся от традиционного параллелизма по временной и частотным осям, типичным для волн (Фурье и оконное преобразование Фурье или вейвлеты).
Таким образом, чирплет-преобразование является повернутым, взвешенным или иначе измененным мозаичным представлением частотно-временной плоскости. Хотя ЛЧМ-сигналы и их приложения известны давно, первая опубликованная работа о «чирплет-преобразовании»[3] описывала особое представление сигналов с помощью семейств функций, связанных друг с другом операторами частотного, временного сдвигов, масштабирования и проч. В этой статье в качестве примера было представлено чирплет-преобразование от Гауссиана, вместе с примером обнаружения льда с помощью радиолокатора (улучшение результатов распознавания цели при применении описанного подхода). Термин «чирплет» (но не «чирплет-преобразование»!) также применялся для схожего преобразования, описанного Миховиловичем и Брэйсвеллом позже в том же году.
Приложения
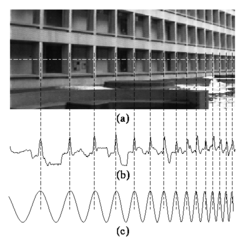
(a) В обработке изображений, период часто изменяется линейно. (b) На этом рисунке повторяющиеся структуры — темные области в окнах и светлые опоры — «сплющиваются» (возрастает частота) при сдвиге вправо. (c) Чирплет преобразование в данном случае более полезно, чем Фурье или вейвлет — преобразования.
Чирплет-преобразование широко применяется в:
радиолокации
медицине
анализ кардиограмм;
анализ ЭЭГ, например Cui, et al..
обработке сигналов
обработке изображений
SETI@home использует ЛЧМ-сигналы (chirp) для компенсации эффекта Допплера.
Chirplet Time Domain Reflectometry (from National Instruments website)