2.4. Векторный фильтр Калмана

В практических ситуациях обычно обнаруживается, что авторегрессивная модель сигнала первого порядка недостаточна для адекватной характеристики физического процесса. Более вероятно, что потребуется AP- процесс N-го порядка. Таким, например, является случай моделирования трактов передачи данных.

Яндекс.ДиректВсе объявленияОптимизация оплаты. Оклады Премии Семинар 26-27.02 в Москве, 11-12.03 в Киеве. Первым лицам скидки до 50%. lityagin.ru  Заработай свои 500-700 у.е./мес. и Получай регулярный доход! Легально. Этично. Надежно. Интересно. Не МЛМ! academyprivateinvestment.com 

Для рассмотрения фильтров высшего порядка, уравнения фильтра Калмана первого порядка, приведенные в разд. 2.3., можно модифицировать путем замены скаляров векторами N-го порядка. Этот процесс лучше всего проиллюстрировать простым примером.

Самым простым будет пример, в котором рассматриваемый авторегрессивный процесс представляется  выражением второго порядка, имеющим вид:

               (2.54)  

Зададим две переменные состояния  и :

и перепишем выражение (2.54) в виде пары уравнений состояния:

       (2.55)

     

Записывая (2.55) в виде матричного уравнения, имеем:

или

                  (2.56)

Уравнения фильтра Калмана для задачи оценивания представлены теперь в векторной форме, но они имеют такой же вид, как и для скалярного фильтра:

        (2.57)

     (2.58)

     (2.59)

     (2.60)

где дисперсия скалярного наблюдаемого шума  и дисперсия шума системы  заменены матрицами   и  соответственно:

Аналогично параметр фильтра, или усиление Калмана, заменен матрицей  порядка .

В разд. 2.4.1 приводится пример использования векторного фильтра Калмана для коррекции при передаче данных. Формат фильтра будет более наглядно проиллюстрирован с помощью этого примера, чем путем задания произвольных обобщенных соотношений для векторного устройства оценивания.

2.4.1. Векторный фильтр Калмана в качестве устройства коррекции канала

Примером, выбранным здесь для иллюстрации действия фильтра Калмана, будет коррекция канала [186]. В случае, когда произвольная последовательность данных передается по искажающему каналу связи, вызывающему межсимвольную интерференцию (МСИ), для восстановления исходной последовательности данных требуется фильтрация или коррекция выходного сигнала канала. Этот пример несколько глубже рассматривается в гл. 8 с точки зрения применения адаптивных фильтров, однако здесь, он использован просто в качестве иллюстрации применения векторной оценки Калмана.

Яндекс.ДиректВсе объявленияОптимизация оплаты. Оклады Премии Семинар 26-27.02 в Москве, 11-12.03 в Киеве. Первым лицам скидки до 50%. lityagin.ru  Играй в новую браузерную ММОРПГ! Инстансы, профессии, увлекательные бои и прокачка персонажа! Регистрируйся! drako.ru 18+

Искажение, вводимое каналом, можно моделировать с помощью фильтра (с весами, обозначенными , вместо ) с линейной импульсной характеристикой  конечной длительности такого же типа, как фильтр, показанный на рис. 2.2, с шумом, добавленным на выходе. Это модель наблюдаемого процесса, показанного на рис. 2.3. Данные на входе канала  имеют случайное распределение, и, следовательно, модель генерации сигнала можно представить в виде:

      (2.61)

      (2.62)

Тогда, наблюдаемый сигнал канала во время выборки с номером , определяется как:

            (2.63)

где - вектор  коэффициентов канала, а - аддитивный шум на выходе канала. Полагая  унитарной матрицей, получаем, что предсказание  становится равным просто  и выражение для корректирующего фильтра Калмана имеет вид:

             (2.64)

а итерации для определяются уравнениями (2.58) – (2.60). Здесь следует отметить, что коэффициенты искажения канала  предполагаются априорно известными.

Корректирующий фильтр, или выравниватель, описываемый уравнением (2.64), схематически изображен на рис. 2.6 а, показывающем, как произведения различных матриц физически обеспечивают формирование предсказания и коррекции. Это можно сравнить с точной многоканальной матричной реализацией, показанной на рис. 2.6. б,

Более распространенным применением методов оценивания Калмана является расчет значений весов ветвей для корректирующих фильтров с конечной импульсной характеристикой  [122]. Обсуждение подобного применения метода Калмана и быстрого метода Калмана приводится в работе [240].

а

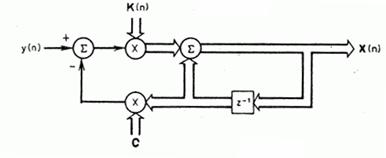
б

Рис. 2.6. а – блок-схема корректирующего фильтра Калмана -го порядка; б – точная реализация векторного фильтра Калмана.

3. Вейвлетный анализ. Чирплетный анализ.

Вейвлет-преобразование (англ. Wavelet transform) — интегральное преобразование, которое представляет собой свертку вейвлет-функции с сигналом.

Cпособ преобразования функции (или сигнала) в форму, которая или делает некоторые величины исходного сигнала более поддающимися изучению или позволяет сжать исходный набор данных. Вейвлетное преобразование сигналов является обобщением спектрального анализа. Термин (англ. wavelet) в переводе с английского означает "маленькая волна". Вейвлеты — это обобщённое название математических функций определенной формы, которые локальны во времени и по частоте и в которых все функции получаются из одной базовой, изменяя её (сдвигая, растягивая).

Содержание 1 Требования к вейвлетам 2 Свойства вейвлет преобразования 3 Непрерывное вейвлет-преобразование 4 Дискретное вейвлет-преобразование 5 Графическое представление 6 Применение 7 Примечания 8 См. также 9 Литература 10 Ссылки