2.3.1 Скалярный фильтр Калмана

По существу,  устройство калмановской оценки реализует процесс параметрического оценивания, основанный на авторегрессивной (АР) модели процесса генерации сигнала. АР-модель процесса первого порядка данного типа показана на рис. 2.3, а, а соответствующая модель измерений – на рис. 2.3, б. 

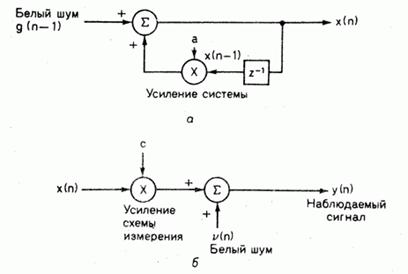
Рис. 2.3. а – рекурсивная модель генерации сигнала первого порядка; б – модель схемы измерения данных

Модель измерений представляет просто усилительное звено и источник аддитивного  белого шума . Приняв эту модель генерации сигнала, поступающую выборку сигнала с номером можно определить как

           (2.27)

Рекурсивная формула оценки первого порядка имеет вид

           (2.28)

Отметим, что в (2.28) коэффициенты передачи усилительных звеньев фильтра зависят от времени (структурная схема этого устройства оценки в общем виде показана на рис. 2.4).

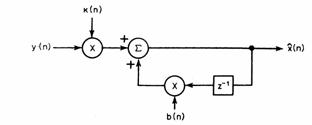
Рис. 2.4 Обобщенная структурная схема рекурсивного устройства оценки первого порядка

Для получения оптимального (с точки зрения метода наименьших квадратов) устройства оценки среднеквадратичная ошибка  дифференцируется по  и , а результаты приравниваются к нулю:

        (2.29)

       (2.30)         

            (2.31)

Соотношение между  и  можно вывести, воспользовавшись (2.30):

                 (2.32)

 

              (2.33)

Подставив значение из (2.27), находим

  .   (2.34)

Для оптимального устройства оценки должен выполняться принцип ортогональности, который приводит к следующим соотношениям:

     

Тогда уравнение (2.34) примет вид

               (2.35)

Из нашей модели генерации сигнала имеем

          (2.36)

Подставляя (2.36) в (2.35), получаем 

          (2.37)

Из уравнений (2.27) и (2.28) находим

         (2.38)

а подстановка из (2.36) дает:

                  (2.39)

и поскольку среднее всех произведений членов (2.39) на  равно нулю, можем записать

Воспользовавшись этим соотношением, преобразуем (2.37):

             (2.40)

Это приводит к окончательному соотношению между  и :

               (2.41)

Подставляя (2.41) в (2.28), находим

            (2.42)

Уравнение (2.42) является определением оптимального рекурсивного устройства оценки первого порядка или скалярного фильтра Калмана. Первый член  предсказывает текущую выборку, а второй член корректирует на основании оценки ошибки с учетом калмановского коэффициента . Структура такого фильтра иллюстрируется на рис. 2.5.

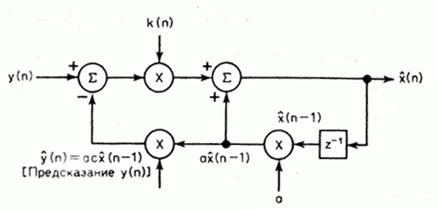
Рис. 2.5. Блок-схема скалярного фильтра Калмана первого порядка.

2.3.2. Вывод коэффициента фильтра Калмана

Яндекс.ДиректВсе объявления Библиотека диссертаций РГБ Электронная библиотека диссертаций из РГБ, все научные специальности. dissercat.com  Научная библиотека диссертаций Электронная библиотека диссертаций. Доставка из РГБ 10 мин. Цена 480р. dslib.net 

Определив структуру фильтра Калмана, необходимо получить выражения для изменяющегося во времени коэффициента усиления Калмана . Сначала, подставляя (2.28) в (2.29) , определим среднеквадратичную ошибку в виде

                                                                 (2.43)

                                                                                                                      (2.44)

Используем (2.27) вместо для подстановки в (2.44):

                                                                                               (2.45)

Подставляя (2.45) в (2.44), находим:

                                                                                                              (2.46)

           

Раскрывая  и, используя  выражение (2.28) для , получаем:

                                                                               (2.47)

                                                                                                                           (2.48)

где . Теперь, подставляя (2.42) в выражение для среднеквадратичной ошибки (2.29), имеем:

                                                          (2.49)

а используя (2.27) и (2.36), находим:

                                       (2.50)

                                                               (2.51)

Подстановка (2.47) в (2.51) дает:

                                                                                      (2.52)

Отметим, что сначала, зная  , надо рассчитать , а затем уже   по формуле:

                                                                                                           (2.53)

Три уравнения: (2.42), (2.52) и (2.53) – являются рекурсивными уравнениями, необходимыми для реализации фильтра Калмана первого порядка. В отличие от фильтра Винера, усиление фильтра Калмана должно быть выражено итерационным соотношением, а, следовательно, его нельзя представить в виде универсального стационарного решения.