43 (8). Основы комбинаторики: соединения, правила сложения и умножения, перестановки, сочетания, размещения.

Группы, составленные из каких-либо предметов, например, букв, чисел, геометрических фигур, цветных флажков и т. п., называются соединениями. Сами предметы, из которых составляются соединения, называются элементами. Различают три основных типа соединений: размещения, перестановки и сочетания.

Размещения 

А из n по m элементов — соединения, отличающиеся самими элементами или их порядком.

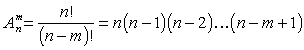
Перестановки 

Р — соединения, отличающиеся только порядком элементов.

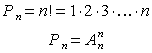
Сочетания 

С из n по m элементов — соединения, отличающиеся только самими элементами.

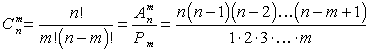
Правило сложения (правило «или») — одно из основных правил комбинаторики, утверждающее, что, если элемент A можно выбрать n способами, а элемент B можно выбрать m способами, то выбрать A или B можно n + m способами.

Правило умножения (правило «и») — одно из основных правил комбинаторики. Согласно ему, если элемент A можно выбрать n способами, и при любом выборе A элемент B можно выбрать m способами, то пару (A, B) можно выбрать n·m способами. Естественным образом обобщается на произвольную длину последовательности.

44 (9). Равновозможные события. Классическое определение вероятности. Частота события. Статистическое определение вероятности. Геометрическое определение вероятности.

Если при проведении опыта могут произойти несколько событий и каждое из них по объективным условиям не является более возможным, чем другое, то такие события называются  равновозможными. Примеры равновозможных событий: появление двойки, туза и валета при вынимании карты из колоды, выпадение любого из чисел от 1 до 6 при бросании игральной кости и т.п

Классическое определение вероятности

Предположим, что мы имеем дело с пространством элементарных исходов, состоящим из конечного числа   элементов:  . Предположим, что из каких-либо соображений мы можем считать элементарные исходы равновозможными. Тогда вероятность любого из них принимается равной  . Эти соображения не имеют отношения к математической модели и основаны на какой-либо симметрии в эксперименте (симметричная монета, хорошо перемешанная колода карт, правильная кость).

Если событие   состоит из   элементарных исходов, то вероятность этого события равняется отношению  :

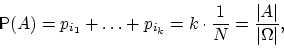
где символом   обозначено число элементов конечного множества  .

Говорят, что эксперимент удовлетворяет классическому определению вероятности, если пространство элементарных исходов состоит из конечного числа   равновозможных исходов. В этом случае вероятность любого события   вычисляется по формуле

называемой классическим определением вероятности.

Частота события   — отношение   числа   наступлений этого события в   испытаниях к числу испытаний  .

Статистической вероятностью события А называется относительная частота появления этого события в произведенных испытаниях, т. е. . где                                                                     (1.2)  - статистическая вероятность события А w(A)  - относительная частота наступления события А m -  число испытаний, в которых появилось событие А n  - общее число испытаний.

В отличие от классического определения вероятности, статистическое определение является опытной, экспериментальной характеристикой.

Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области, т.е. .