11. Бесконечно малые функции. Сравнение бесконечно малых.

Опр. Ф-ция (х) наз-ся б/м в т.х₀, если ее предел в этой т-ке равен 0 из этого определения вытекает следующее св-во б/м ф-ций:

а) Алгебраическая сумма и произведение б/м ф-ций есть б/м ф-ции.

б) Произведение б/м ф-ции на ограниченную ф-цию есть б/м ф-ция, т.е. если (х)0 при хх0, а f(x) определена и ограничена ( С:(х)С)=> (х)(х)0 при хх0

Если отношение 2-х б/м (х)/(х)0 при хх₀ то говорят что б/м  имеет более высокий порядок малости чем .

Если (х)/(х)с,с0 при хх₀ (с-число), то (х) и (х) наз-ся б/м одного порядка.

если (х)/(х)1 , то (х) и (х) наз-ся эквивалентными б/м ((х)~(х)), при хх₀.

Аналогичные определения для случаев: хх₀-, хх₀+, х-, х+ и х.

12. Эквивалентные бесконечно малые функции.

Опр. БМФ (х) и (х) называются эквивалентными в точке х₀, если предел их отношения в этой точке=1. (х) ~ (х), lim(x->x₀₎ (х)/(х)=1.

Т1. Предел отношения БМФ в точке х₀ функции не изменится, если каждую из них заменить на эквивалентную её в точке х₀ функцию.

13. ББФ

Опр. Ф-ия y=f(x) называется бесконечно большой в точке х₀, если ее предел в этой точке равен бесконечности. (f(x)-б-б)=lim(x->х₀)(f(x))=∞).

1. Произведение двух бесконечно больших ф-ий – бесконечно большая ф-ия.

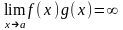
2. Произведение бесконечно больших на ф-ию, имеющую отличный от нуля предел - бесконечно большая.

3. Ф-я, обратная величине бесконечно большой – есть бесконечно малая, и наоборот.

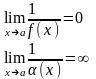
14.Непрерывность функции в точке.

Пусть функция f(x) определена в некоторой окрестности точки x0.

Определение 1. Функция f(x) называется непрерывной в точке x0, если предел функции и ее значение в этой точке равны, т. е. ₀)

Функция f(x) называется непрерывной на множестве Х,если она непрерывна в каждой точке множества.

Функция f(x) называется непрерывной на отрезке[а;б],если она непрерывна в каждой точке внутри интервала (а,б),непрерывна слева в т.б,и справа в т.а.

15. Арифметические операции над непрерывными функциями. Непрерывность сложной и обратной функции.

Т1. Пусть ф-ии f(x) и g(x) непрерывны в точке x₀. Тогда ф-ии f(x)±g(x), f(x)*g(x), f(x)/g(x)(g(x₀)≠0) также непрерывны в точке х₀.

Т2. Пусть дана f:x->y, непрерывна в точке х₀€Х.

Пусть у₀=f(x₀)

Пусть g: y z, непрерывна в точке у₀.

Тогда сложная ф-ция g(f(x)) непрерывна в точке x₀.

Следствие: любая элементарная функция непрерывна в своей области определения.

Т3. Пусть ф-ция y=f(x)возрастает(убывает) на отрезкe[a;b] и пусть α=f(a )иβ=f(b). Пусть f(x)непрер.на [α;β], тогда существует обратная ф-ция x=f^-1(y) определённая и непрерывная на отрезке [α;β]( [β;α]).

β

у α

α

β

а х b а b