13

Министерство образования и науки РФ

Рязанский государственный университет имени С.А. Есенина

Исследовательская работа по математической логике

«Равносильность формул логики высказываний. Равносильные преобразования.»

Выполнила

студентка 2 курса группы 3108

физико-математического факультета

Бакина Юлия

Проверила: Солонина А.Г.

Рязань 2013

Содержание

Введение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2

Цели работы и задачи. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1. Определение равносильных формул. . . . . . . . . . . . . . . . .4

2. Важнейшие равносильности алгебры логики . . . . . . . . .5

3. Некоторые из важнейших равносильностей алгебры

другими словами. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .8

4. Равносильные преобразования. . . . . . . . . . . . . . . . . . . . . 9

5.Принцип двойственности. . . . . . . . . . . . . . . . . . . . . . . . . . .10

Заключение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

Список использованной литературы. . . . . . . . . . . . . . . . . . .12

Введение

Логика (др. греч. λογική — «наука о рассуждении», «искусство рассуждения» от λόγος — «речь», «рассуждение», «мысль») — это наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Логика состоит из большого числа логических систем. Эти системы принято делить на классическую логику, включающую классические логику высказываний и логику предикатов, и неклассическую логику.

Как самостоятельная наука логика сложилась в IV в. до н.э. Ее основателем по праву считается древнегреческий философ Аристотель (384-322 гг до н.э.).В своих научных трудах Аристотель впервые дал ее систематическое изложение и назвал “традиционной” формальной логикой. Основным содержанием аристотелевской логики является теория дедукции, но в его трудах также прослеживаются начала исчисления высказываний. Логика высказываний - раздел логики, в котором вопрос об истинности или ложности высказываний решается на основе изучения способа построения высказываний из элементарных (далее не разлагаемых и не анализируемых) с помощью логических связок. Логику высказываний называют также исчислением высказываний. Высказыванием называется всякое утверждение (повествовательное предложение), про которое всегда определенно и объективно можно сказать, является ли оно истинным или ложным.

В данной работе рассмотрим равносильность формул и равносильные преобразования логики высказываний.

Цель работы:

Сравнить и исследовать определения равносильности, взятые из нескольких источников. Выяснить, какое из определений является наиболее доступным для изучения.

Задачи:

-выяснить, что такое равносильные формулы и преобразования;

-рассмотреть важнейшие равносильности алгебры логики;

-применить равносильные преобразования на практике.

1.Определение равносильных формул

В пособии Л.В. Балабко «Алгебра логики» определение выглядит так:

Определение. Две формулы алгебры логики А и В называются равносильными, если они принимают оди­наковые логические значения на любом наборе значе­ний входящих в формулы элементарных высказыва­ний.

Равносильность формул будем обозначать знаком  , а запись А  В означает, что формулы А и В рав­носильны.

В учебнике И.Л. Никольской «Математическая логика» определение излагается следующим образом:

Определение. Формулы F1 и F2 называются равносильными, если их эквиваленция F1↔ F2 является тавтологией.

Эквиваленция истинна тогда и только тогда, когда составляющие её высказывания оба истинны либо оба ложны; следовательно, F1↔ F2 есть тавтология только в том случае, если формулы F1 и F2 «одновременно», т.е. при одинаковых наборах значений переменных, входящих в формулы, принимают одинаковые значения.

2. Важнейшие равносильности алгебры логики

Рассмотрим важнейшие равносильности алгебры логики, которые можно разбить на три основные группы.

I группа. Основные равносильности .

1) x ÙЩ x ºє x; x ÚЪ x ºє x – законы идемпотентности;

2) x ÙЩ 1 ºє x; x ÚЪ 1 ºє 1;

3) x ÙЩ 0 ºє 0; x ÚЪ 0 ºє x;

4. xºє x – закон тождества;

x ÙЩ``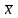 ºє 0 – закон противоречия;

x ÚЪ`` ºє 1 – закон исключения третьего;

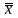4. ºє x – закон снятия двойного отрицания;

6) x ÙЩ (x ÚЪ y) ºє x; x ÚЪ (x ÙЩ y) ºє x – законы поглощения.

Доказать справедливость каждого тождества можно, построив таблицы истинности. Например, докажем справедливость закона поглощения относительно дизъюнкции. Таблица истинности будет содержать 4 строки:

х	у	уvx	хÙЩ(уvx)
0	0	0	0
1	0	1	1
0	1	1	0
1	1	1	1

Сравнивая значения последнего столбца с соответствующими значениями высказывания х можно сделать вывод о справедливости тождества.

II группа. Равносильности, выражающие одни логические операции через другие.

1) x ®® y ºє`` ÚЪ y;

2) x «« y ºє (x ®® y) ÙЩ (y ®® x);

3) Закон де Моргана (закон инверсии или отрицания):

4) и 5) тождества докажем, применив закон двойного отрицания и тождества 3) второй группы:

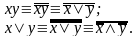
III группа. Основные законы алгебры логики.

1) коммутативность:

x ÙЩ y ºє y ÙЩ x,

x  y  y  x;

2) ассоциативность:

x ÙЩ (y ÙЩ z) ºє (x ÙЩ y) ÙЩ z

x ÚЪ (y ÚЪ z) ºє (x ÚЪ y) ÚЪ z

3) дистрибутивность:

x ÙЩ (y v z) ºє x ÙЩ y ÚЪ x ÙЩ z – относительно дизъюнкции,

x ÚЪ (y ÙЩ z) ºє (x ÚЪ y) ÙЩ (x ÚЪ z) – относительно конъюнкции.

Докажем справедливость дистрибутивности относительно конъюнкции. Составим таблицу истинности, которая содержит 2³ = 8 строк:

х	у	z	yz	x v yz	x v y	x v z	(x v y)( x v z)
0	0	0	0	0	0	0	0
1	0	0	0	1	1	1	1
0	1	0	0	0	1	0	0
0	0	1	0	0	0	1	0
1	1	0	1	1	1	1	1
0	1	1	1	1	1	1	1
1	0	1	0	1	1	1	1
1	1	1	1	1	1	1	1