4. Структура сапр

Структура систем представляет собой совокупность взаимосвязей между элементами, имеющими определенные характеристики, которые и определяют функционирование системы. Составными структурными частями САПР являются подсистемы, в которых при помощи специализированных комплексов средств

решается функционально законченная последовательность задач проектирования. Укрупненная структура САЙР приведена на рис.12.2. \

По назначению различают подсистемы проектирующие и обслуживающие. Проектирующие подсистемы непосредственно выполняют проектные процедуры. Они имеют объектную ориентацию и реализуют определенный этап (стадию) проектирования или группу непосредственно связанных проектных / задач, примерами проектирующих подсистем могут служить подсистемы геометрического трехмерного моделирования объектов, эскизное проектирование изделий, изготовления конструкторской документации, проектирование технологических процессов механической обработки.

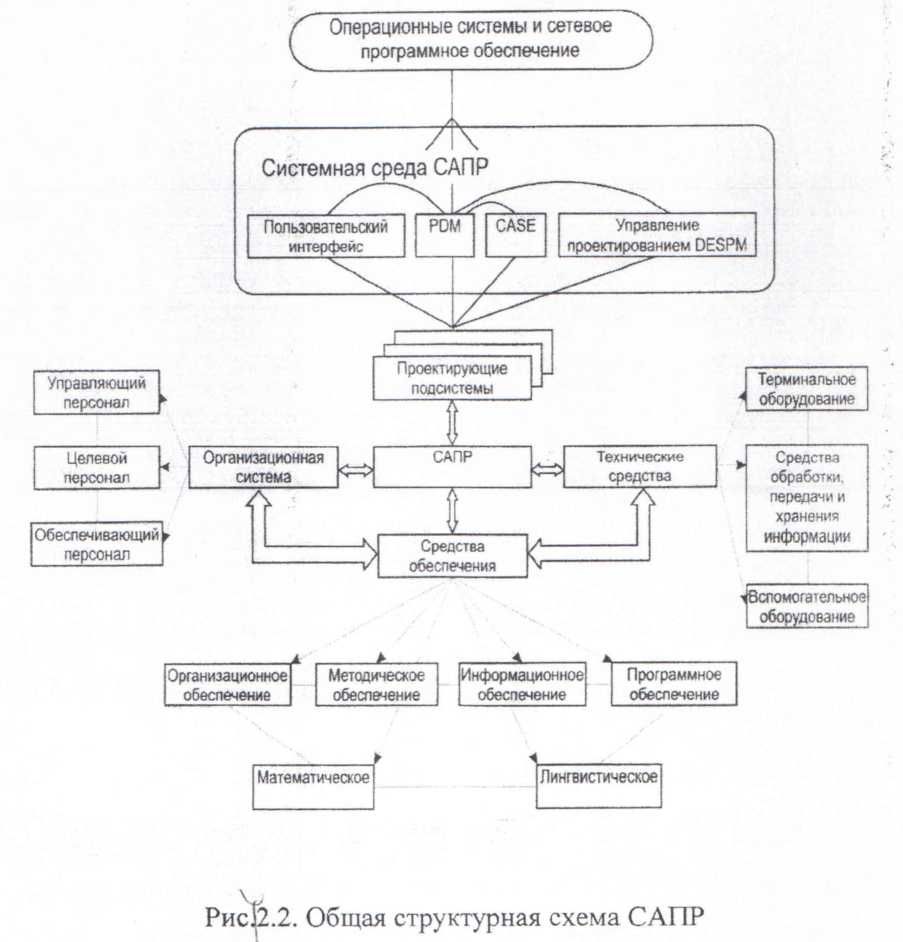
Обслуживающие подсистемы. Такие подсистемы имеют общесистемное применение и обеспечивают функционирование проектирующих подсистем, а также оформление, передачу и вывод полученных в них результатов. Их совокупность часто называют системной средой (или оболочкой) САПР. Типичными обслуживающими подсистемами являются подсистема управления проектными данными (PDM - Product Data Management), управления процессом проектирования (DesPM-Design Process Management), пользовательского интерфейса, подсистема^разработки и сопровождения программного обеспечения •^SUSP-CASE (Computer Aided Software Engineering), автоматизированные банки данных, подсистемы документирования, обучающие подсистемы для освоения пользователями технологий, реализованны¹/САПР. 7 Организационную систему составляют:

• целевой персонал (пользователи), выполняющие действия по проектировани ю, конструированию и технологической подготовке производства;

• управляющий персонал, выполняющий административные функции по управлению, организации и контролю за деятельностью системы в целом;

• обеспечивающий персонал - обеспечивает нормальное функционирование и снабжение комплекса технических средств.

Структурирование средства автоматизации проектирования по различным аспектам обусловливают появление видов обеспечения САПР. Принято выделять

5. Виды обеспечений сапр

Структурирование САПР по различным аспектам обусловливает появлени! видов обеспечения автоматизированного проектирования.

1. Математическое обеспечение

Математическое обеспечение (МО) - методы, математические модели ъ алгоритмы выполнения процесса проектирования. Элементы математическогс обеспечения в САПР чрезвычайно разнообразны. Среди них имеютс? инвариантные элементы, широко применяемые в различных САПР. К ним относятся принципы построения функциональных моделей, методы численногс решения алгебраических и дифференциальных уравнений, постановки экстремальных задач. Специфика предметных областей проявляется прежде всего в математических моделях проектируемых объектов. Формы представления математического обеспечения также довольно разнообразны, но его практическое использование происходит после реализации в программном обеспечении. Разработка математического обеспечения является самым сложным этапом создания САПР, от которого в наибольшей степени зависят производительность и эффективность функционирования системы в целом. Математическое обеспечение САПР должно описывать во взаимосвязи объект, процесс и средства автоматизации проектирования.

По назначению и способам реализаций МО САПР делится на две части:

• математические методы и построенные на их основе математические модели, описывающие объекты проектирования; *

• формализованное описание^лроцедур автоматизированного проектирования. Способы и средства реализации первой части математического обеспечения наиболее специфичны в различных САПР и зависят от особенностей объектов проектирования. Что касается второй части математического обеспечения, то формализация всего процесса автоматизированного проектирования более сложная задача, чем алгоритмизация и программирование отдельных проектных задач.

Математические модели (ММ). В автоматизированных проектных процедурах вместо еще не существующего проектируемого объекта оперируют некоторым квазиобъектом - моделью, которая отражает некоторые интересующие исследователя свойства объекта. Модель может быть физическим объектом (макет, стенд) или спецификацией. Среди моделей-спецификаций различают упомянутые выше функциональные, поведенческие, информационные, структурные модели (описания). Эти модели называют математическими, если они формализованы средствами аппарата и языка математики.

Математические модели служат для описания свойств объектов в процедурах АП. Если проектная процедура включает создание ММ и оперирование ею с целью получения информации об объекте, то говорят, что процедура выполняется на основе математического моделирования.

К математическим моделям предъявляются требования универсальности адекватности, точности и экономичности.

Степень универсальности ММ характеризует полноту отображения в модел] свойств реального объекта, широту класса объектов проектирования, для которые она может быть использована. Как правило, ММ, описывающая формализованный процесс функционирования объекта, охватывает толькс основные (некоторые) свойства (закономерности) объекта, оставляя в стороне несущественные второстепенные факторы. Однако, с ее помощью можно определять и предсказывать последствия изменения реальной системы (объекта) или отдельных ее элементов.

Так, большинство ММ, используемых при функциональном проектировании, предназначено для отображения протекающих в объекте физических или информационных процессов, при этом не требуется, чтобы ММ описывала такие свойства объекта, как геометрическая форма составляющих его элементов.

Точность ММ оценивается степенью совпадения (рассогласования) между вычислительными, рассчитанными с помощью оцениваемой ММ и реальными параметрами объекта. Обычно за реальные (истинные) характеристики принимают результаты экспериментальных измерений, которые, в свою очередь, содержат погрешности постановки и реализации эксперимента.

Пусть отображаемые в ММ свойства оцениваются вектором выходных параметров Y = (yi ,уг ,..., у_т). Тогда, обозначив истинное и рассчитанное с помощью ММ значения у-го выходного параметра через _у/_ист и y_jm соответственно, определим относительную погрешность е₎ расчета параметра^

Получена векторная оценка £j — (s₁,£₂,...,E_m). При необходимости сведения этой оценки к скалярной используют какую-либо норму вектора s, например

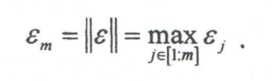
Адекватность ММ — способность отражать заданные свойства объекта с погрешностью не выше заданной. Поскольку выходные параметры являются функциями векторов параметров внешних Q и X; Обычно значения внутренних параметров ММ определяют и^, условия минимизации погрешности е_га в некоторой точке Q_HOm пространства внешних переменных, а используют модель с рассчитанным вектором X при различных значениях Q. При этом, как правило, адекватность модели имеет место лишь в ограниченной области изменения внешних переменных - области адекватности (ОА) ММ

где 6>0 - заданная константа, равная предельно допустимой погрешности модели.

Экономичность ММ характеризуется затратами вычислительных ресурсе (затратами машинного времени Т_м и памяти П_м ) на ее реализацию. Чем меньш Т_м и П_м , тем модель экономичнее. Вместо значений Т_м и П_м , зависящих не тольк от свойств модели, но и от вычислительной мощности компьютера, част используют другие величины, например: среднее количество операций выполняемых при одном обращении к модели, размерность системы уравнений количество используемых в модели внутренних параметров и т.п.

Требования высоких точности, степени универсальности, широкой облает! адекватности, с одной стороны, и высокой экономичности, с другой стороны противоречивы. Наилучшее компромиссное удовлетворение эти? противоречивых требований зависит от особенностей решаемых задач иерархического уровня и аспекта проектирования применяемых ЭВМ. Этс обстоятельство обуславливает применение в САПР широкого спектра математических моделей.

Классификация математических моделей

Классификация математических моделей. Основные признаки классификации и типы математических моделей, применяемые в САПР, даны в табл. 2.1.

Признак классификации	Математические модели (тип)
1. Характер отображаемых свойств объекта	Структурные; функциональные
2. Принадлежность к иерархичес­кому уровню	Микроуровня; макроуровня; метауровня
3. Степень детализации описания внутри одного уровня	Полные; макромодели
4. Способ представления свойств объекта	Аналитические, алгоритмические, имитационные
5. Способ получения модели	Теоретические, эмпирические

Таблица 2.1

По характеру отображаемых свойств объекта ММ делятся на структурные и функциональные.

Структурные ММ предназначены для отображения структурных свойств объекта. Различают структурные ММ топологические и геометрические.

В топологических ММ отображается состав и взаимосвязи элементов объектов. Их чаще всего применяют для описания объектов, состоящих из большого числа элементов, при решении задач привязки конструктивных элементов к определенным пространственным позициям (задачи компоновки оборудования, размещения деталей) или к относительным моментам времени (например, при разработке расписаний, технологических процессов). Топологические модели могут иметь форму графов, таблиц (матриц), списков и т.д.

В геометрических ММ отображаются геометрические свойства объектов, т.е. дополнительно к сведениям о взаимном расположении элементов в них содержатся сведения о форме деталей. Геометрические ММ могут выражаться совокупностью уравнений линий и поверхностей; алгебраических соотношений, описывающих области, составляющие тело объекта; графами и списками, отображающими конструкции из типовых конструктивных элементов, и т.п. Геометрические ММ применяют при решении задач конструирования в машиностроении, для оформления конструкторской документации при задании исходных данных на разработку технологических процессов изготовления деталей. Используют несколько типов геометрических ММ.

В машиностроении для отображения геометрических свойств деталей со сравнительно несложными поверхностями применяют ММ, представляемые в аналитической или алгебраической форме. Аналитические ММ - уравнение поверхностей и линий, например, уравнение плоскости имеет вид ax+by+cz+d^О, эллипсоида - (x/a)²+(y/bf+(z/c) +d= 0, где x,y,z - пространственные координаты, а, Ь, с, d - коэффициенты уравнений. В алгебраических ММ тела описываются системами логических выражений, отражающих условия принадлежности точек внутренним областям тел.

Для сложных поверхностей аналитические и алгебраические модели оказываются слишком громоздкими, их трудно получать и неудобно использовать. Область их применения обычно ограничивается поверхностями плоскими и второго порядка. Для отображения геометрических свойств деталей со сложными поверхностями применяют каркасные и кинематические ММ.

Каркасные ММ представляют собой каркасы - конечные множества элементов, например точек или кривых, принадлежащих моделируемой поверхности. В частности, выбор каркаса в виде линий, образующих сетку на описываемой поверхности, приводит к разбиению поверхности на отдельные участки. Кусочно-линейная аппроксимация на этой сетке устраняет главный недостаток аналитических моделей, так как в пределах каждого из участков, имеющих малые размеры, возможна удовлетворительная по точности аппроксимация поверхностей простыми уравнениями. Коэффициенты этих уравнений рассчитываются исходя из условий плавности сопряжений участков. В кинематических ММ поверхность представляется в параметрическом виде R (u,v), где R—(x,y,z), а и и v - параметры. Такую поверхность можно получить как результат перемещения в трехмерном пространстве кривой R(u), называемой образующей, по некоторой направляющей линии. Коэффициенты уравнений во всех рассмотренных моделях, как правило, не имеют простого геометрического смысла, что затрудняет работу с ними в интерактивном режиме. Этот недостаток устраняется в канонических моделях и в геометрических макромоделях.

Канонические модели используют в тех случаях, когда удается выделить параметры, однозначно определяющие геометрический объект и в то же время имеющие простую связь с его формой. Например, для плоского многоугольника такими параметрами являются координаты вершин, для цилиндра —

направляющие косинусы и координаты некоторой точки оси, а также радиу< цилиндра.

Геометрические макромодели являются описаниями предварительш отобранных типовых геометрических фрагментов. Такими фрагментами могу: быть типовые сборочные единицы, а их макромодели - условные номера габаритные и стыковочные размеры. При оформлении конструкторской документации макромодели используют для описания типовых графически? изображений: зубчатых колес, винтовых соединений, подшипников и т.д.

Функциональные ММ предназначены для отображения физических и или информационных процессов, протекающих в объекте при его функционировании или изготовлении. Математическая функциональная модель в общем случае представляет собой алгоритм вычисления вектора выходных параметров Y при заданных векторах параметров элементов X и внешних параметров Q. Обычно функциональные ММ представляют собой системы уравнений, связывающих фазовые переменные, внутренние, внешние и выходные параметры.

Деление описаний объектов на аспекты и иерархические уровни непосредственно касается функциональных математических моделей. Выделение аспектов описания приводит к выделению моделей электрических, механических, гидравлических, оптических, химических и т.п., причем модели процессов функционирования изделий и модели процессов их изготовления различны.

Использование принципов блочно-иерархического подхода к проектированию приводит к появлению, иерархии математических моделей проектируемых объектов. Количество иерархических уровней при моделировании определяется сложностью проектируемых объектов и возможностью средств проектирования. Однако для большинства предметных областей можно отнести имеющиеся иерархические уровни к одному из трех обобщенных уровней, называемых далее микро-, макро- и метауровнями. В зависимости от места в иерархии описаний математические модели делятся на ММ, относящиеся к микро- , макро- и метауровням.

Особенностью ММ на микроуровне является отражение физических процессов, протекающих в непрерывных пространстве и времени. Типичные ММ на микроуровне - дифференциальные уравнения в частных производных (ДУЧП). В них независимыми переменными являются пространственные координаты и время. С помощью этих уровней рассчитываются поля механических напряжений и деформаций, электрических потенциалов, давлений, температур и т.п. Возможности применения ММ в виде ДУЧП ограничены отдельными деталями, попытки анализировать с их помощью процессы в многокомпонентных средах сборочных единицах, электронных схемах не могут быть успешными из-за чрезмерного роста затрат машинного времени и памяти.

На макроуровне используют укрепленную дискретизацию пространства по функциональному признаку, что приводит к представлению ММ на этом уровне в виде систем обыкновенных дифференциальных уровней (ОДУ). В этих уровнях независимой переменной является время t, а вектор зависимых переменных ) составляют фазовую переменную, характеризующие состояние укрупненны элементов дискретизированного пространства. Такими переменными являютс силы и скорости в механических системах. Системы ОДУ являютс универсальными моделями на макроуровне, пригодными для анализа ка динамических, так и установившихся состояний объекта. Модели дл установившихся режимов можно также представить в виде систе] алгебраических уравнений. Порядок системы уравнений зависит от числ выделенных элементов объекта. Если порядок системы приближается к 10- , т< оперирование моделью становится затруднительным и поэтому необходим* переходить к представлениям на метцуровне.

На метауровне в качестве элементов принимают достаточно сложны» совокупности деталей. Метауровень характеризуется большим разнообразие!* типов используемых ММ. Для многих объектов ММ на метоуровне по прежнем] представляются системами ОДУ. Однако так как в моделях не описываются внутренние для элементов фазовые переменные, а фигурируют только фазовые переменные, относящиеся к взаимным связям элементов, то укрупнение элементов на метоуровне означает получение ММ приемлемой размерности для существенно более сложных объектов, чем на макроуровне.

В ряде предметных областей удается использовать специфические особенности функционирования объектов для упрощения ММ. В результате ММ становится системой логических уравнений, описывающих процессы. Такие логические модели существенно более экономичнее. Важный класс ММ на метауровне составляют модели массового обслуживания, применяемые для описания процессов функционирования информационных и вычислительных систем, производственных участков, линий и цехов.

Структурные модели также делятся на модели различных иерархических уровней. При этом на низших и иерархических уровней преобладает использование геометрических моделей, на высших иерархических уровнях используются топологические модели.

По степени детализации описания в пределах каждого иерархического уровня выделяют полные ММ и макромодели. Полная модель в отличие от макромодели описывает не только процессы на внешних выводах объекта, но и внутренние для объекта процессы. Полная ММ - модель, в которой фигурируют фазовые переменные, характеризующие состояния всех имеющихся межэлементных связей (т.е. состояния всех элементов проектируемого объекта). Макромодель - ММ, в которой отображаются состояния значительно меньшего числа межэлементных связей, что соответствует описанию объекта при укрупненном выделении элементов. Понятие «полная ММ» и «макромодель» относительны и обычно используются для различения двух моделей, отображающих различную степень детальности описания свойств объекта.

По способу представления свойств объекта функциональные ММ делятся на аналитические и алгоритмические. В общем случае математические модели могут

быть символическими и численными. При использовании символических, моделей оперируют не значениями величин, а их символическими обозначениями (индификаторами). Численные модели могут быть аналитическими, т.е. их можно представить в идее явно выраженных зависимостей выходных параметров Y от параметров внутренних X и внешних Q , или алгоритмическими, в которых связь Y, Хи Q задана неявно в виде алгоритма моделирования.

Аналитические ММ представляют собой явные аналитические выражения выходных параметров как функций выходных и внутренних параметров, т.е. имеют вид (1.1). Такие ММ характеризуются высокой экономичностью, однако получение формы (1.1) удается лишь в отдельных частных случаях, как правило, при принятии существенных допущений и ограничений, снижающих точность и сужающих область адекватности модели.

Алгоритмические ММ выражают связи выходных параметров с параметрами внутренних и внешних в форме алгоритма. Важнейший частный случай алгоритмических моделей - имитационные, они отображают процессы в системе при наличии внешних воздействий на систему. Другими словами, имитационная модель - это алгометрическая поведенческая модель. Примерами имитационных ММ могут служить модели динамических объектов в виде систем ОДУ и модели систем массового обслуживания, заданные в алгоритмической форме. Обычно в имитационных моделях фигурируют фазовые переменные. Так, на макроуровне имитационные модели представляют собой системы алгебро-диффиренциальных уравнений

где V - вектор фазовых переменных; t - время; V₀- вектор начальных условий. К примерам фазовых переменных можно отнести точки и напряжения в электрических системах, силы и скорости - в механических, давления и расходы - в гидравлических.

Для получения ММ используют методы неформальные и формальные. Неформальные методы применяют на различных иерархических уровнях для получения ММ элементов. Эти методы включают изучение закономерностей процессов и явлений, связанных с моделируемым объектом, выделение существенных факторов, принятие различного рода допущений и их обоснование, математическую интерпретацию имеющихся сведений и т. п. Для выполнения этих операций в общем случае отсутствуют формальные методы, в то же время от результата этих операций существенно зависят показатели эффективности ММ - степень универсальности, точность экономичность. Потому построение ММ элементов, как правило, осуществляется квалифицированными специалистами, получившими подготовку, как в соответствующей предметной области, так и вопросах математического моделирования на ЭВМ.

Применение неформальных методов возможно для синтеза ММ теоретических и эмпирических. Теоретические ММ создаются в результате исследования процессов и их закономерностей, присущих рассматриваемому классу объектов и

явлений; эмпирические ММ - в результате изучения внешних проявлений свойств объекта с помощью измерений фазовых переменных на внешних входах и выходах и обработки результатов измерений.

Решение задач моделирования элементов облегчается благодаря тому, что для построения большинства технических объектов используются типовые элементы (количество типов сравнительно не велико). Поэтому разработка ММ элементов производится сравнительно редко. Единожды созданные ММ элементов в дальнейшем многократно применяют при разработке разнообразных системах из этих элементов. Примерами таких ММ на микроуровне служат описания конечных элементов для анализа напряженно-деформированного состояния деталей (стержни, плоские элементы в виде треугольников и четырехугольников, трехмерные элементы типа параллелепипеда, тетраэдра и т. д); примерами ММ геометрических элементов этого уровня могут служить уравнения линий прямых, дуг окружностей, плоскостей и поверхностей второго порядка. Формальные методы применяют для получения ММ систем при известных математических моделях элементов. Таким образом, получение ММ проектируемых объектов обеспечивается реализацией ММ элементов и методов формирования ММ систем.

Кроме того, известны понятия статических и динамических, детерминированных и стохастических, аналоговые и дискретных. Статические модели описывают статическое состояние, в них не присутствует время в качестве независимой переменной. Динамические модели отражают поведение системы, т.е. в них обязательно используется время. Стохастические и детермированные модели различают в зависимости от учета или не учета СЛуЧНЙНЫХ фЗКТОрОВ. В аналоговых моделях фазовые переменные — непрерывные величины, в дискретных - дискретные, в частном случае дискретные модели являются логическими (булевыми), в них состояние системы и ее элементов описывается булевыми величинами. В ряде случаев полезно применение СМешаННЫХ Моделей, В КОТОРЫХ ОДНа часть подсистем характеризуется аналоговыми моделями, другая - логическими.

Информационные модели относятся к информационной страте автоматизированных систем, их используют для описания связей между единицами информации и прежде всего при инфологическом проектировании баз данных.

Наибольшие трудности возникают при создании моделей слабоструктурированных систем, что характерно, прежде всего, для системного уровня проектирования. Здесь значительное внимание уделяется экспертным методам. В теории систем сформулированы общие рекомендации по подбору экспертов при разработке модели, организации экспертизы, по обработке полученных результатов. Достаточно общий подход к построению моделей сложных слабоструктурированных систем выражен в специальных методиках IDEF.

\

Методика получения математических моделей. В общем случае процедур получения математических моделей включает в себя следующие операции:

1. Выбор свойств объекта, которые подлежат отражению в модели. Это выбор основан на анализе возможных применений модели и определяет степей универсальности ММ.

2. Сбор исходной информации о выбранных свойствах объекта. Источникам] сведений могут быть опыт и знания инженера, разрабатывающего модель научно-техническая литература, прежде всего справочная, описания прототипов - имеющихся ММ для элементов, близких по свойствам к исследуемому результаты экспериментального измерения параметров и т. п.

3. Синтез структуры ММ. Структура ММ — общий вид математически? соотношений модели без конкретизации числовых значений фигурирующих i них параметров. Структура модели может быть представлена также е графической форме, например в виде схемы или графа. Синтез структуры — наиболее ответственная и сложно формализуемая операция.

4. Расчет числовых значений параметров ММ. Эта задача ставится как задача минимизации погрешности модели заданной структуры

где X- вектор параметров модели; ХД - область варьирования параметров; s_m определяется в соответствии с (2.1) и (2.2).

2. Оценка точности и адекватности ММ. Для оценки точности должны использоваться значения У, _Ист., которые не фигурировали в задаче (2.3).

Большую ценность для пользователя представляют не оценки погрешности

Е_т, выполненные В одной — двух случайных точках пространства внешних

переменных, а сведения об области адекватности однако, её определение в многомерном пространстве требует больших затрат машинного времени. Поэтому иногда применяют аппроксимацию области адекватности.

Преобразования математических моделей. Выше были определены классы функциональных ММ на различных иерархических уровнях как системы уравнений определенного типа. Реализация таких моделей на компьютере подразумевает выбор численного метода решения уравнений и преобразование уравнений в соответствии с особенностями выбранного метода. Конечная цель преобразований - получение рабочей программы анализа в виде последовательности элементарных действий (арифметических и логических операций), реализуемых командами вычислительного устройства. Все указанные преобразования исходной ММ в последовательность элементарных действий ВЫПОЛНЯЮТСЯ автоматически по программам, создаваемым инженером- разработчиком САПР. Инженер-пользователь САПР должен лишь указать, какие программы из имеющихся он хочет использовать. Процесс преобразований ММ, относящихся к различным иерархическим уровням, иллюстрирует рис. 2.3.

Инженер-пользователь задает исходную информацию об анализируемой объекте и о проектных процедурах, подлежащих выполнению, на удобном дл* него проблемно-ориентированном входном языке программного комплекса.

Рис. 2.3. Схема процесса преобразования ММ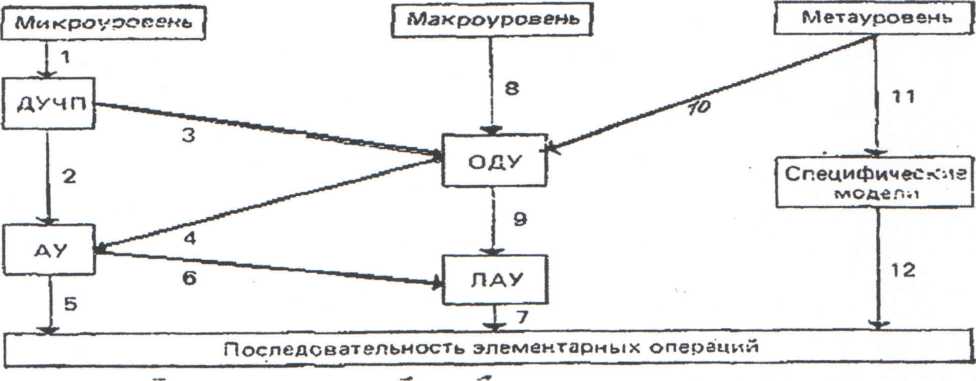

Ветви 1 на рис. 2.3 соответствует постановка задачи, относящейся к микроуровню, как краевой, чаще всего в виде ДУЧП. Численные методы решения ДУЧП основаны на дискретизации переменных и алгебраизации задачи. Дискретизация заключается в замене непрерывных переменных конечным множеством их значении в заданных для исследования пространственном и временном интервалах, алгебраизация - в замене производных алгебраическими соотношениями.

Применяют различные способы дискретизации и алгебраизации переменных при решении ДУЧП. Эти способы составляют сущность методов числового решения; большинство используемых методов относится либо к методам конечных разностей, либо к методам конечных элементов. Если ДУЧП стационарное (т. е. описывает статические состояния), то дискретизация и алгебраизация преобразует ДУЧП в систему алгебраических уравнений, в общем случае нелинейных (АУ) (ветвь 2 на рис.2.3). Если ДУЧП нестационарное (т. е. описывает изменяющиеся во времени и пространстве поля переменных), то дискретизацию и алгебраизацию можно представить состоящей из двух этапов: устранение производных по пространственным координатам (ветвь 3), результат

• система ОДУ; устранение производных по времени (ветвь 4).

Для численного решения ОДУ при заданных начальных условиях (задача Коши) разработано большое количество численных методов, причем многие из эффективных методов получили развитие под влиянием потребностей автоматизированного проектирования. Специфика алгебраизации производных по времени и обуславливает целесообразность выделения для ветви 4 специальных средств математического и программного обеспечения, отличных от таких же средств для ветвей 2 и 3.

b-Cbui

Г-

Сведение задачи решения алгебраических уравнений к последовательност] элементарных операций может быть либо непосредственным (ветвь 5), например, н; основе методов простых итераций или релаксаций, либо через посредств< предварительной линеаризации уравнений (ветвь 6), что составляет сущносп метода Ньютона. Решение системы линейных алгебраических уравнений (ЛАУ) i этом случае (ветвь 7) выполняется с помощью прямых методов, например метод? Г аусса.

Ветви 8 на рис. 2.3 соответствует постановке исходного описания задачи, относящегося к макроуровню в систему ОДУ с известными начальными условиями. Если это система нелинейных ОДУ, то дальнейшие преобразования происходят по охарактеризованным выше ветвям 4, 6, 7 или 4, 5; если же система линейных ОДУ, то целесообразен непосредственный переход к системе линейных алгебраических уравнений (ветвь 9).

Для анализа объектов на метауровне применяют либо переход к системе ОДУ (ветвь 10), либо переход к системам логических уравнений, моделям массового обслуживания их аналитическим моделям, отображающим упрощенно технико­экономические показатели объекта (ветвь 11). Сведение этих форм моделей в последовательность элементарных вычислительных операций (ветвь 12) не вызывает затруднений.

Сказанное показывает важное значение, отводимое в математическом обеспечении САПР численным методам решения систем ОДУ, нелинейных и линейных алгебраических уравнений. Из рис. 2.3 также видно, что такие системы уравнений приходится решать при проектировании объектов на микро и макроуровнях, а часто и на метауровне. От эффективности этих методов существенно зависит общая эффективность выполнения проектных процедур функционального проектирования.

Численные методы решения задач моделирования. Большинство задач анализа (моделирования) в САПР сводится к решению систем уравнений алгебраических или обыкновенных дифференциальных.

Для решения систем нелинейных алгебраических уравнений применяют итерационные методы. Главными показателями эффективности этих методов являются вероятность и скорость сходимости итераций к корню системы.

Наибольшей скоростью сходимости обладает метод Ньютона, основанный на линеаризации исходной системы уравнений и вычислении нового приближения к корню путем решения линеаризованной системы. Однако этот метод имеет ограниченную область сходимости - итерации сходятся, если начальное приближение было выбрано в достаточно малой окрестности корня. Однако заранее не известны ни положения корня, ни размеры области сходимости.—^

_ Поэтому в САПР находят применение также итерационные методы, для которых имеются сравнительно простые способы обеспечения сходимости, что приводит к значительным затратам машинного времени. Основными представителями этих методов являются релаксационные методы.

Среди других методов решения систем нелинейных уравнений в САПР находят применение: метод установления, заключающийся в сведении задачи к=еищше.

к решению системы ОДУ методами численного интегрирования; метод Продолжения решения по параметру, заключающийся в многократном решении задачи, например методом Ньютона при управлении продолжением области сходимости с помощью некоторого параметра; методы оптимизации, заключающиеся в минимизации нормы вектора навязок, так как очевидно, что в точке корня эта норма минимальна и равна нулю.

Основным методом решения нелинейных алгебраических уравнений в САПР следует считать метод Ньютона, используемый в рамках метода установления или метода продолжения решения по параметру.

Для решения систем линейных алгебраических уравнений в различных процедурах автоматизированного проектирования в основном используется метод Гаусса, заключающийся в последовательном исключении неизвестных исходной системы. В задачах автоматизированного проектирования характеризующихся большой размерностью, метод Гаусса следует применять при учёте свойства разреженности матриц коэффициентов, иначе затраты машинных времени и памяти могут оказаться чрезмерно большими. В первую очередь это относится к системам уравнений, получаемым в результате дискретизации и алгебратизации дифференциальных уравнений в частных производных, поскольку порядок системы алгебраических уравнений здесь может достигать значений 10^J и выше.

Численное интегрирование систем ОДУ возможно как явными, так и неявными методами. Большинство методов интегрирования является ограниченно устойчивым. Это означает, что на величину шага интегрирования накладываются ограничения, несоблюдение которых ведет к резкому искажению числовых результатов, колебанию числового решения вокруг истинного с нарастающей амплитудой, что обычно приводит к переполнению разрядной сетки ЭВМ и прекращению вычислений.

Явные методы наиболее легко реализуются, приводят к сравнительно небольшому объему вычисления на одном шаге интегрирования. Однако для соблюдения условий устойчивости приходится уменьшать шаг настолько, что увеличившееся число шагов может сделать недопустимо большими общие затраты машинного времени. Поэтому явные методы, к которым относятся известные методы Адамса-Башфорта и явные варианты метода Рунге-Кутта, оказываются малонадёжными и в САПР находят ограниченное положение.

Основными методами численного интегрирования систем ОДУ в САПР стали неявные методы. Среди них имеются методы, обеспечивающие устойчивость вычислений при любом шаге. Это неявные методы первого и второго порядка точности. В САПР рекомендуется применять неявные методы второго порядка точности или методы с автоматически меняющимся порядком, так как именно эти методы обеспечивают наилучшее удовлетворение противоречивых требований к точности и быстроту вычислений.

Требования к методам и алгоритмам анализа. При выборе или разработке метода (алгоритма) анализа прежде всего устанавливается область его применения. Чем шире круг задач и ММ, которые объявлены как допустимые для решения данным методом, тем этот метод универсальнее.

В большинстве случаев четкая и однозначная формулировка ограничений на применение метода затруднительна. Возможны ситуации, когда оговоренные заранее условия применения метода выполняются, однако удовлетворительное решение задачи не получается. Следовательно, вероятность успешного применения метода в оговоренном заранее классе задач меньше единицы. Эта вероятность является количественной оценкой важного свойства методов и алгоритмов - надежности.

Отказы в решении задач могут проявляться в несходимости итерационного процесса, в превышении погрешностями предельно допустимых значений и т.д. Причинами отказов могут быть такие факторы, как плохая обусловленность ММ, огранич^^ с?ад1ШООТд..Рданщшн^ сходимость. Так, итерации по

методу Ньютона при 'решении систем нелинейных алгебраических уравнений сходятся только в случае выбора начального приближения в достаточно малой окрестности корня. В САПР должны применяться надежные методы и алгоритмы. Для повышения надёжности часто применяют комбинирование различных методов, автоматическую параметрическую настройку методов и т.д.

К методам и алгоритмам анализа, как и к ММ, представляют требования точности и экономичности. Точность характеризуется степенью совпадения точного решения уравнений заданной модели и приближенного решении, полученного с помощью оцениваемого метода, а экономичность - затратами вычислительных ресурсов на реализацию метода (алгоритма).

Оценки точности и экономичности могут быть теоретическими и экспериментальными. Теоретические оценки погрешностей, трудоемкости требуемых вычислений и объемов участвующих в переработке массивов обычно выполняются при принятии ряда упрощающих предположений о характере используемых ММ. Примерами могут служить предположения о гладкости или линейности функциональных зависимостей, некоррелированности параметров и т.д. Несмотря на приближенность теоретических оценок, они представляют значительную ценность, так как обычно характеризуют эффективность применения исследуемого метода не к одной конкретной модели, а к некоторому классу моделей. Например, именно теоретические исследования позволяют установить, как зависят затраты машинного времени от размерности и обусловленности ММ при применении методов численного интегрирования систем ОДУ. Однако теоретические оценки удобны, для определения характера таких зависимостей, но числовые значения показателей эффективности для конкретных случаев могут быть весьма приближенными.

Поэтому находят применение также экспериментальные оценки, основанные на определении показателей эффективности на наборе специально составляемых задач, называемых тестовыми. Тестовые ММ должны отражать характерные особенности моделей того класса, объектов, которые являются типичными для рассматриваемой предметной области. Результаты тестирования используются ДЛЯ сравнительной оценки методов и алгоритмов при их выборе для реализации в программном обеспечении САПР.