6.2. Свойства скалярного произведения
1. Скалярное произведение обладает переместительным свойством: ab=ba
Решение:
5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а 0 b, то а b
.
6.3. Выражение скалярного произведения через координаты
Пусть заданы два вектора
Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:
т.е
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.
Пример 6.2.
Доказать, что диагонали четырехугольника, заданного координатами вершин А(-4;-4;4), В(-3;2;2),C(2; 5;1), D(3;-2;2), взаимно перпендикулярны.
Решение: Составим вектора АС и BD, лежащие на диагоналях данного четырехугольника. Имеем: АС = (6;9;-3) и BD = (6;-4;0). Найдем скалярное произведение этих векторов:
АС • BD = 36 - 36 - 0 = 0.
Отсюда следует, что ACBD. Диагонали четырехугольника ABCD взаимно перпендикулярны.
11
Векторным
произведением
векторов
и
называется
вектор
,
который определяется следующими
условиями:
1) Его модуль равен
где
-
угол между векторами
и
.
2) Вектор перпендикулярен к плоскости, определяемой перемножаемыми векторами и .
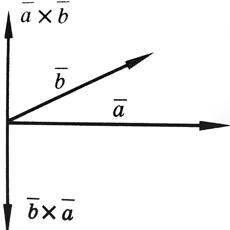
3) Вектор направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы и , кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать против часовой стрелки (см. рисунок).
Векторное
произведение векторов
и
обозначается
символом
:
(25)
или
(26)
Основные свойства векторного произведения:
1) Векторное произведение равно нулю, если векторы и коллинеарны или какой-либо из перемножаемых векторов является нулевым.
2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):
Векторное произведение не обладает свойством переместительности.
3)
(распределительное
свойство).
Выражение векторного произведения через проекции векторов и на координатные оси прямоугольной системы координат дается формулой
(27)
которую можно записать с помощью определителя
(28)
Проекции векторного произведения на оси прямоугольной системы координат вычисляются по формулам
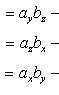
(29)
и тогда на основании (4)
(30)
Механический смысл
векторного произведения состоит в
следующем: если вектор
-
сила, а вектор
есть
радиус-вектор точки приложения силы,
имеющий свое начало в точке O,
то момент силы
относительно
точки O
есть
вектор, равный векторному произведению
радиуса-вектора
точки
приложения силы на силу
,
т. е.
Векторно-скалярное произведение трех векторов , и или смешанное их произведение вычисляется по формуле
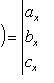
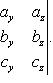(31)
Абсолютная величина векторно-скалярного произведения равна объему параллелепипеда, построенного на векторах , и . Объем пирамиды, построенной на векторах , и , получим по формуле
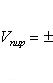
(32)
причем знак перед определителем должен быть выбран так, чтобы объем V был положительным (предполагается, что векторы , и не лежат в одной плоскости).
20. Три вектора , и называются компланарными, если они лежат в одной плоскости или параллельны одной и той же плоскости. Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю.
12