4. Управление, оптимальное по быстродействию, в разомкнутых системах.

4.1. Нахождение оптимальных управлений с помощью принципа максимума. Теорема об “n” интервалах.

Из всех методов нахождения оптимальных управлений для реше­ния задач о быстродействии наиболее целесообразно применять принцип максимума. Сформулируем задачу о быстродействии. В n-мерном фазовом пространстве в момент времени задан вектор состояния объекта ; дано его конечное значение в момент времени .

Объект управления описывается дифференциальным уравнением в векторной форме

. (4.1)

На управление накладывается ограничение . Задан функционал быстродействия.

. (4.2)

Требуется определить такой вектор , при котором время пе­рехода объекта из в минимально. Предполагается, что определены для любых значений , соответствующих области управления . Кроме этого, функции непрерывны по всем переменным и дифференцируемы по . Управление может принадлежать к классу кусочно-непрерывных функций, содержащих разрывы первого рода.

Решение задачи с помощью принципа максимума проводится по следующей схеме. Записывается функция Гамильтона Н [см. (3.25)], равная скалярному произведению векторов и

.

Берется частная производная от Н по и, которая определяет экст­ремум функции,

.

Эта производная зависит от одного или нескольких составляю­щих вектора . Функции меняются во времени. Для максимума H, как это требует принцип, необходимо, чтобы при и при , т. е. . Таким образом, требуется определить, сколько раз , меняет знак, или иначе говоря, сколько корней имеет функция.

У

Рис.4.1. Оптимальный ал­горитм	Рис.4.2. Соединение звеньев: а — последовательное, б, в — параллельное, г — нелинейный объект

правляющее воздействие скачком принимает значения или , или , как показано на рис. 4.1. При этом время перехода вектора состояния из начального состояния в конечное будет минимальным. Моменты смены знака управляющего воздействия называются моментами переключения. Характерные особенности строго оптимального процесса следующие: процесс должен происходить за конечное время; в момент окончания управления и после него координаты объекта должны иметь заданное значение.

Найдем оптимальные управления для трех структурных схем (рис. 4.2). Схема, представленная на рис. 4.2, а, достаточно известна и многократно описана в различных монографиях, а показанные на рис. 4.2, б, в, менее известны, поэтому остановимся на них подробнее. Схема, изображенная на рис. 4.2, б, применяется тогда, когда мощный поток материала или энергии по тем или иным причинам нельзя переработать в одном агрегате. Такие схемы особенно часто встречаются в химическом, обогатительном, металлургическом, цементном и т. д. производстве.

Схема, представленная на рис. 4.2, в, также нашла широкое при­менение в промышленности и на транспорте, например, в электрово­зах, у которых для привода колесных пар используется несколько двигателей, моменты которых суммируются; в технологических линиях бумажной и горной промышленности, где после переработки несколькими агрегатами готовые продукты поступают в смесители, отстойники и т. д.

Рассмотрим схему, показанную на рис. 4.2, а. Предположим, что каждое звено описывается линейным дифференциальным уравнением первого порядка с постоянными коэффициентами. В качестве фазовых координат выбираем . Тогда структурная схема описывается следующей системой уравнений в нормальной форме:

(4.3)

где

Составим функцию Гамильтона

(4.4)

Возьмем частную производную от Н по u

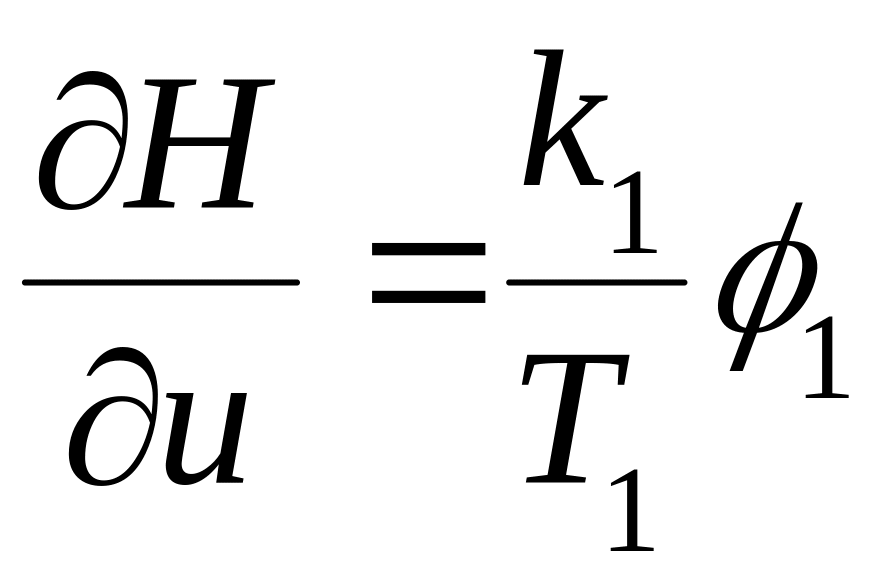(4.5)

и определим закон управления

Значит, требуется определить поведение функции . Для этого составляем уравнения для функций :

(4.6)

Решаем систему (4.6), начиная с последнего уравнения,

где - постоянная интегрирования, определяемая начальными условиями, для .

Отсюда

Продолжая решение, получим

(4.7)

Покажем, что функция имеет не более действитель­ных корней. Доказательство проведем методом математической индукции.

Обозначим число действительных корней функции через N. За базу индукции примем , N = 0. Это очевидно, так как функция при действительных корней не имеет. Предположим, что имеет N корней. Разделим функцию на знакопостоянный член е^t/Tn , что не изменит количества ее корней. В результате деления получим

(4.8)

Возьмем производную от

(4.9)

Выражение (4.9) содержит член, так как различные числа и их разности не равны нулю.

По известной теореме Ролля между двумя действительными корнями функции лежит, по крайней мере, один корень ее производной. Значит должна иметь (N—1) корней, так как по предположению имеет N корней. Но по базе индукции должна иметь (N—2) корней, так как она содержит член. Такое противоречие и является доказательством того, что функция имеет не более действительных корней.

Если вместо системы нормальных уравнений объект описывается одним дифференциальным уравнением n-го порядка и корни его характеристического уравнения отрицательные вещественные и различные, то решение для функций будет аналогично решению (4.7). Следовательно, если функция имеет (N —1) корней, то она меняет раз знак. Тогда для оптимального управления требуется п интервалов и знаки на интервалах чередуются раз.

Если среди корней характеристического уравнения имеются крат­ные или нулевые, то это не меняет количество интервалов управле­ния. Данное утверждение представляем доказать самим читателям.

Сформулируем теорему об «п» - интервалах, которая впервые была выдвинута и доказана А. А. Фельдбаумом. «Если объект управления описывается линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами и корни его характерис­тического уравнения вещественные отрицательные или нулевые, то для оптимального управления необходимо и достаточно п интервалов максимального значения управления , а знаки на интервалах должны чередоваться раз». Теорема об п интервалах значительно облегчает нахождение оптимальных управлений, так как она исключает необходимость определения функций и их анализа. Важно, чтобы были соблюдены условия теоремы, которые проверяются легко, когда объект описывается нормальной системой дифференциальных уравнений.

Перейдем к схеме, изображенной на рис. 4.2, б. Она описывается следующей системой уравнений:

(4.10)

где .

Составим функцию Гамильтона

(4.11)

Возьмем производную от Н по u

(4.12)

и определим закон управления

.

Таким образом, функция Н зависит от суммы всех составляющих вектора . Определим функции

(4.13)

Запишем решения для функций

Подставляем полученные выражения в (4.12)

(4.14)

Из предыдущего известно, что функция имеет (N—1) действительных корней. Таким образом, для оптимального управления необходимо n интервалов максимального значения управления ; при этом знаки на интервалах должны чередоваться (n - 1) раз. Если в структурной схеме содержатся звенья с одинаковыми динамическими свойствами, т. е. имеют одинаковые постоянные времени Т, то количество интервалов управления будет равно , где k — число звеньев с одинаковыми динамическими свойствами. При требуется всего один интервал управления. Справедливость последнего утверждения предлагается доказать читателям.

Рассмотрим схему, представленную на рис.4.2, в. Она описы­вается следующей системой уравнений:

(4.15)

где .

Начальное состояние объекта . Конечное состояние будет находиться на гиперплоскости, которая дается уравнением . Эта задача является задачей с подвижным правым концом, для которой требуется соблюдение условий трансверсальности.

Составим функцию Гамильтона

(4.16)

Найдем частную производную от Н по u

(4.17)

и определим функцию

Функции ; имеют такие же решения, как и в предыдущем случае; следовательно,

(4.18)

Постоянные интегрирования в (4.18) выбираем так, чтобы на конце управления соблюдались условия трансверсальности. Для этого вектор на конце управления должен быть параллелен вектору grad М, который имеет одно и то же значение в любой точке гиперплоскости. Найдем вектор градиента

(4.19)

В момент окончания управления, составляющие вектора должны быть равны составляющим градиента

(4.20)

Из (4.20) находим постоянные интегрирования

Все числа положительные. Подставим значения С_i, в (4.18), после чего получим

Функция знака не меняет, так как все члены при изменении возрастают, а остаются положительными. Значит, попасть за минимальное время на гиперплоскость можно с помощью только одного интервала управления при

На основе трех приведенных структурных схем могут быть рас­смотрены различные комбинации параллельно-последовательного соединения звеньев и получены для них оптимальные управления.

К данной задаче сводится случай, когда объект описывается урав­нением

(4.21)

Непосредственно применить принцип максимума к такому объек­ту нельзя, так как меняться скачком может не только высшая про­изводная. Этим нарушается основное условие принципа максимума о непрерывности изменения координат.

Уравнение (4.21) приводится к системе п уравнений в нормальной форме. Координаты, входящие в полученную таким образом систему уравнений, непрерывны, а поэтому правомерно использование принципа максимума. Каждой системе нормальных уравнений сопоставляется некоторая структурная схема. Легко показать, что нормальная система уравнений, соответствующая (4.21), представляется структурной схемой (рис. 4.2, в).

Рассмотрим оптимальное управление объектами, которые содер­жат нелинейные звенья (рис. 4.2, е). Объект, состоящий из линейного 1 и нелинейного звена 2, описывается следующей системой уравнений:

(4.22)

где

Функции и непрерывны вместе со своими про­изводными, причем и . Начальное состояние объекта , конечное состояние , .

Требуется за минимальное время перевести объект из начального состояния в конечное.

Запишем функцию Гамильтона

(4.23)

Возьмем частную производную от Н по u

(4.24)

и определим функцию

Для нахождения составляем уравнения сопряженных функций :

(4.25)

Решим уравнения (4.25):

(4.26)

Для определения алгоритма проанализируем поведение функций и . Функция знака не меняет, так как экспонен­циальный член всегда положителен. Таким образом, производная от функций знакопостоянна, а сама функция по теореме Ролля только один раз меняет знак. Значит, оптимальное управление должно иметь два интервала (разгон — торможение) с одной сменой знака. Данный пример показывает, что если в объекте управления имеются нелинейные звенья, то для нахождения оптимальных управлений необходимо исследовать свойства нелинейных функций, их производных и интегралов. В большинстве случаев эти исследования могут быть очень сложными. Без доказательства укажем, что если функции, описывающие нелинейные звенья, обладают ранее указанными свойствами, то все выводы, сделанные для схем (см. рис. 4.2), справедливы и для нелинейных звеньев. Так как свойства таких нелинейных объектов совпадают со свойствами линейных, то их можно назвать квазилинейными.

Выше были рассмотрены оптимальные управления для случая нулевых начальных и ненулевых конечных условий. Часто рассмат­риваются оптимальные управления по ошибке системы, т. е. по отклонению от конечного состояния. Тогда задача несколько изме­няется, так как начальные условия будут ненулевыми, а конечные - нулевыми. Для рассмотренных объектов такая трансформация не вызывает изменений в определении оптимальных алгоритмов.