3.6. Динамическое программирование.

Метод динамического программирования разработан американским математиком Р. Беллманом и его школой. Метод развивался в процессе решения вариационных задач на вычислительных машинах, поэтому содержит элементы дискретности. Постановка основной вариационной задачи в динамическом программировании такая же, как и в принципе максимума Понтрягина. При изложении используются материалы источников [8].

Рассмотрим пример решения вариационной задачи.

Пусть, между пунктами А и В (рис. 3.9) необходимо провести железную или шоссейную дорогу так, чтобы стоимость строительства была минимальной. Разобьём путь между А и В на горизонтальные и вертикальные участки. Обозначим стоимость строительства на каждом горизонтальном и вертикальном участке в некоторых условных е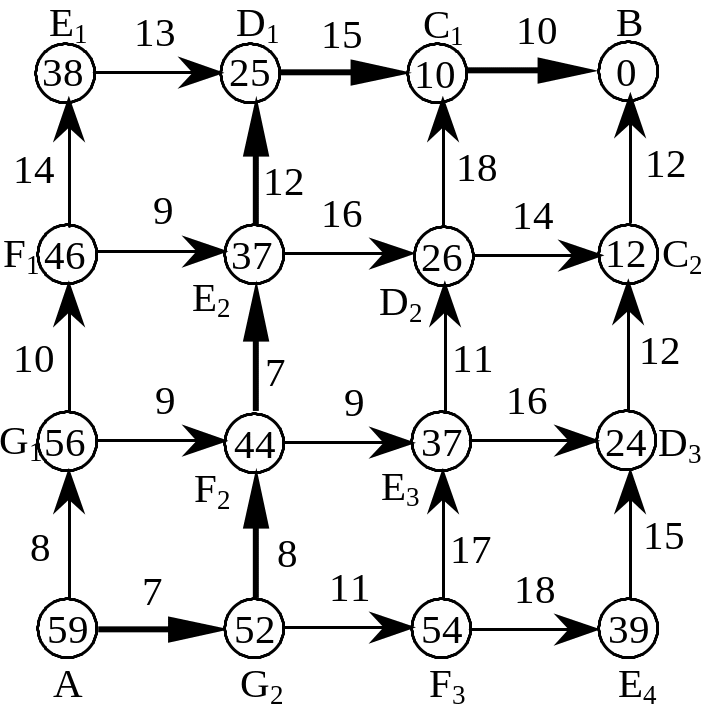 диницах (стоимость строительства можно заранее подсчитать по карте). Обозначим узловые точки , , , , . Начнём решение задачи с конечного пункта, за который примем точку В.

Рис. 3.9.

В точку В можно попасть за один (последний) шаг или из точки С₁ или из точки С₂. Предположим, что каким-либо способом удалось попасть в С₁ или С₂. Затраты на последний шаг будут 12 или 10 ед. Поставим величину затрат в кружки и укажем направление последнего шага стрелками. Сместимся теперь в точку D_i. Опять считаем, что каким то образом эти точки уже достигнуты. Проследим возможные пути в точку В. Из D₁ есть один путь через С₁, затраты при этом будут равны 25.

Из D₂ есть уже два пути: через С₁ и С₂. Один путь даёт затраты 28, а другой 26. Через С₁ в В путь менее рационален, поэтому его из дальнейших рассуждений исключаем. Ставим в D₂ кружок с затратами 26 и стрелку оптимального управления в сторону С₂. Также анализируем точку D₃. Из D₃ есть только один путь через С₂. Ставим в D₃ кружок с затратами 24 и стрелку оптимального управления в сторону С₂. Обратим внимание на то, что неоптимальная траектория сразу исключается из рассмотрения. В этом и состоит смысл динамического программирования. Перейдём к точке E_i. Точки Е₁ и Е₄ дают единственно возможные траектории.

Точки Е₂ и Е₃ дают по две траектории каждая, из которых выбираем оптимальные, т.е. дающие минимум затрат. Причём из точки Е_2­ используем только оптимальную траекторию. Из всех возможных путей из точек Е₁, Е₂, Е₃, Е₄ остаются только четыре (показаны стрелками). Переход таким же образом к точкам F_i, G_i и, наконец, к А, получаем оптимальный путь, который на рисунке отмечен жирной линией и даёт минимально возможный расход в условных единицах- 59. Оптимальный путь можно трактовать как оптимальную траекторию в принятой системе координат. Отметим ещё раз, что по мере продвижения от В к А последовательно исключились неоптимальные траектории. Это исключение значительно упростило нахождение оптимальной траектории. При простом переборе пришлось бы рассчитывать все траектории от А до В, которых всего 25. Заметим ещё особенность, которая заключается в том, что оптимальная траектория рассматривается не только на одном шаге, но и учитываются другие шаги. На каждом шаге траектория может быть и неоптимальной, но вся траектория в целом оптимальна. Сформулирован принцип оптимальности, который гласит, что любой отрезок оптимальной траектории также является оптимальным, а будущее поведение процесса не зависит от его предыстории, т.е. поведение системы в прошлом до начала управления.

Следует, однако, сделать оговорку. Для примера был взят очень простой случай. В реальных ситуациях даже разбиение на шаги и то представляет большие трудности, причём шагов может быть многие сотни. Поэтому идея метода динамического программирования в большинстве случаев реализуется сложным образом. Дадим математическую запись методу динамического программирования.

Пусть заданы динамические свойства объекта управления:

(3.30)

и начальные условия и . Выбираем критерий оптимальности:

(3.31)

где - функция управления, которая доставляет минимум функционалу J.

Обозначим через минимальное значение функционала, которое зависит от начальных условий и вида управления.

Допустим, имеется оптимальная траектория , которая обеспечивает минимальное значение интегралу J. Разобьем эту траекторию на два участка: первый от до , второй от до . Р. Беллманом был сформулирован принцип оптимальности, согласно которому будущее поведение системы, т.е. при , не зависит от «предыстории», т.е. поведение системы в прошлом, и определяется лишь её настоящее состоянием, т.е. в момент времени . Поэтому если траектория от до , оптимальная, то второй участок оптимальной траектории также является оптимальным. Кроме этого, второй участок может рассматриваться и как самостоятельная траектория с начальными условиями . Используя принцип оптимальности, представим интеграл J в виде:

(3.32)

.

Согласно принципу оптимальности Беллмана, если доставляет min интегралу

,

то она будет доставлять также min интегралу

.

Поэтому, учитывая (3.32) получим

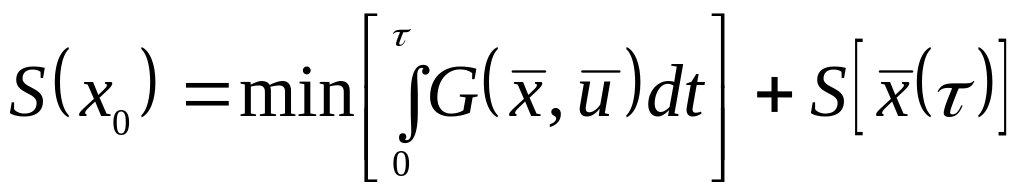
(3.33)

где - функция от начального состояния в момент .

Будем считать τ достаточно малой величиной.

Тогда

(3.34)

Применим к (3.34) формулу конечных приращений

(3.35)

Из (3.32) с учётом (3.35) можно записать

(3.36)

Вычтем из обеих частей последнего равенства

(3.37)

Для получения минимума по нужно продифференцировать (3.37) по .

(3.38)

Согласно принципу оптимальности начальные условия и можно заменить на текущие координаты и . Тогда получим окончательно функциональные уравнения Беллмана:

(3.39)

Выражения (3.39) представляют собой нелинейные дифференциальные уравнения в частных производных. Поэтому применение этого метода в некоторых случаях требует сложных расчётов и не всегда возможно в таком виде. Исключив из (3.39) , получим соотношение

(3.40)

Заметим здесь, что функция S должна быть дифференцируемой по х.