2.3. Задача ограничения энергетических ресурсов.
В подобных задачах требуется найти максимум функционала
,
если
т.е. постановка задачи аналогична, допустим, нахождение максимального угла поворота вала двигателя = J4 при ограничении количества тепла, которое выделяется в его якоре, Q =J5.
Все перечисленные задачи управления решаются с помощью:
классического вариационного исчисления;
принцип максимума Понтрягина;
динамического программирования Беллмона.
Классическое
вариационное исчисление целесообразно
применять к задачам, у которых области
изменения
и
открытые, т.е. не содержат ограничений.
Это справедливо в случаях, когда
рассматриваются малые
отклонения
и
от их установившихся значений.
Принцип
максимума Понтрягина применяется,
когда области
и
замкнутые, а координаты векторов
и
могут находиться на границах этих
областей.
3. Математические основы теории оптимальных систем.
3.1. Функционалы, вариации и их свойства.
Методы решения вариационных задач схожи с методами исследования функций на max и min.
Рассмотрим
некоторую функцию
.
Каждому значению аргумента t
соответствует число х. Допустим, х=е-t/T,
тогда каждому
соответствует числа
.
Теперь возьмём функционал:
Каждой функции х(t) будет соответствовать число J. Если х(t) = е-t/T ,тогда:
Каждому
набору функций е-t/T
будут соответствовать числа
.
Приращением (или вариацией) функции х(t) называется разность между двумя функциями х = x1(t) – x2(t). В данном примере вариация х может быть равна х = е-t/T1 - е-t/T2.
Функция х(t) непрерывна, если малому изменению t соответствует малое изменение х(t). Функционал непрерывен, если малому изменению х(t) соответствует малое изменение J.
Если
функционалы содержат производные, то
в этом случае понятие непрерывности
усложняется. Поэтому рассматривают не
только разности самих функций, но и их
производных, т.е.
.
Считается, что функционал непрерывен, если малому изменению функции и её производных соответствует малое приращение функционала.
3.2. Понятие линейности функционала.
Линейными функционалами называются такие, для которых справедливы следующие условия:
;
.
Если приращение функции х(t) представляется в виде
то и приращение функционала получается аналогично
Линейная часть приращения функционала по отношению к х называется вариацией функционала и обозначается J. Вариация функционала аналогична дифференциалу функции dx. Известно, что если некоторая функция в точке t0 имеет экстремум, то dx=0. Так как вариация аналогична дифференциалу, то для того, чтобы функционал имел экстремум, его вариация должна равняться нулю, т.е. J=0. Таким образом, если имеются несколько функций, и одна из них доставляет экстремум функционалу, то эту функцию и нужно выбирать в качестве решения задачи. Функции, на которых вариация функционала J=0, называются экстремалями.
3.3. Уравнение Эйлера. Уравнение Эйлера-Пуассона. Условия трансверсальности.
В
.
Было установлено, что для некоторых функций функционалы принимают экстремальные значения. Как же среди множества функций найти те, которые дают экстремум функционалу? Ответ на этот вопрос даёт уравнение Эйлера, решение которого является экстремалью. Приведём упрощённый вывод уравнения Эйлера. Пусть задан функционал вида
(3.1)
Требуется найти функцию, которая даёт минимум функционалу (3.1). Геометрически эта задача трактуется на рис. 3.1. Даны две точки х(t0) и х(t1). Нужно найти уравнение такой линии 1, которое при подстановке в функционал J. Давало бы ему экстремум.
Предположим, что такая линия найдена, т.е. найдена функция, её описывающая. Проварьируем эту функцию и определим приращение функционала.
(3.2)
Рис 3.1.
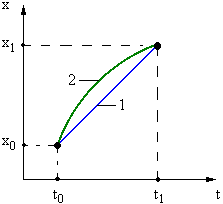
Вариацию аргумента выберем таким образом, чтобы δх(t0)=0 и δх(t1)=0, т.е. варьируемая линия 2 должна проходить через точку х(t0)=х0 и х(t1)=х1.
Разложим проварьированную функцию вряд Тейлора.
(3.3)
где Rn- остаток порядка малости больше двух.
Первый член разложения (3.3) в фигурных скобках называется первой вариацией, она линейна. Второй член называется второй вариацией, она нелинейная. Ранее было условленно, что рассматривается только линейная часть приращения функционала, т.е. первая вариация, а поэтому всеми высшими вариациями можно пренебречь.
Учитывая это, получим выражение для вариации функционала.
(3.4)
Проинтегрируем по частям второе слагаемое в (3.4)
(3.5)
Первое слагаемое в (3.5) равно нулю, т.к. х(t0) =х(t1)=0 по условию задачи. Тогда вариация будет равна
(3.6)
так как согласно свойствам функционалов, чтобы J имел экстремум, его вариация J должна быть равна нулю. По лемме Лагранжа интеграл (3.6) равен нулю тогда, когда подынтегральная функция равна нулю, т.е.
(3.7)
Уравнение (3.7) называется уравнением Эйлера. Среди решений этого уравнения следует искать экстремами. Чтобы установить, действительно ли имеет место экстремаль, часто прибегают к рассмотрению физической картины явления.
Покажем методику использования уравнения Эйлера. Требуется определить, какое уравнение соответствует минимуму функционала
Находим производные, входящие в уравнение Эйлера.
Получим уравнение Эйлера:
или
.
Решение уравнения:
.
Если
рассматривать некоторый затухающий
процесс, то при
.
Это возможно тогда, когда
.
Постоянную
найдём из начальных (граничных) условий
при
.
Отсюда
.
Поэтому окончательно получим решение
вида:
.
Это уравнение экстремали. Однако,
нетрудно заметить, что экстремаль
соответствует решению однородного
дифференциального уравнения вида:
т.о. для затухающих процессов решение уравнения Эйлера (экстремаль) соответствует общему решению однородного линейного дифференциального уравнения с постоянными коэффициентами.
М
Рис. 3.2.
Итак, мы переходим к простейшей задаче вариационного исчисления.
Теорема.
Для того, чтобы функционал (3.1), определённый
на множестве функций
,
имеющих непрерывную первую производную
и удовлетворяющих граничным условиям
(3.8)
достигал
на данной функции
экстремума, необходимо, чтобы эта
функция удовлетворяла уравнению Эйлера:
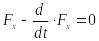
Интегральные кривые уравнения Эйлера называются экстремалями (лагранжевыми кривыми). При этом экстремум функционала (3.1) может реализовываться только на тех экстремалях, которые удовлетворяют уравнениям (3.8).
Надо иметь в виду, что кривая задача
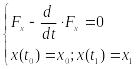
(3.9)
не всегда имеет решение, а если решение существует, то оно может быть не единственным.
Мы рассмотрели случай, когда в функционале (3.1) входила только первая производная, однако (в общем случае) в функционал могут входить и производные высших порядков.
Проводя для таких функционалов аналогичные рассуждения, придём к уравнению Эйлера – Пуассона.
(3.10)
Сложнее обстоит дело, когда граничные точки не закреплены, а могут находиться на некоторых поверхностях или линиях. Уравнение Эйлера в этом случае дополняется условиями трансверсальности. Смысл их заключается в следующем. Когда рассматривалось уравнение Эйлера, то граничные точки были заданы. Такая задача называется задачей с закреплёнными концами. Из граничных условий находились постоянные интегрирования, и тем самым получалось конкретное решение уравнения Эйлера. Если же экстремаль должна проходить между поверхностями или линиями, то никаких определённых граничных точек не задаётся. Они могут находиться в любой точке поверхности или линии. Поэтому для определения постоянных интегрирования нужно иметь некоторые условия. Поясним с помощью построений, изображённых на рис. 3.3, геометрический смысл этих условий.
П
Рис. 3.3
и
.
Требуется найти экстремаль, которая
соединила бы их по кратчайшему пути.
Экстремаль может начинаться в любой
точке на
и оканчиваться в любой точке на
.
Точки эти находятся из следующих соотношений, которые называются условиями трансверсальности:
(3.11)
Условия трансверсальности дают возможность определить постоянные интегрирования в уравнении Эйлера и тем самым получить конкретное решение.
Часто условия трансверсальности сводятся к условиям ортогональности, т.е. экстремаль и заданные линии или поверхности должны пересекаться под прямым углом.