5. Управление, близкое к оптимальному.

Рассмотренные выше системы оптимальны только в идеальных случаях. Реальные системы всегда будут системами, близкими к оптимальным. Это объясняется многими причинами. Так, например, реализовать моменты переключения нельзя с большой точностью, так как современные реле имеют зону нечувствительности, гистерезис, конечное время срабатывания, т.е. не идеальные релейные характеристики, необходимые для оптимального управления. Звенья с насыщением, которые используются в качестве релейных элементов, имеют зоны линейности и их нужно учитывать при приближении к конечной цели управления. При малых входных сигналах такие оптимальные системы работают, как обыкновенные замкнутые линейные системы. Значительные упрощения и идеализация допускаются и при математическом описании объектов. Имеющиеся средства контроля фазовых координат также имеют определенные погрешности измерения, из-за которых не удается получить оптимальное управление. Кроме того, часто реализация оптимальной системы бывает настолько сложна, что ее изготовление и эксплуатация экономически невыгодны. Поэтому можно сразу спроектировать не оптимальную систему, а систему, близкую к оптимальной. Как правило, это приводит к упрощению системы за счет снижения ее качества. Но в большинстве случаев выигрыш от упрощения значительно превосходит проигрыш от ухудшения качества.

Если теория оптимальных процессов, как это было видно, доста­точно разработана, то вопросом реализации систем, близких к опти­мальным, уделяется меньшее внимание, несмотря на их перспектив­ность.

5.1. Уменьшение количества интервалов управления.

Сокращение количества интервалов управления возможно в двух случаях. Первый случай предусматривает понижение порядка дифференциального уравнения. Действительно, любой объект или систему можно разбить на апериодические или интегрирующие звенья. Апериодические звенья будут иметь разные постоянные времени. Часто бывает, что некоторые из постоянных времени значительно меньше остальных. Значит в звеньях, которые имеют малые постоянные времени, будет запасаться относительно малое количество энергии или вещества. Эти малые количества будут незначительно сказываться на векторе состояния , а поэтому ими можно пренебречь. Правда, нет четких критериев, которые позволили бы определенно решить, какими постоянными времени можно пренебречь. По аналогии с теорией регулирования рекомендуется пренебрегать теми постоянными времени, которые в 10 раз и более меньше остальных. Если объект нельзя разбить на звенья, то следует найти корни характеристического уравнения, соответствующего дифференциальному уравнению. Некоторые корни могут быть более чем в 10 раз больше остальных, поэтому ими пренебрегают. Большим корням соответствуют быстро затухающие переходные процессы, которые оказывают незначительное влияние на вектор состояния . Таким образом, пренебрегая некоторыми постоянными времени, понижают порядок дифференциального уравнения, т.е. описывают объект, допустим, не уравнением третьего порядка, а уравнением второго порядка. Этим самым сокращается количество интервалов с трех до двух, а это уже значительно упрощает реализацию алгоритма.

Второй случай связан с пренебрежением отдельными интервалами. Встречаются такие соотношения параметров объекта, граничных условий и вектора управления, что, наряду с достаточно большими интервалами, некоторые интервалы становятся очень малыми, до­пустим, десятые и сотые доли секунд. Если такие интервалы нельзя реализовать с помощью имеющейся аппаратуры, то ими приходится пренебрегать. Ошибка при этом получается достаточно малой, так как за малый промежуток времени вектор состояния не может сильно измениться. Кроме того, можно сознательно пренебречь некоторыми интервалами управления, обычно последними, которые, как правило, значительно меньше первых, но так, чтобы цель управления достигалась с заданной точностью. Иными словами, вектор состояния должен попасть не в точку, а в заданную область фазового пространства. На конкретном примере покажем методику определения моментов переключения для управления, близкого к оптимальному.

Рассмотрим объект, который описывается дифференциальным уравнением второго порядка:

(5.1)

Для оптимального управления необходимо иметь два интервала управления и одну смену знака. Зададимся целью управлять объектом с помощью одного интервала. При таком управлении может возникать нежелательное отклонение вектора . Значит, переключение управляющего воздействия следует делать так, чтобы отклонения вектора не превосходили допустимых границ. Зададим эту границу в виде ошибки .

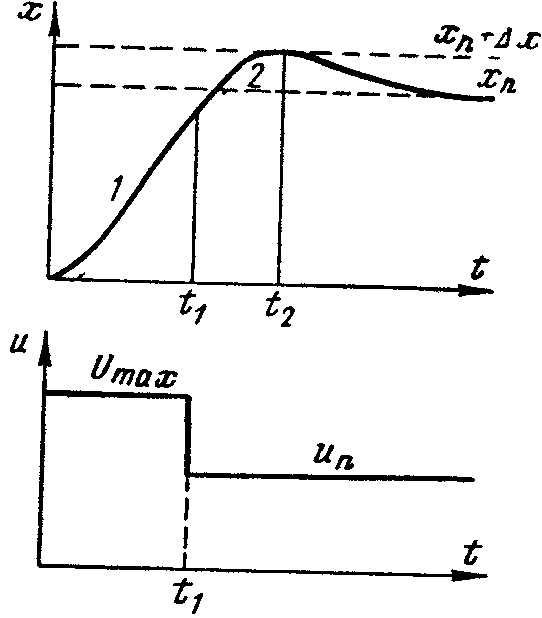
Для определения моментов переключения за конечное состояние объекта примем значение координаты . При этом значении координаты (рис.5.1).

Воспользуемся методом исключения постоянных интегрирования. Допустим, что известно время , за которое координата достигнет максимального значения, и время момента переключения .

Запишем следующие решения. Для участка 2 (см. рис. ) и точки максимума при .

(5.2)

,

где

Рис.5.1. Управление близкое

к оптимальному, приуменьшении

числа интервалов.

Здесь - максимальное значение координаты при ;

- входное управляющее воздействие, соответствующее номинальному значению выходной координаты.

Для начала движения при

(5.3)

где

В момент переключения при

;

(5.4)

.

Имея шесть уравнений и шесть неизвестных, решаем полученные системы относительно и . Из уравнений системы (5.4) определяем , а из (5.2) и (5.3) - , , , . После подстановки получим уравнения относительно и

(5.4)

Осталось два трансцендентных уравнения с двумя неизвестными и . Уравнения (5.5) решаются численным методом. Будем за­даваться, допустим, временем и определять из уравнений (5.5) время . Далее построим две функции , со­ответствующие двум уравнениям. Точка пересечения этих функций даст значения и . Существенным, конечно, является время .

Таким образом, задача определения момента переключения в зависимости от перерегулирования решена.

Процесс, показанный на рис.5.1, не является оптимальным, так как теоретически он заканчивается за бесконечное время. Но практически его можно назвать близким к оптимальному, так как в заданную область вектор попадает за конечное и минимальное время.

Если для объектов, которые описываются уравнением (5.1), мож­но найти момент переключения для одного интервала, то для объек­тов, которые описываются дифференциальными уравнениями более высоких порядков, это сделать не так престо. Объясняется это тем, что в процессах, близких к оптимальным, при одном интервале уп­равления известно значение только координаты и ее про­изводной . Высшие же производные неизвестны и поэтому системы уравнений, из которых исключаются постоянные интегриро­вания, неразрешимы. Для определения длительности одного интер­вала управления при высоком порядке дифференциального уравне­ния, описывающего объект, приходится проводить несколько раз расчеты переходных процессов и из них выбирать тот, который отвечает заданной ошибке .

Рассмотрим объект, который описывается дифференциальным уравнением:

(5.6)

Рис. 5.2. Управление, близкое к оптимальному, при уменьшении величины и

Для оптимального управления требуется два интервала и одна смена знака. Зададимся целью управлять объектом одним интервалом. Тогда при отключении управляющего воздействия возникнет свободное дви­жение, в результате которого вектор , вообще говоря, не попадет в задан­ную область. Но если как-то снизить запас энергии или вещества перед отключением, то можно достигнуть за­данной области. Запас энергии или вещества снижается уменьшением управляющего воздействия. Следова­тельно, надо выявить зависимость между допустимой областью и управляющим воздействием, при отключении которого вектор не выйдет за эту область. Зададим эту область в виде (рис. 5.2), т.е. допустимого отклонения самой координаты. Скорость х и сама координата связаны зависимостью х = хТ. Отсюда, если задано , получаем значение скорости

(5.7)

Таким образом, скорость следует снизить до значения за счет уменьшения управляющего воздействия до величины

(5.8)

Так как система инерционна, то после снижения управляющего воздействия с скорость, изменяясь по экспоненте

(5.9)

примет значение за бесконечно большое время.

Принято считать, что процесс заканчивается за 3Т. Тогда время, за которое скорость снизится от значения до будет =3T. Проинтегрировав выражение (5.9), получим изменение за время

Вид алгоритма управления и переходного процесса x(t) показан на рис. 5.2. Алгоритм управления значительно проще оптимального, так как не требуется реверсировать объект управления. Для электрических двигателей предварительное снижение скорости осуществляется включением добавочных сопротивлений.

Полученный алгоритм широко применяется для управления транспортными механизмами (шахтными подъемными машинами, вагоно-весами и т. д.). Таким образом, показана возможность умень­шения количества интервалов, однако с проигрышем качества опти­мального управления.

Идею уменьшения интервалов управления можно использовать и для синтеза оптимального автомата. Если уменьшается количество интервалов управления, то уменьшается и число переходов функции переключения через нуль. Этим достигается сокращение количества обратных связей. Определить количество интервалов управления, обеспечивающих необходимую точность, можно методами, рассмотренными выше. А, зная количество интервалов, обычным методом синтезируют оптимальный автомат.

Некоторые трудности вызывает выбор контролируемых коорди­нат вектора . Но, учитывая сложность замера высших производных, в качестве контролируемых составляющих вектора выбирают саму координату, ее первую и, редко, вторую производные. Синте­зированный таким образом автомат является автоматом, близким к оптимальному.