4.6. Определение знака первого интервала.

Во всех рассмотренных примерах первый интервал произвольно выбирался положительным. Очевидно, что знак первого интервала надо выбирать, исходя из начальных и конечных условий. Если начальные условия нулевые, то знак первого интервала определяется знаком заданной координаты. Иначе говоря, если задана координата , то управление следует начинать с положительного интервала, если задана координата , то с отрицательного интервала. При ненулевых начальных условиях знак первого интервала выбирается из следующих соотношений:

при первый интервал положительный;

при первый интервал отрицательный.

Данные соотношения справедливы только при равенстве нулю всех производных в начальный и конечный моменты управления, т. е. тогда, когда начальная и конечная точки фазовых траекторий лежат на оси х или на линии установившихся состояний.

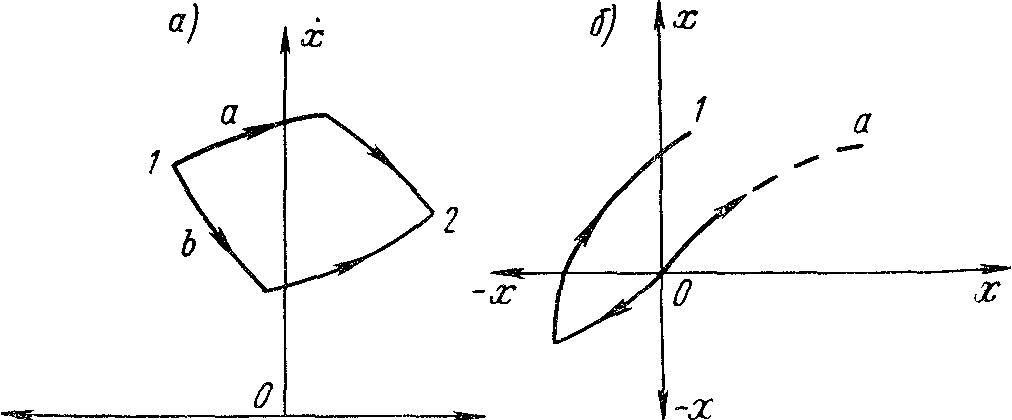
Рис.4.18. Определение знака первого интервала

Несколько сложнее определить знак первого интервала, когда начальные и конечные точки фазовых траекторий лежат в фазовом пространстве. На рис.4.18, а показана фазовая плоскость, где даны две точки: начальная 1 и конечная 2. Из точки 1 в точку 2 можно попасть по двум траекториям - a или b. Для движения по траектории а управление следует начинать с положительного интервала, а по траектории b - с отрицательного. Однако чем выше лежит фазовая траектория, тем быстрее протекает процесс. Поэтому время движения по траектории а будет меньшим, чем по траектории b. Естественно, что процесс, характеризующийся траекторией а, будет оптимальным. В данном простом случае легко определить знак первого интервала. В более сложных случаях, когда трудно изобразить фазовые траектории, приходится рассчитывать алгоритмы оптимального управления для положительного и отрицательного первого интервала. Алгоритм управления, дающий меньшее время, и будет оптимальным.

Рассмотрим еще случай, показанный на рис.4.18, б. По фазовой траектории а, соответствующей максимально допустимому поло­жительному управляющему воздействию, попасть в точку 1 из начала координат нельзя. Однако если сдвинуть фазовую траекторию влево первым отрицательным интервалом, то можно достичь точки 1. При затруднениях в получении фазовых траекторий нужно проделать расчет для двух алгоритмов управления: с положительным и отрицатель­ным первым интервалом.

В примере (см. рис.4.18, б) функция оптимального управления для первого положительного интервала вообще не имеет решения, т. е. не существует алгоритма управления, начинающегося с положительного интервала при данном ограничении и данных граничных условиях. Следовательно, необходимость выбора знака первого интервала в некоторых случаях может усложнить получение оптимального алгоритма управления.

При рассмотрении оптимальных систем были использованы простые примеры, в которых порядок дифференциальных уравнений не превышал двух. Естественно, что трудоемкость расчетов с повы­шением порядка дифференциальных уравнений сильно возрастает. В таких случаях желательно применять цифровую вычислительную машину. С ее помощью можно решать системы трансцендентных уравнений, определяющих функцию оптимального управления. Для расчетов оптимальных управлений были предложены блок-схемы вычислений на цифровой машине, одна из которых показана на рис. 4.19. Заметим, что вводить данные в ЦВМ нужно в цифровой форме; при этом результаты вычислений получаются также в цифровой форме. Для непосредственного управления это не совсем удобно, так как требует преобразования непрерывных величин в цифровые и наоборот.

Рассмотренные вопросы оптимального управления предполагали реализацию алгоритмов разомкнутыми системами. В таких системах не контролируется вектор состояния и предполагается, что он точно соответствует ожидаемому результату. Такие системы могут применяться только в идеальных случаях, т. е. когда отсутствует вектор возмущающих воздействий , не меняются коэффициенты дифференциальных уравнений и структура объекта управления. В реальных системах трудно соблюсти все эти условия, а, следовательно, и осуществить оптимальное управление в разомкнутой системе.

При жестком алгоритме управления, т.е. при постоянных мо­ментах переключения и действии возмущающих факторов, объект будет попадать в заданную точку фазового пространства с избытком или недостатком внутренней энергии. Это приведет к тому, что после управления вектор состояния сможет совершать свободные движения, удаляясь при этом от заданной точки. Если величина отклонений вектора от заданной точки укладывается в заданную точность при действии возмущающих факторов, то применить для оптимального управления разомкнутую систему возможно. Однако для этого следует проанализировать все возможные возмущающие факторы и ошибки, которые они могут вызвать. Так как многие возмущающие факторы, т.е. составляющие вектора , часто не известны, то и провести такой анализ нельзя. Реализация алгоритмов управления в разомкнутых системах не так проста, как это кажется на первый взгляд. Особенно она усложняется для реверсивных объектов и объектов, которые требуют изменения моментов переключения.

Синтез оптимальных алгоритмов и анализ изменения координат по изложенной методике лучше всего проводить на стадии проекти­рования, выбирая, допустим, наиболее целесообразный агрегат или технологическую схему. Очень полезно проделать расчеты оп­тимального управления для выяснения возможностей объекта уп­равления, даже если он и не автоматизируется.

Учитывая недостатки, которые присущи разомкнутым оптималь­ным системам, их можно рекомендовать только в сугубо специаль­ных случаях, допустим тогда, когда нельзя получить информацию вектора состояния .

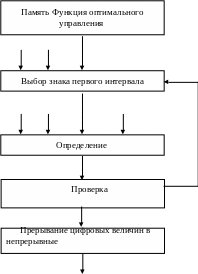
Рис.4.19. Блок-схема определения моментов переключения с помощью цифровой вычислительной машины.