Вопрос 18.
Парабола. Определение, основные свойства, уравнение и построение.
Парабола – геометрическое место точек, каждая из которых одинаково удалена от данной точки называемой фокусом параболы и данной прямой называемой директрисой.
Расстояние
от фокуса
до директрисы называется параметром
параболы и обозначается ρ(ρ>0)/
Выберем систему координат хОу, так чтобы оси Ох проходила через фокус перпендикулярен директрисе направлении от директрисы до фокуса. Начало координат О расположен между фокусом.
Тогда
фокус
будет
иметь координаты
,
а директриса задаваться уравнением х
Пусть
M(x;y)
произвольная точка параболы, а MN⍊к
директрисе,
=
;
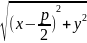N=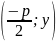
;
=
=
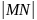По определению
=
=>
-
/2
=
=
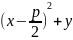=2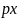
- каноническое уравнение параболы.
Свойства параболы:
1)Ох – ось симметрии
2)р>0=>х≥0=> парабола расположена справа от оси Оу
3)При х=0;у=0=> парабола проходит через начало координат.
4)точка О(0;0) – вершина параболы FM=r-фокальный радиус точки М.
Вопрос 17.
Приведение линии 2-го порядка к каноническому виду.
Укажем, как можно с помощью преобразований координат, рассмотренных в предыдущем параграфе, привести общее уравнение кривой второго порядка
к каноническим уравнениям эллипса, гиперболы или параболы, или к случаям их выражения.
С помощью поворота осей координат на некоторый угол α всегда можно избавиться от члена с произведением координат. Действительно, подставляя в (47) вместо x и y их выражения по формуле (43), получим новое уравнение
коэффициент
которого
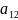будет равен
Приравнивая коэффициент к нулю, получим тригонометрическое уравнение
Отсюда получаем
Далее, по формулам тригонометрии, получаем нужные нам значения для sin α и cos α :
Следовательно, уравнение кривой в новых координатах O'x'y' примет вид:
Если
в уравнении (50)
то говорят, что это уравнение определяет
линию эллиптического типа; если же
то говорят, что уравнение определяет
линию гиперболического типа и, если
один из коэффициентов
или
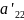равен нулю, то уравнение (50) определяет
линию параболического типа.
Далее с помощью параллельного переноса системы координат O'x'y' уравнение (50) всегда можно привести к виду:
т.е. фактически к каноническому виду.
Из
уравнения (51) следует, что мы имеем либо
эллипс (если
и
одного знака, а
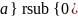противоположного),
либо мнимое место точек (если , , имеют один знак),
либо одну точку (если и имеют один знак, а = 0),
либо гиперболу (если и разных знаков и ≠ 0),
либо две пересекающие прямые (если и разных знаков и = 0).
Если
же в уравнении (50) один из коэффициентов
и
, например,
обращается в нуль, то это уравнение с
помощью переноса осей приведется к
каноническому уравнению параболы
при
≠ 0 или к виду
при
= 0, что дает или две параллельные прямые,
или мнимое место точек.
Отсюда следует, что всякая кривая 2-го порядка есть либо эллипс, либо гипербола, либо парабола, либо представляет собой их "вырождение".