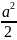Вопрос 13.

Уравнение прямой в пространстве, как пересечение двух плоскостей.

Прямая в пространстве можно рассматривать как прямая пересечения поверхностей(рис) или как геометрическое место точек, общих двум поверхностям.

Если = 0 или = 0 – уравнение двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют система двух уравнений с тремя неизвестными:

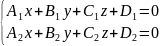
Уравнение системы называется уравнениями прямой в пространстве.

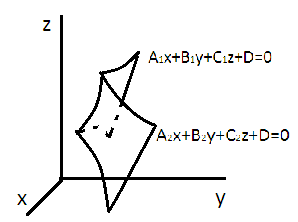
Вопрос 16.

Эллипс. Определение, основные свойства, уравнение и построение.

Эллипсом называется множество всех точек, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называется фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

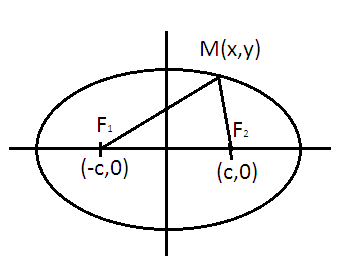
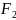Обозначим фокусы через и , расстояние между ними через 2с, а сумма расстояний от произвольной точки эллипса до фокусов – через 2а(рис). По определению 2а>2с, т.е. а>с.

Для вывода уравнения эллипса выберем систему координат Оху ток, чтоб фокусы и лежали на оси Ох, а начало координат совпало с серединой отрезка . Тогда фокусы будут иметь следующие координаты (-с,0) и (с,0)

=2с

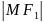+ = conct(2a)

+ >2с

+ =2а

-с= =>

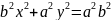или

- эллипс

Свойства эллипса:

1)Если точка (х,у) принадлежит эллипсу, то если ему так же и принадлежат точки (-х,у),(х,-у),(-х,-у), то эллипс симметричен относительно оси Ох, Оу и так же симметричен относительно начало координат

2)Если точки если эти точки пересечения эллипса с осями, то их называют вершинами эллипса, если цент эллипса совпадает с центром координат выше имеются ввиду оси координатные (если центр эллипса смещен от начала координат, то сначала выполняем перенос системы координат, а под осями выше подозреваем оси эллипса) (а оси эллипса проходят через центр эллипса, одна из осей содержит фокусы, вторая ей перпендикулярна)

Отрезки называются осями эллипса

=2а

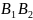=2b

а, b- полуоси эллипса.

3)Из уравнения следует=>

≤1

≤1

-a≤x≤a, -b≤y≤b

Все точки эллипса лежат внутри прямоугольника образованного прямыми

x= a

y= b

4.Из уравнения =>при увеличении х уменьшается у и наоборот.

5.При если a=b, то имеем окружность.

6.Если а большая полуось эллипса, то отношения =έ – называется эксцентриситетом, 0<έ<1

έ= = => =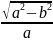

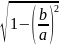Чем меньше έ, тем эллипс будет менее сплющенным. Если эллипс равен нулю, то имеем окружность.

7) если точка М(х,у) € эллипсу, то M и M называют фокальными радиусами

M=a+έх

M=a-έх

8) х=

Вопрос 17.

Гипербола. Определение, основные свойства, уравнение и построение.

Гипербола – это геометрическое место точек плоскости разности расстояний от каждой, из которой до двух данных точек плоскости называемые фокусами, есть величина постоянная и меньшая чем расстояние между фокусами.

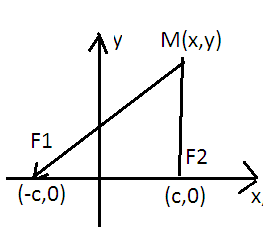
Пусть и фокусы расстояние =2с, а модуль разности расстояний, от произвольной точки M гиперболы до фокуса 2а<2с=>а<с введем в систему координат хОу так чтобы и лежали на координатной оси симметрично относительно началу координат

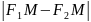=2а

M- M= 2а=> – =2а=> 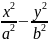=1 – каноническое уравнение(9)

При этом

Свойства гиперболы:

1.Уравнение содержит х и у в четных степенях, то гипербола симметрична относительно координатных осей и начало координат.

2. - точки пересечения гиперболы с осью Ох, точек пересечения с осью Оу гиперболы не имеет.

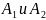- вершины гиперболы, отрезок =2а- действительная ось гиперболы отрезок = =а – полуось гиперболы, отрезок =2b, где =(0,b) мнимая ось гиперболы, отрезок =b –мнимая полуось гиперболы, прямоугольник со сторонами равными 2а и 2b для которого точки , , -являются центрами его сторон основной прямоугольник гиперболы.

3.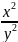 ≥1=> 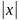≥а , следовательно точки гиперболы расположены справа от прямой х=а (правая ветвь гиперболы) и слева от прямой х=-а(левая ветвь гиперболы)

4.Из того что величина постоянная следуют, что гипербола имеет форму кривой состоящей из двух ветвей.

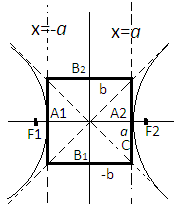
5.Опредениение. Прямая линия L называется асимптотой не ограниченной кривой k, если расстояние d, от точки М кривой k до этой прямой L стремимся к нулю, при неограниченном удаление точки М вдоль кривой k от начала координат.

Гипербола задаваемая уравнением (9) имеет две асимптоты у=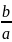 х и у= х

6.έ= 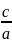-эксцентриситет гиперболы, если a – действительная ось, =>έ>1 чем меньше отношения тем более вытянут её основной прямоугольник.

7.

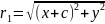
– фокальные радиусы гиперболы.

8.Прямые х - директрисы гиперболы расположенные между центром и вершиной параболы.

9. - =1 – уравнение гипербола с действительной осью 2b

10.Если а=b, то гипербола называется равно сторонней, если асимптотами не является оси координат, то её уравнение имеет вид.

у=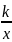

k=